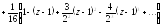- •Содержание Двойной и тройной интегралы.
- •1 Двойной интеграл. Объем цилиндрического тела.
- •2 Свойства двойных интегралов
- •3 Вычисление двойного интеграла
- •4 Двойной интеграл в полярных координатах
- •5 Вычисление площади поверхности
- •6 Вычисление площадей и объёмов посредством двойного интеграла
- •7. Тройной интеграл
- •8. Физические приложения двойных и тройных интегралов
- •Криволинейные интегралы первого и второго рода.
- •1 Криволинейный интеграл второго рода по координатам
- •2 Вычисление криволинейного интеграла по координатам
- •3 Криволинейный интеграл первого рода (по длине дуги)
- •4 Основные свойства криволинейного интеграла первого рода
- •5. Формула Грина.
- •7 Поверхностные интегралы
- •8 Вычисление поверхностного интеграла
- •9 Формула Стокса
- •Элементы теории поля.
- •1 Скалярное поле. Производная по направлению. Градиент
- •2 Векторное поле. Поток и дивергенция поля
- •3 Циркуляция и ротор векторного поля
- •4. Оператор Гамильтона и его применение.
- •Дифференциальные уравнения
- •1. Основные понятия. Дифференциальные уравнения с разделяющимися переменными.
- •2. Однородные уравнения
- •5. Интегрирование дифференциальных уравнений высших порядков.
- •6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
- •7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
- •8. Уравнение Эйлера
- •9. Линейные системы дифференциальных уравнений с постоянными коэффициентами
- •Теория функций комплексного переменного.
- •1. Комплексные числа
- •2. Непрерывные функции комплексного переменного
- •3. Дифференцирование функций. Условие Коши-Римана.
- •4 Сопряжённые гармонические функции
- •5 Конформное отображение
- •6 Постоянство растяжений
- •7 Интеграл по комплексному переменному
- •8 Ряд Лорана
- •9 Классификация изолированных особых точек
- •10 Вычеты
- •11. Вычисление интегралов при помощи вычетов
- •12. Вычисление интегралов, содержащих показательную функцию
- •13. Задачи по Теории Функции Комплексного Переменного
11. Вычисление интегралов при помощи вычетов
Теорема 1.
Пусть
 удовлетворяет перечисленным условиям
и кроме того
удовлетворяет перечисленным условиям
и кроме того
 при
при
 ,
а
,
а - достаточно большое число.
- достаточно большое число.
Тогда

Доказательство.
Опишем
полуокружность ориентированную против
часовой стрелки радиуса
 .
.



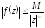 ,
при
,
при
 ,
то
,
то при
при
Теорема 2.
Пусть
функция
 удовлетворяет условиям, отмеченным в
начале и
удовлетворяет условиям, отмеченным в
начале и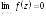 ,
тогда
,
тогда
Пример 1.
Найти
вычеты функции
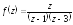 .
.


Пример 2.

 - полюс третьего
порядка
- полюс третьего
порядка

Пример 3.

Имеется
устранимая особенность в точке

 ;
;

Пример 4.
 ;
;
 - аналитична в верхней полуплоскости,
кроме точек
- аналитична в верхней полуплоскости,
кроме точек
 ;
;
 ;
;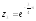 ;
;








Пример 5.

Полюсами
являются корни уравнения
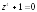 ,
которые лежат внутри окружности
,
которые лежат внутри окружности .
.



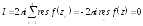
Теорема.
Если
 имеет в расширенной комплексной плоскости
конечное число особых точек, то сумма
всех её вычетов, включая вычет в
бесконечности равна нулю.
имеет в расширенной комплексной плоскости
конечное число особых точек, то сумма
всех её вычетов, включая вычет в
бесконечности равна нулю.
12. Вычисление интегралов, содержащих показательную функцию
Интегралы Френеля (1788-1827)
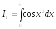








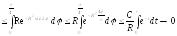 ,
,
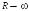





13. Задачи по Теории Функции Комплексного Переменного
Найти действительные решения уравнений.
1)



 ;
;
 ;
; ;
;
 ;
;

2)


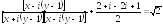

3)

 ;
;

Найти модуль и аргумент комплексного числа.
1)

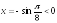





2)


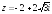

Тригонометрическая и показательная формы комплексного числа





Записать в тригонометрической форме.
1)





2)

 ;
;
 ;
;

Показательная.



Вычислить





Найти
все значения



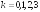

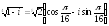



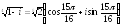


Написать в комплексной форме уравнение прямой.










Написать в комплексной форме уравнение окружности.






Какая линия на плоскости определяется следующим уравнением


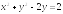

Центр
окружности


Вычислить
 с точностью до 0,001
с точностью до 0,001


Решить
уравнение







Условие Коши-Римана
 ;
;


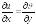 ;
;


Дифференцируема ли

 =0
=0
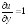

 Данная функция
не дифференцируема.
Данная функция
не дифференцируема.
2)



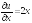


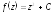
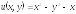
 - дифференцируема
- дифференцируема









Формула вычисления интеграла

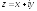

Пример 1.
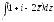
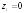 ;
;
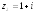

1.
Прямая






2.
Парабола



Пример 2.





 ;
;


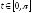



Пример 3.


Пример 4.


Интегральная форма Коши.
Если
 является аналитической в области
является аналитической в области ,
ограниченной кусочнозамкнутой прямой
,
ограниченной кусочнозамкнутой прямой
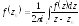 ,
где
,
где

Пример.
 ,
т.к. у нас имеются особые точки
,
т.к. у нас имеются особые точки
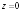 и
и ,
которые не входят в данную область
,
которые не входят в данную область
окружность

Пример.

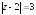

Пример.
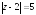
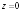

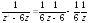

Пример.
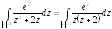


Ряд Тейлора. Ряд Лорана
Разложить
в ряд Тейлора в окрестности точки



Ближайшей
к
 особой точкой данной функции является
особой точкой данной функции является поэтому радиус сходимости
поэтому радиус сходимости .
.
Разложить
по
 функцию
функцию
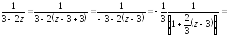




Найти
область сходимости ряда

 ;
;
 ;
;


Разложить
в ряд Лорана
 в кольце
в кольце