8 Ряд Лорана

Теорема 1.

Пусть .

Всякая аналитическая функция в кольце (1) однозначна и представлена в виде сходящегося ряда

(2)

(3)

;

Ряд (2) называется рядом Лорана функции по степеням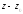или разложением Лорана функции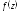в кольце (1).

Когда полагаем, что сходится, то подразумевается, что сходятся отдельнои

Пример.

Функция 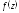аналитическая на плоскости за исключением точек 2 и 3.

a) Функция 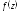аналитична в кругеи на основании теоремы её можно разложить в ряд Тейлора по степенямсходящимся в круге

;

b) Функция 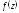аналитическая в кольце

- окружность ориентирован против часовой стрелки.

Для

c) Функция аналитична во внешней области кругаи удовлетворяет неравенству.

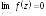
можно разложить в ряд Лорана

Элементы не могут входить в разложение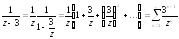

Пример.

Разложить в ряд Тейлора по степеням

- открытый круг с центром в точке радиуса.

Внутри аналитическая, а любой больший его концентрический круг содержит в себе особую точку, в которой аналитичность нарушается. Разложимв ряд Тейлора по степеням

Вывод:

Искомая функция есть разложение в ряд Тейлора по степеням функции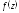. Радиус сходимости этого ряда.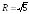

9 Классификация изолированных особых точек

Пусть ианалитична в кольце, то она раскладывается на сходящийся в ней ряд Лорана.

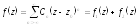
Пусть предполагается, что функция аналитическая во внешнем круге, из которого выколота точка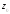

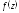В точке функция бывает неопределенна, в этом случае- изолированная особая точка. Степенной рядимеет радиус сходимостипоэтому его производная непрерывна в круге

Первый случай.

Т.к. степенной ряд сходится для любого , то его радиус сходимости равен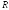и его суммаопределена и непрерывно дифференцируема во всех точках круга. Т.о. функцияаналитична в этом круге. Если принять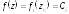, то функциябудет аналитичной. В этом случае особенностьв точкеустранима. Достаточно положить, как функциястанет аналитической не только поблизости от точки, но и в самой точке.

для любого замкнутого контура содержит точкуи принадлежащего кругу.

Второй случай.

Т.к. для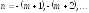

В этом случае полагают, что точка 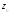есть полюс функциипорядка (кратности). Приточкуназывают простым полюсом.

Т.к. и

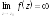
Если - контур, ориентированный против хода часовой стрелки и принадлежащий кругу, то

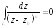
Третий случай.

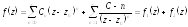
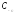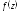В ряду не равно нулю бесконечное число коэффициентов. Считается, чтоимеет в точкесущественную особенность.

Однако в указанных условиях не стремится прик какому-либо пределу.

Пример.

Здесь имеется существенная особенность в точке . Эта функция не имеет предела в точке.- существенно особая точка.

10 Вычеты

Пусть - полюс-го порядка функции. Вычет функцииотносительно её полюса-го порядка вычисляется по формуле

Если - полюс 1-го порядка

При вычислении вычета в точке

(ряд Лорана)

Теорема о вычетах.

Пусть аналитическая на всей плоскостиза исключением конечного числа точек. Тогда

Доказательство.

Построим окружности ориентированные по часовой стрелке с центрами соответствующие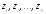настолько малого радиуса, чтобы они не пересекались. Кроме того, построим окружностьориентированную против часовой стрелки с центром в нулевой точке настолько большого радиуса, чтобы она охватывала все окружности.

Сложный контур ограничивает областьв которой функцияаналитическая.

При обходе по 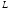областьостаётся слева, тогда на основании теоремы Коши для сложного контура

(*)

или

Внутри каждого из контуров 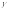находится одна особая точка, а вне контура только одна особая точка.

Вывод:

Если затруднительно вычислить интегралы из (*).

Само вычисление этих интегралов сводится к разложению 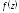в ряд Лорана в окрестности соответствующих особых точек.