1. Декартовы тензоры и тензорные обозначе­ния

Тензорные обозначения широко используют в механике сплошных сред. Они по­зволяют упростить запись величин и выражений и сделать их более яс­ными.

Декартовы координаты прямоугольной системы координат ,,обозна­чают че­рез,,и записывают их как, где индекспринимает значения 1, 2, 3 (рис. 1). Тогда,,.

Вместо индекса можно взять другую латинскую букву, например. То­гда имеем.

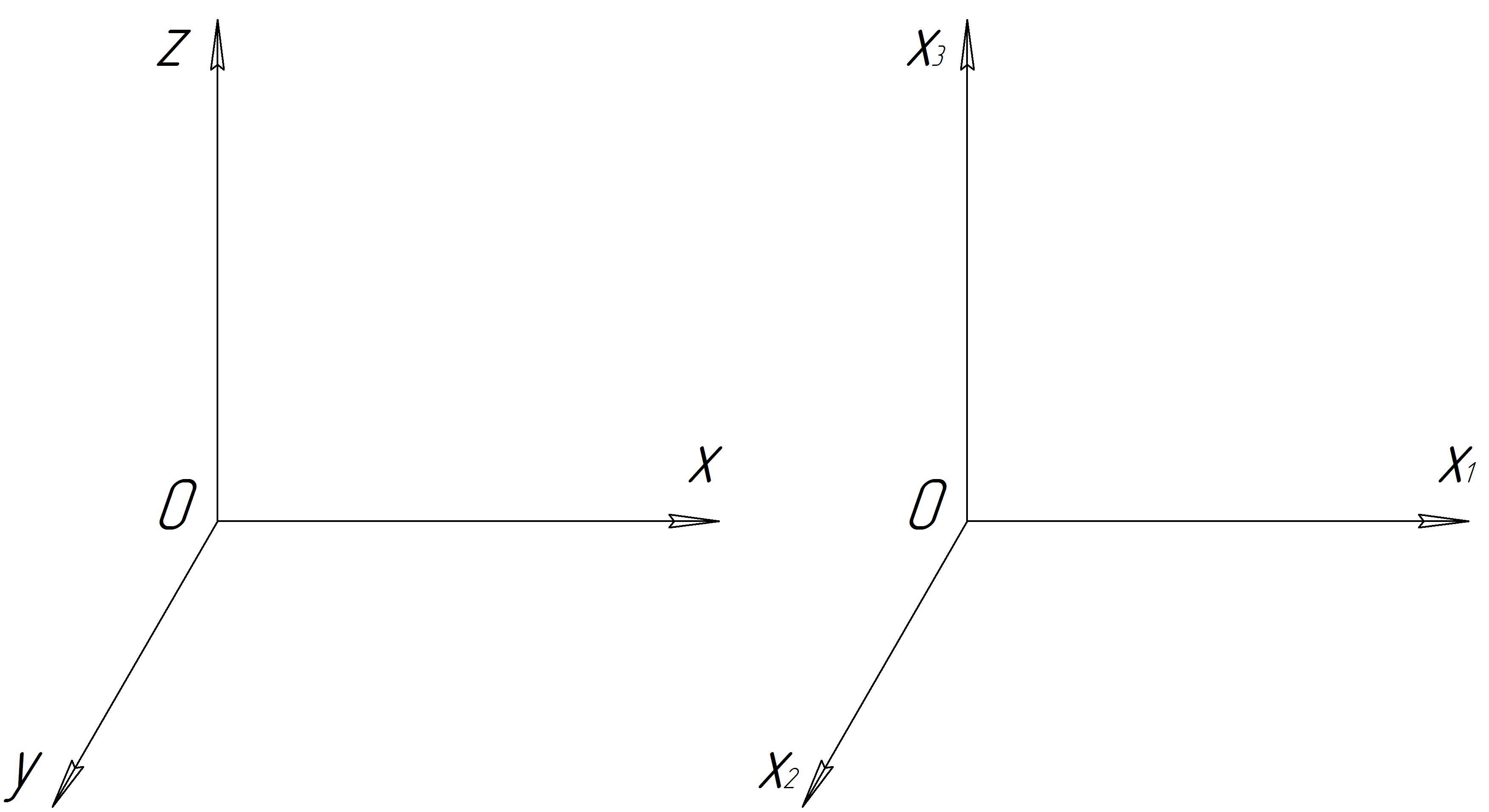
Рис. 1

Широкое распространение получило правило суммирования, введенное А. Эйн­штейном. Согласно этому правилу по всякому дважды повторяющемуся в од­ночлене ла­тинскому индексу проводится суммирование по значениям 1, 2, 3, а знак суммы опуска­ется, т.е.

.

Эта запись является равносильной записи

.

Повторяющийся индекс называется немым. В каждом одночлене он не должен встречаться более двух раз. Если немой индекс заменить другой буквой, то сумма не ме­няет своего значения:

.

Неповторяющиеся индексы называются свободными. В одночлене ин­декс- свободный,- немой.

В тензорных обозначениях широко используют символ Кронекера (единич­ный тен­зор):

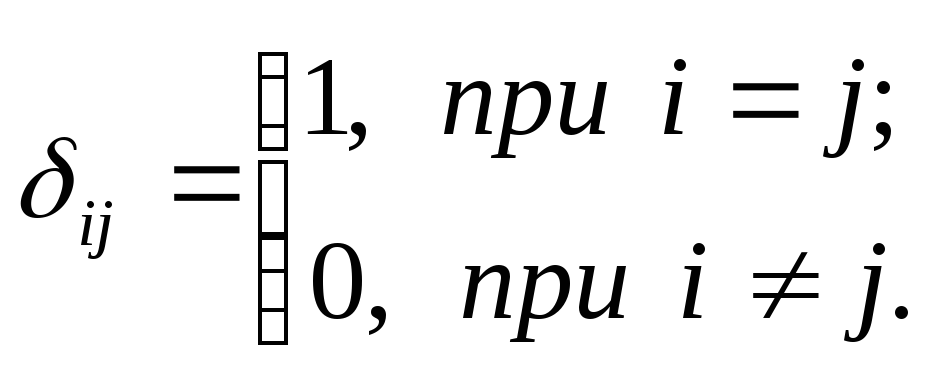
Вектор в трехмерном пространстве характеризуется тремя компонентами,,и описывается тензором первого ранга. При изменении системы коорди­нат компо­ненты преобразуются по формуле

, (1)

где - компоненты вектора в новой системе,

- компоненты вектора в старой системе,

- косинусы углов между старой и новой системами координат.

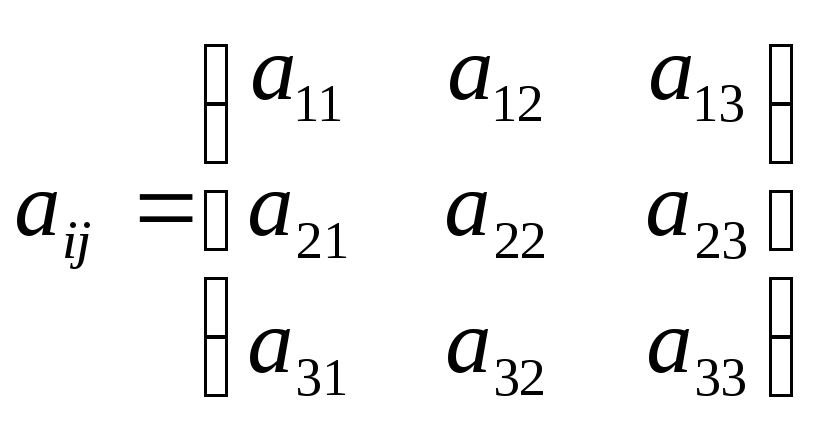
Компоненты тензора второго ранга можно обозначить через ,.

Соотношения между тензорными обозначениями и использованными выше обо­значениями координат через ,,очевидны:

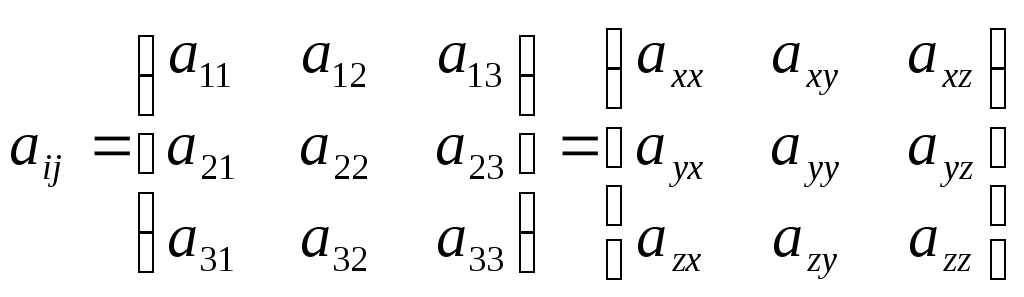
Компоненты тензора второго ранга преобразуются по следующему закону:

, (2)

где - компоненты тензора в новой системе,

- компоненты тензора в старой системе,

, - косинусы углов между старой и новой системами координат.

В индексных обозначениях ранг тензора определяется только свободными индек­сами, например - тензор первого ранга,- тензор второго ранга,- тензор четвер­того ранга.

Над тензорами можно проводить ряд операций:

1. Два тензора одинакового ранга равны, если равны их соответствующие компо­ненты .

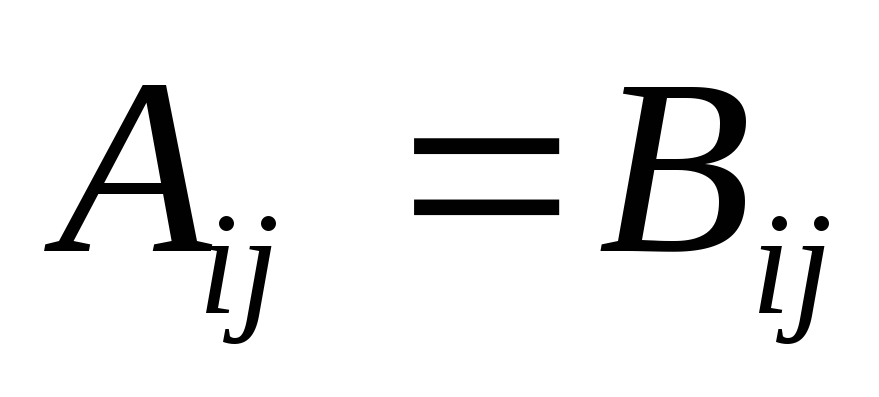2. Умножение тензора на скаляр дает новый тензор того же ранга.

3. Тензоры одинакового ранга можно складывать или вычитать покомпонентно .

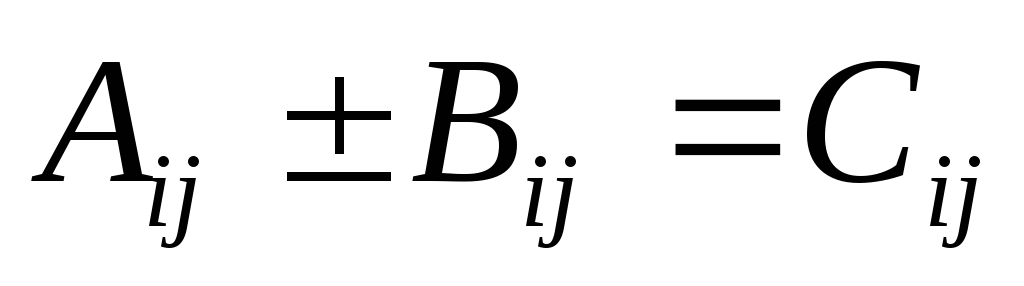Число компонент тензора подчиняется выражению , гдеN – число компонент, а Р – ранг тензора.

Задачи

1. Даны два симметричных тензора второго ранга:

, .

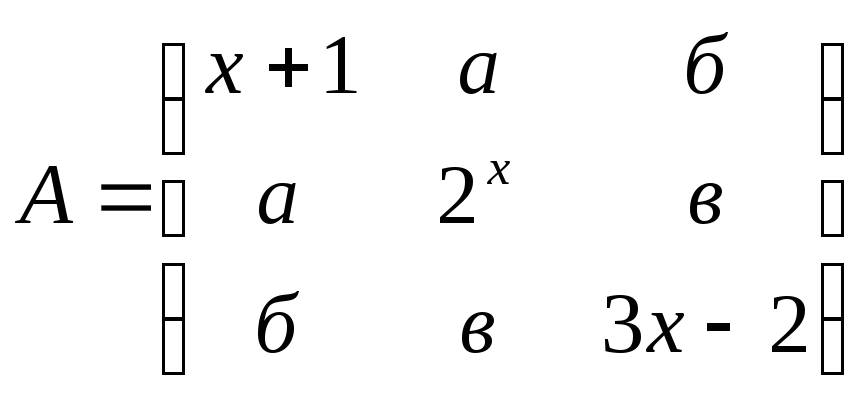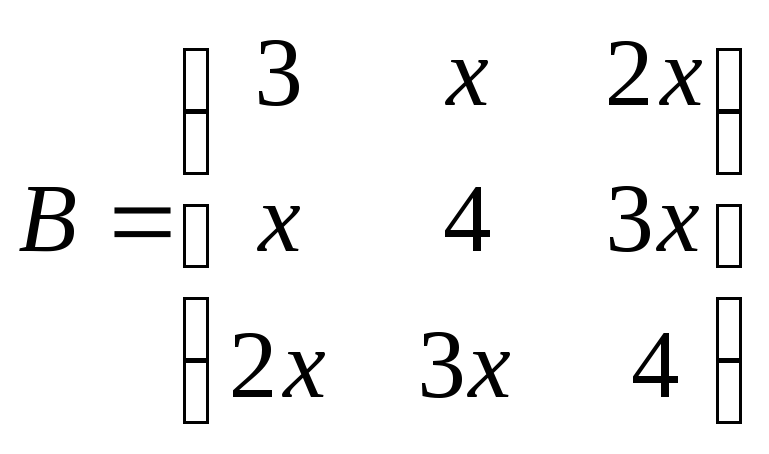При каком значении тензоры A и B равны между собой? Чему при этом равны а, б, в?

2. Записать в развернутой форме статические уравнения равновесия сил

.

Решение. Индекс - немой, принимает все возможные значения 1,2,3 и по нему проводим суммирование. Если выбрано и зафиксировано определенное на­правление, то индекс не меняется. Например, если выбрано направление, то везде. В декарто­вой системе координат, в то время как пробегает значения ,,. Приняв после­довательно, получим уравнения равнове­сия сил для всех направлений:

:,

:,

:,

или в декартовых координатах:

,

,

.

3. В трехмерном пространстве расшифровать уравнение

.

Решение. В одночлене два немых индекса и . Следовательно прово­дится двой­ное суммирование:

,

.

В начале провели суммирование по индексу (), затем по индексу ().

4. Записать в развернутой форме следующие тензорные символы:

, ,,.

5. Найти значения выражений, содержащих символ Кронекера:

, , , , , .

6. Записать в развернутом виде:

, .

7. Известно, что составляющие полного напряжения на наклонной площадке в прямо­угольной системе координат 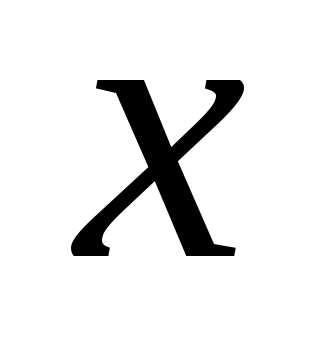,,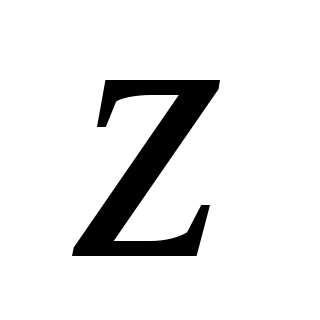записываются следующим образом (уравне­ния Коши):

,

,

.

Записать их в тензорном обозначении.

Решение. Из последнего равенства видно, что индекс "" относится ки стоит пер­вым в обозначении напряжений. Предположим, что мы обозначили его через "". Второй индекс входит в выражение напряжений и направляющих косину­сов. Обозначим его "". Следовательно, в тензорном обозначении указан­ные уравнения можно представить так:

.

Таким образом, при ,.

8. Нормальное напряжение на наклонной площадке записывается в виде

или

.

Дать тензорную запись этих уравнений, приняв ,,.

9. Первый и второй инварианты тензора напряжений имеют вид

,

.

Представить их в тензорном обозначении.

10. Представить следующие формулы в тензорном обозначении:

,

,

.

11. Определить ранг тензорных величин

, ,,.

12. В системе координат 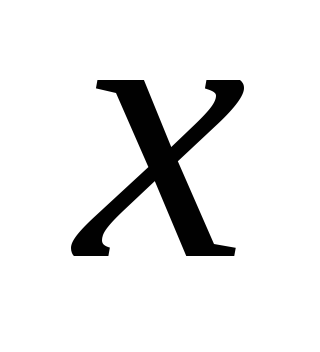,,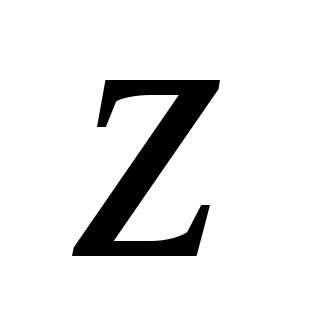задан вектор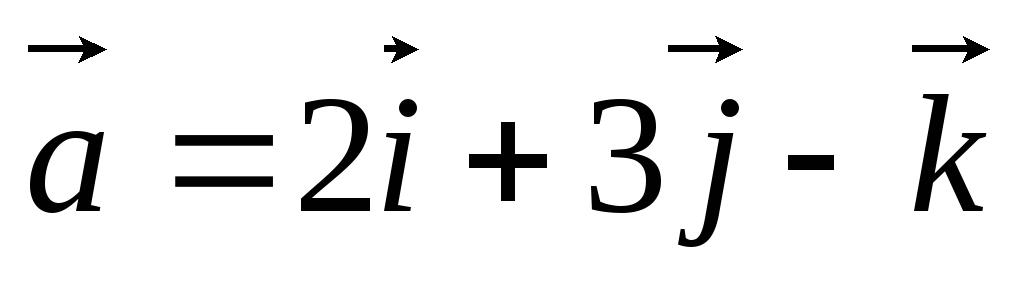. Определить его компо­ненты в новой системе координат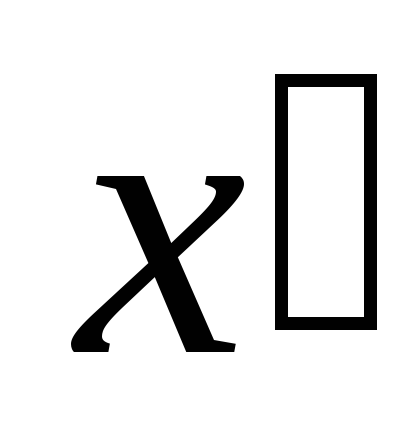,,, 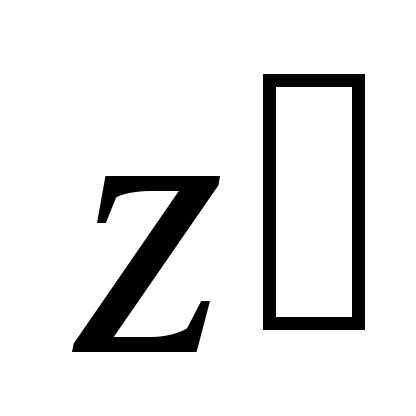направление осей которой задано табл.1 направляющих косинусов:

Таблица 1

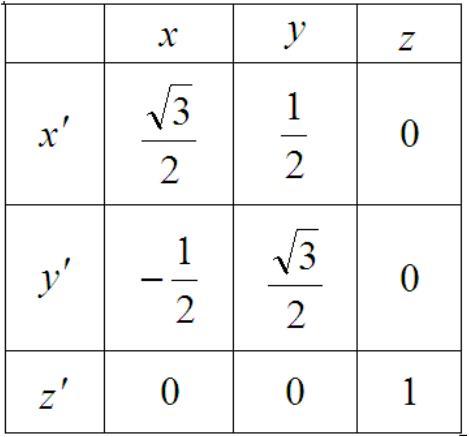
Решение. На основании формулы (1) имеем:

,

,

.

В системе координат ,,вектор записывается следующим образом:

.

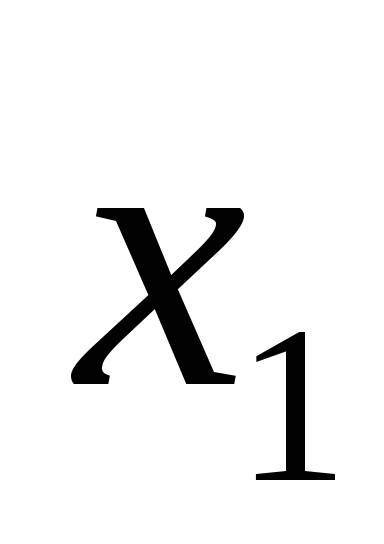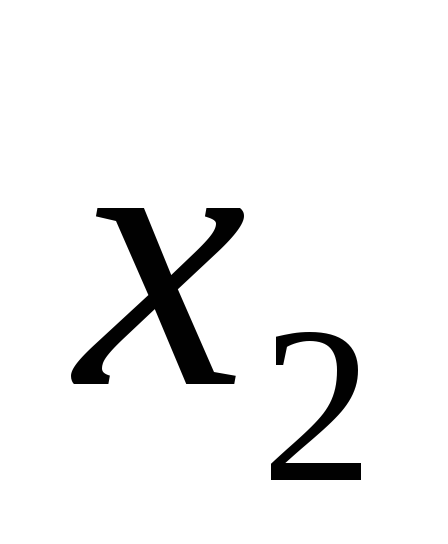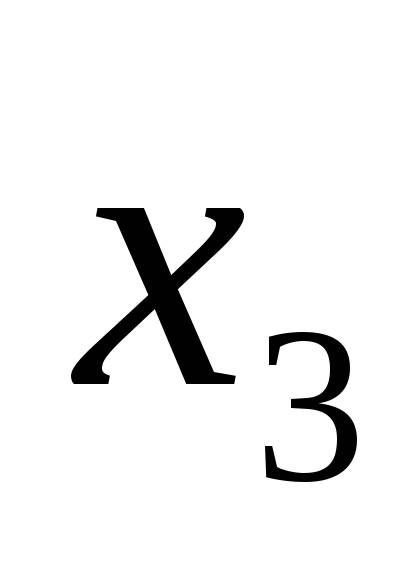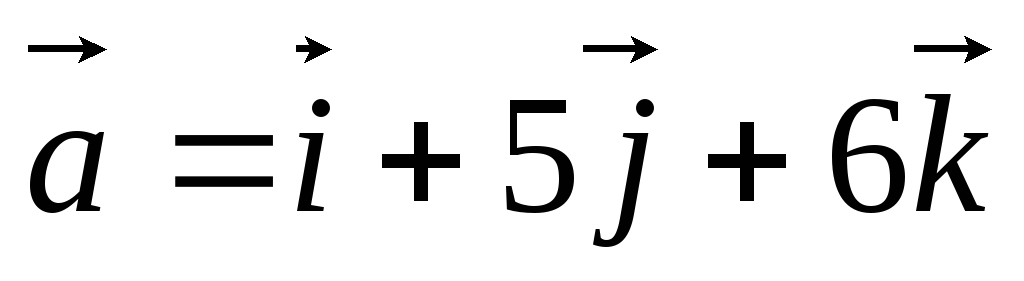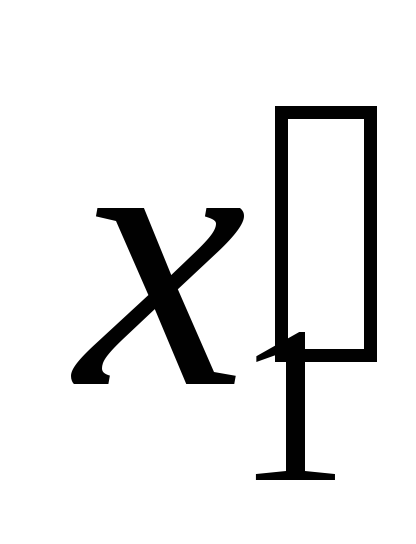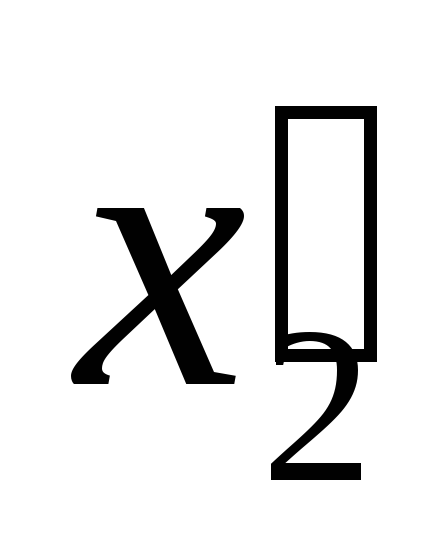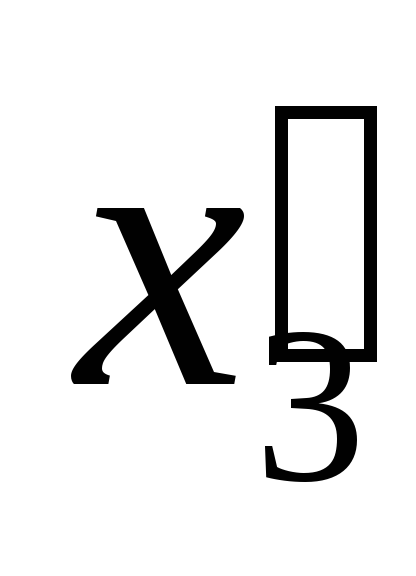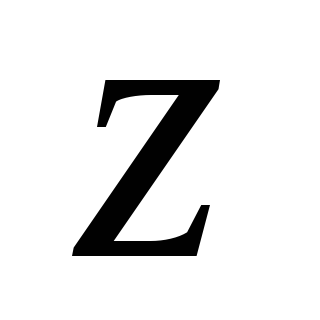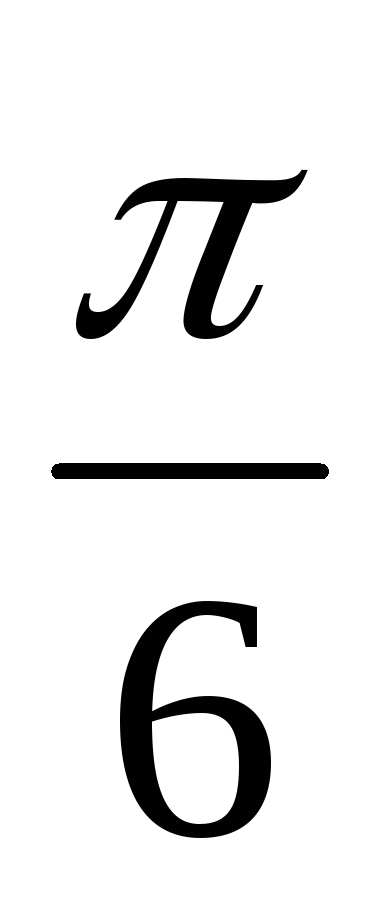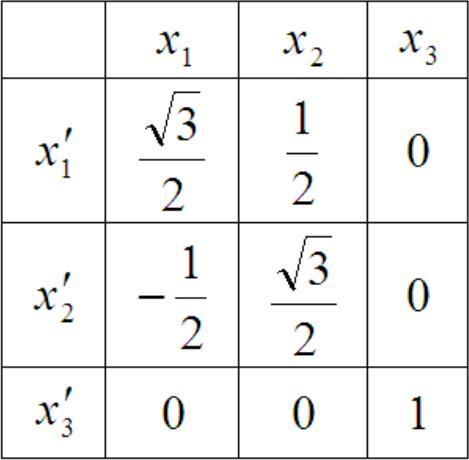
13. В системе координат ,,задан вектор. Определить ком­по­ненты в новой системе координат,,, полученной поворотом вокруг осина угол. Табл.2 направляющих косинусов имеет вид:

Таблица 2

14. Для тензора второго ранга

.

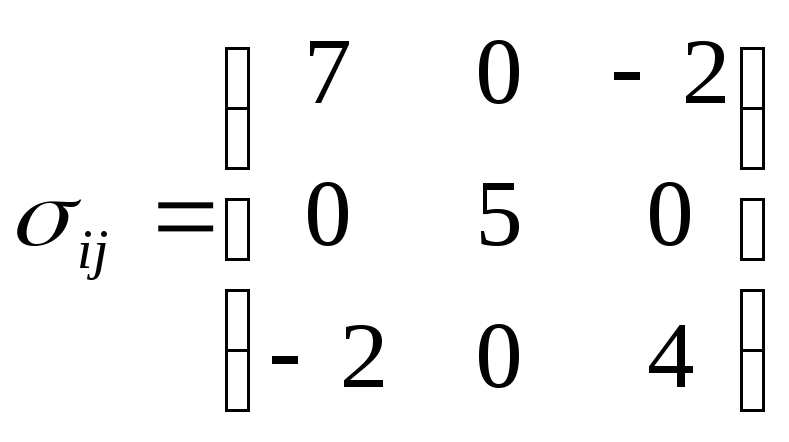Определить компоненты в системе координат,,, заданной табл.3 направляю­щих косинусов.

Таблица 3

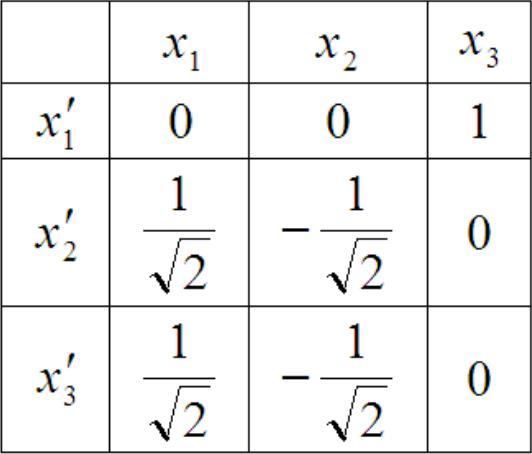
Решение. По формуле (2):

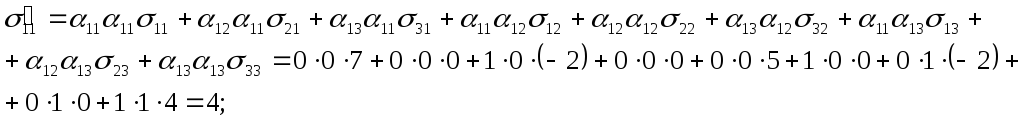
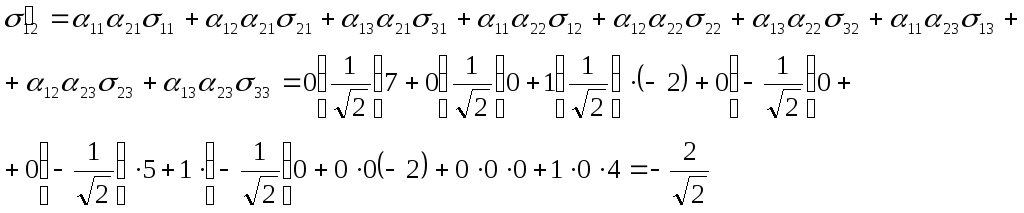
и т.д.

В результате

.

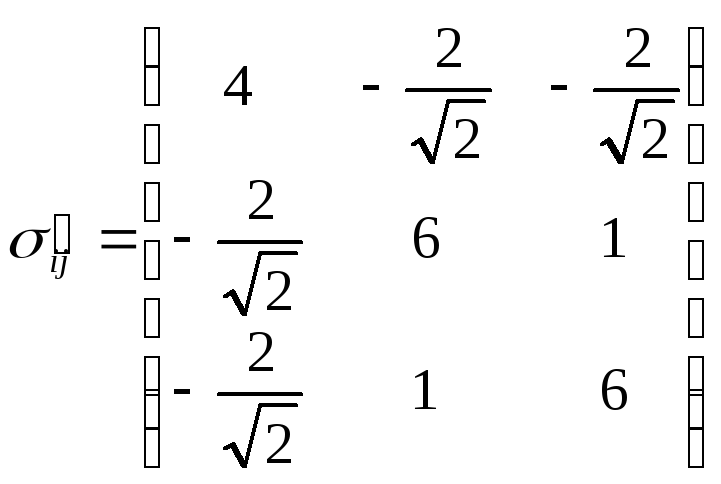15. В системе координат 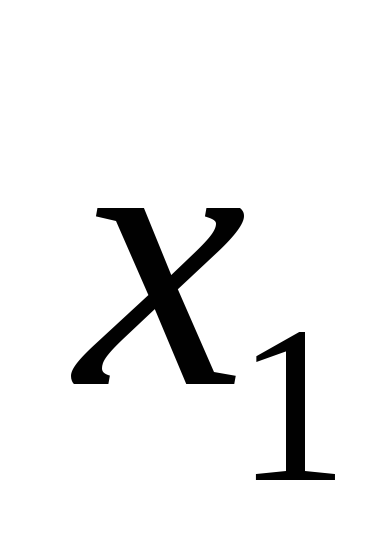,,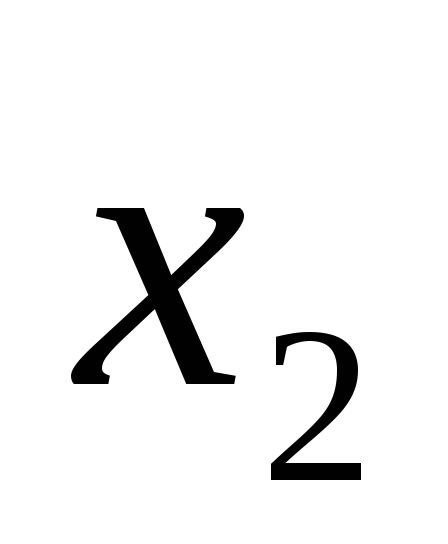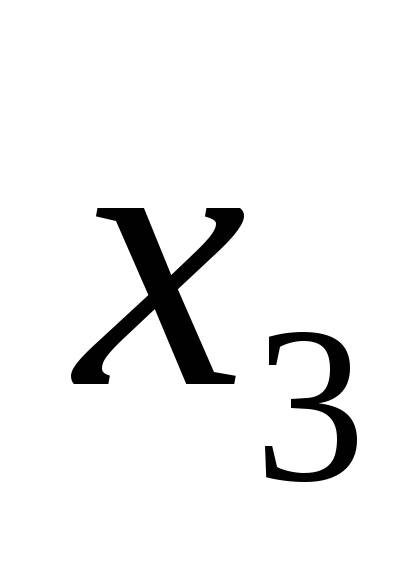задан симметричный тензор второго ранга:

,

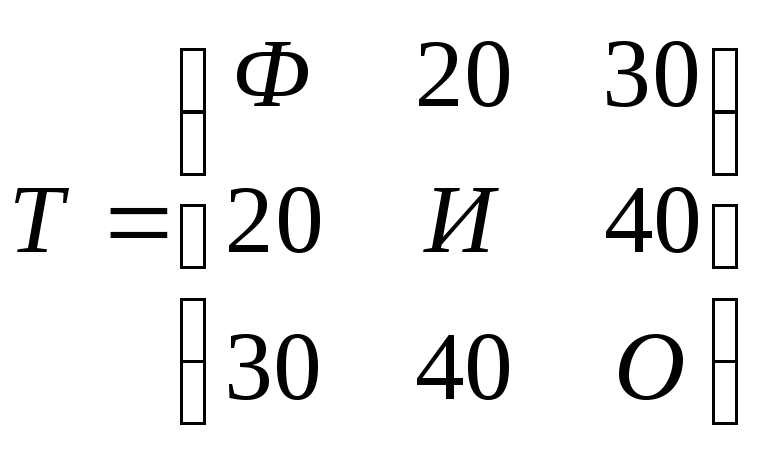где по главной диагонали Ф – число букв в фамилии, И – число букв в имени, О – число букв в отчестве сту­дента.

Определить его компоненты в новой системе координат ,,, получен­ной пово­ротом вокруг осина угол, направление осей которой задано табл.2 направляю­щих косинусов в задаче 1.13.