
- •В.Ю. Арышенский, в.Р. Каргин, б.В. Каргин
- •Isbn 978-5-7883-0679-7
- •Оглавление
- •Основные условные обозначения
- •Декартовы тензоры и тензорные обозначения
- •Напряженное состояние в окрестности заданной точки
- •Главные нормальные и касательные напряжения. Октаэдричиские напряжения.
- •Разложение тензора напряжений
- •Круги мора для напряжений
- •Деформированное состояние тела
- •Основные уравнения теории упругости
- •Плоские и осесимметричные задачи теории упругости
- •Удельная потенциальная энергия
- •Условие пластичности и наступление
- •Применение теории пластичности
- •Приложение
- •Единицы
- •Международной системы си в задачах
- •По механике сплошных сред
- •Арышенский Владимир Юрьевич
Применение теории пластичности
Энергетическое условие пластичности может быть представлено в линейном виде:
тело изотропное
![]() ,
,
где
![]() ;
;
![]() –коэффициент
Лоде лежит в пределах от
–коэффициент
Лоде лежит в пределах от
![]() до
до![]() ;
;
тело ортотропное
![]() ,
,
где
 ;
;
![]() ;
;
![]() .
.
Интенсивность деформаций (при условии постоянства объема) в случае изотропного тела может быть получена по формуле
![]()
или
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() – логарифмические деформации.
– логарифмические деформации.
Если тело является ортотропным, то
 .
.
При плоском напряженном состоянии физические уравнения имеют вид:
тело изотропное
![]() ,
,
![]() .
.
тело ортотропное
![]() ,
,
![]() .
.
Задачи
Стальной толстостенный цилиндр находится под действием внутреннего давления
 .
Определить предел пластического
сопротивления, т.е. то наименьшее
давление
.
Определить предел пластического
сопротивления, т.е. то наименьшее
давление ,
при котором весь металл перейдет в
пластическое состояние (тело принять
изотропным). Для численного решения
использовать данные задачи 10.7.
,
при котором весь металл перейдет в
пластическое состояние (тело принять
изотропным). Для численного решения
использовать данные задачи 10.7.Определить предел текучести пластического сопротивления стального цилиндра в случае цилиндрической анизотропии. Для численного решения использовать данные, приведенные в задаче 10.8.
В задаче 11.1 изменить условие, считая, что действует и наружное давление
 .
Рассмотреть два случая:
.
Рассмотреть два случая: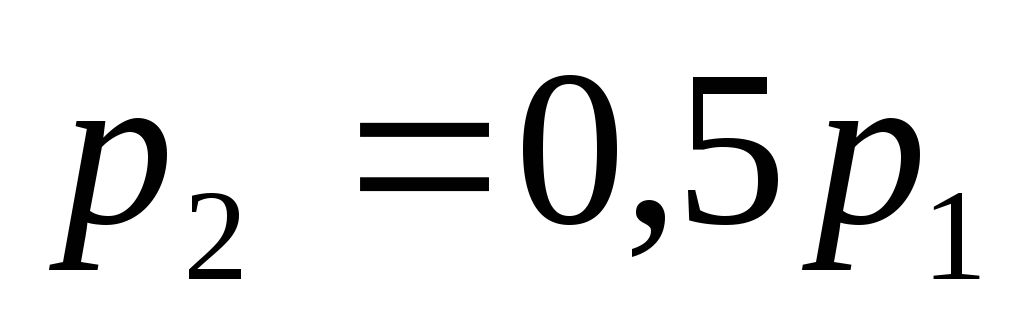 и
и .
.Нанесенная на свободную поверхность листовой заготовки круглая ячейка делительной сетки диаметром
 на конечном этапе деформирования
превратилась в эллипс, главные диаметры
которого соответственно равны
на конечном этапе деформирования
превратилась в эллипс, главные диаметры
которого соответственно равны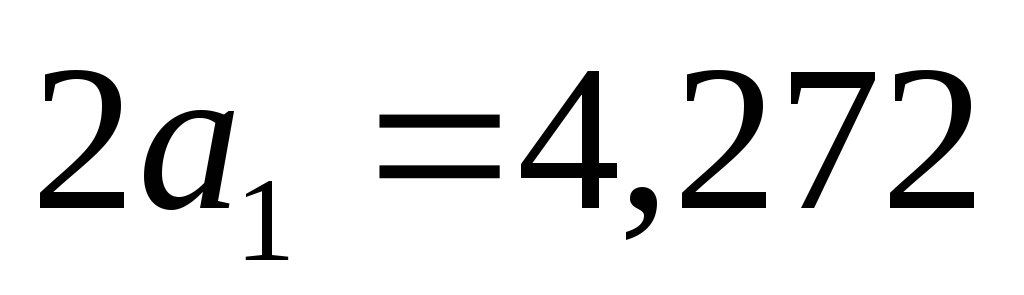 ;
; .
Использовав уравнение кривой упрочнения
.
Использовав уравнение кривой упрочнения ,
определить главные компоненты
напряжения. Процесс деформирования
считать монотонным.
,
определить главные компоненты
напряжения. Процесс деформирования
считать монотонным.
Решение. Определим значения главных логарифмических деформаций:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Интенсивность логарифмических линейных деформаций найдем по формуле
![]()
Интенсивность нормальных напряжений рассчитываем по уравнению кривой упрочнения
![]() .
.
Поскольку
сетка нанесена на свободную поверхность,
то напряжение, нормальное поверхности
листа
![]() ,
является главным и равно нулю. Для
определения остальных главных компонент
напряжений воспользуемся соотношением
Гука – Генки:
,
является главным и равно нулю. Для
определения остальных главных компонент
напряжений воспользуемся соотношением
Гука – Генки:
![]() ;
;
![]() ,
,
отсюда следует
![]()
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
На поверхность листа из сплава ОТ4-1 (см. табл.10) была нанесена координатная сетка в виде кругов
 мм.
После деформации листа круги сетки
превратились в эллипсы с размерами
главных осей
мм.
После деформации листа круги сетки
превратились в эллипсы с размерами
главных осей мм
и
мм
и мм.
Кривая истинных напряжений
аппроксимируется степенной функцией
мм.
Кривая истинных напряжений
аппроксимируется степенной функцией ,
где
,
где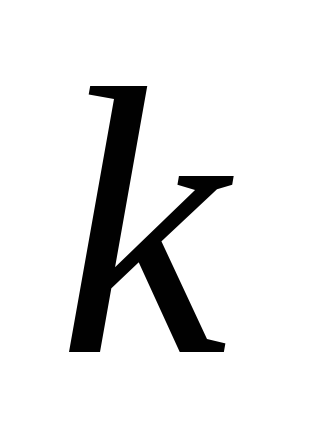 и
и – константы материала. В данном
случае
– константы материала. В данном
случае ,
а
,
а МПа.
Считая, что главные оси деформации
совпадают с осями эллипса, определить
значение компонент напряжений и
деформации (
МПа.
Считая, что главные оси деформации
совпадают с осями эллипса, определить
значение компонент напряжений и
деформации ( принять равным нулю). Как изменяются
полученные результаты, если не
учитывать анизотропию материала?
принять равным нулю). Как изменяются
полученные результаты, если не
учитывать анизотропию материала?Известно, что при гидростатическом выпучивании листовых материалов в центре лунки
 .
Провести сравнение интенсивностей
деформаций и напряжений изотропного
материала, трансверсально-изотропного
сплава (например, ОХ18Н9Т) и одного
из ортотропных листов. Данные по
коэффициенту поперечной деформации
взять из таблицы 10.
.
Провести сравнение интенсивностей
деформаций и напряжений изотропного
материала, трансверсально-изотропного
сплава (например, ОХ18Н9Т) и одного
из ортотропных листов. Данные по
коэффициенту поперечной деформации
взять из таблицы 10.Определить значение коэффициента Лоде
 для материалов, указанных в таблице.
Рассмотреть случае, когда
для материалов, указанных в таблице.
Рассмотреть случае, когда ,
, ,
,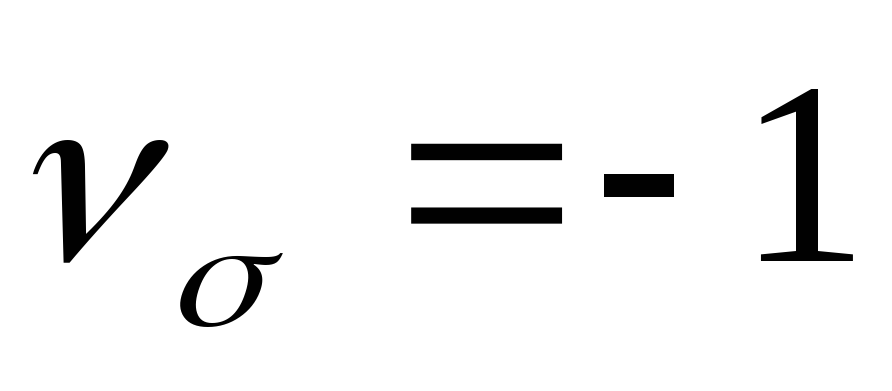 .
.Тонкостенная труба (
 мм)
из алюминиевого сплава с внешним
диаметром
мм)
из алюминиевого сплава с внешним
диаметром мм
подвергалась растяжению и внутреннему
давлению так, что все время сохранялось
следующее равенство между напряжениями:
мм
подвергалась растяжению и внутреннему
давлению так, что все время сохранялось
следующее равенство между напряжениями: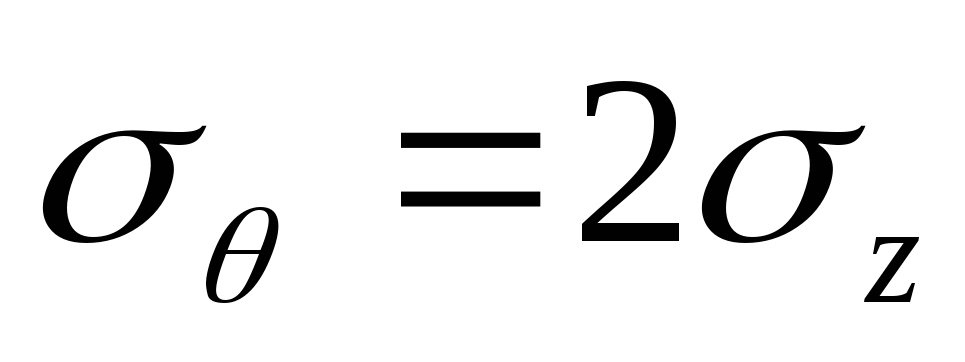 .
Деформация проводилась вплоть до
конечного осевого напряжения
.
Деформация проводилась вплоть до
конечного осевого напряжения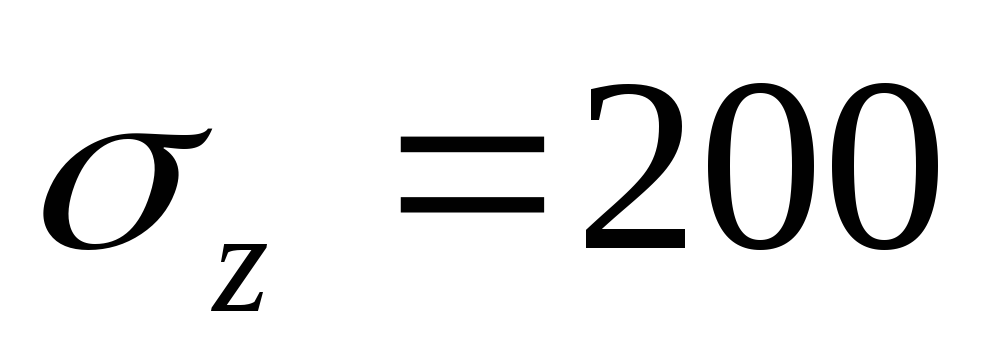 МПа.
Принимая материал трансверсально-изотропным
(
МПа.
Принимая материал трансверсально-изотропным
( )
и коэффициенты степенной аппроксимации
)
и коэффициенты степенной аппроксимации ,
, МПа,
определить конечные размеры трубы.
МПа,
определить конечные размеры трубы.Найти связь между напряжениями и деформациями в пластической области, когда
 .
Рассмотреть три случая:
.
Рассмотреть три случая:материал принят изотропным;
тело является трансверсально-изотропным;
среда – ортотропная.
Упрочнение
материала аппроксимировано степенной
функцией
![]() .
.
Длинная толстостенная труба находится под давлением. Определить напряженно-деформированное состояние и размеры трубы после деформации, если известно:
внутреннее давление
 (
( );
);внешнее давление
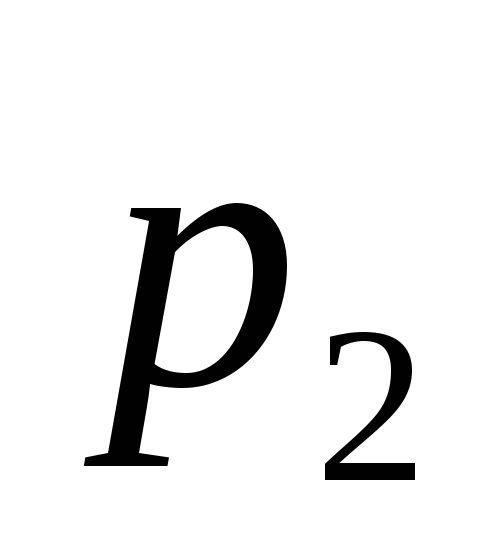 (
(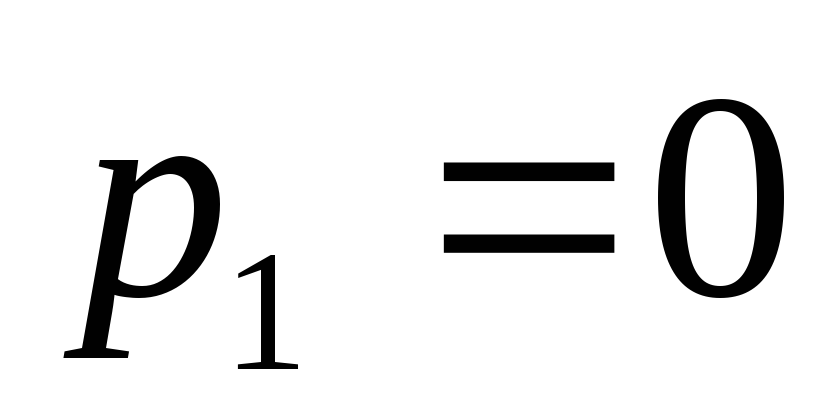 ).
).
Материал трубы (несжимаемый) последовательно принять изотропным, трансверсально-изотропным и ортотропным. Упрочнение принять по степенному закону.
Определить напряженно-деформированное состояние в длинной толстостенной трубе, а также внутреннее давление
 ,
если известно изменение радиуса
,
если известно изменение радиуса .
Рассмотреть два случая:
.
Рассмотреть два случая: и
и .
.
Материал трубы принять по условию задачи 11.9. Задачу решить при условии степенного закона упрочнения.
Определить напряженно-деформированное состояние в длинной толстостенной трубе, а также внешнее давление
 ,
если известно, что
,
если известно, что .
Рассмотреть два случая:
.
Рассмотреть два случая: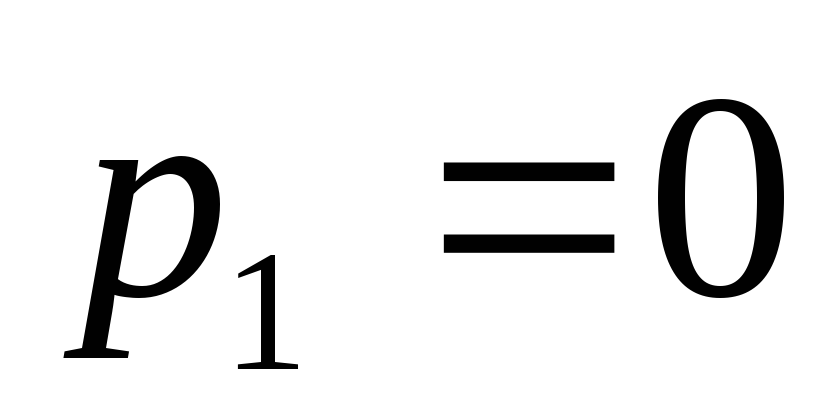 и
и .
.
Материал трубы принять по условию задачи 11.9.
Найти остаточные напряжения и закрутку после упругопластического кручения прутка круглого поперечного сечения радиусом
 из идеально упругопластического
материала на угол
из идеально упругопластического
материала на угол при следующих исходных данных: предел
текучести
при следующих исходных данных: предел
текучести МПа,
МПа, рад/м, модуль сдвига
рад/м, модуль сдвига МПа,
МПа, м,
м, - номер в списке студента в группе,
- номер в списке студента в группе, - номер группы.
- номер группы.
Решение. Будем
считать, что при кручении моментом
![]() плоские поперечные сечения прутка
остаются плоскими и за пределом упругости
материала. При этом смежные поперечные
сечения, отстоящие друг от друга на
расстоянии
плоские поперечные сечения прутка
остаются плоскими и за пределом упругости
материала. При этом смежные поперечные
сечения, отстоящие друг от друга на
расстоянии![]() ,
поворачиваются относительно друг
друга на относительный угол
,
поворачиваются относительно друг
друга на относительный угол
![]() ,
,
где
![]() – угол кручения.
– угол кручения.
Согласно теореме о разгрузке А.А. Ильюшина (рис. 14):
![]() ,
,
где
![]() – относительный остаточный угол
кручения;
– относительный остаточный угол
кручения;
![]() –относительный
угол упругой раскрутки.
–относительный
угол упругой раскрутки.

Рис. 14
Величина угловой
деформации
![]() равна углу, заключенному между образующей
круглого прутка и разверткой винтовой
линии:
равна углу, заключенному между образующей
круглого прутка и разверткой винтовой
линии:
![]() ,
,
где
![]() – текущий радиус.
– текущий радиус.
Напряженное состояние является плоским и осесимметричным, а матрицы тензоров напряжений и деформаций имеют вид
 ,
,
 .
.
При кручении моментом цилиндрического прутка в поперечных сечениях возникают только касательные напряжения
![]() .
.
В случае упругого
кручения касательные напряжения
максимальны на периферии при
![]()
![]() и по линейному закону уменьшаются,
обращаясь в нуль в центре сечения
(рис. 15):
и по линейному закону уменьшаются,
обращаясь в нуль в центре сечения
(рис. 15):

Рис. 15
Действуя на
кольцевую площадку
![]() ,
они создают элементарный момент
относительно оси, равный
,
они создают элементарный момент
относительно оси, равный![]() .
Тогда крутящий момент в упругой области
равен
.
Тогда крутящий момент в упругой области
равен
![]() ,
,
где
![]() – полярный момент инерции для круглого
поперечного сечения:
– полярный момент инерции для круглого
поперечного сечения:
![]() .
.
При увеличении
момента кручения касательное напряжение
![]() достигает по условию пластичности
Треска-Сен-Венана предельного значения
достигает по условию пластичности
Треска-Сен-Венана предельного значения
![]() ,
,
и в поверхностном
слое прутка возникает пластическая
деформация (рис. 16). При дальнейшем
увеличении
![]() пластическая деформация распространяется
вглубь. Величину радиуса
пластическая деформация распространяется
вглубь. Величину радиуса![]() ,
определяющего границу между упругой
и пластической зонами, легко найти
по формуле
,
определяющего границу между упругой
и пластической зонами, легко найти
по формуле
![]() ,
,
откуда
![]() .
.

Рис. 16
Как видно из рис. 16, периферийные слои находятся в пластическом, а центральные – в упругом состоянии. Касательные напряжения распределены в поперечном сечении следующим образом:

Крутящий момент
складывается из крутящего момента в
упругой области
![]() и крутящего момента в пластической
области
и крутящего момента в пластической
области![]() :
:
![]() .
.
После снятия
внешнего момента
![]() (разгрузки) в прутке возникнут остаточные
касательные напряжения
(разгрузки) в прутке возникнут остаточные
касательные напряжения
![]() ,
,
вызывающие
раскручивание прутка на угол
![]() (рис. 17). Момент при упругой разгрузке
равен
(рис. 17). Момент при упругой разгрузке
равен
![]() .
.
Из условия равенства
суммы моментов нагрузки и разгрузки
нулю (![]() )
находим максимальное касательное
напряжение
)
находим максимальное касательное
напряжение![]() :
:
![]() ,
,
откуда
![]() .
.
Таким образом распределение остаточных касательных напряжений имеет вид
 при
при
![]() ,
,
 при
при
![]() .
.

Рис. 17
Из рис. 17 видно, что остаточные касательные напряжения отрицательны на внешней части поперечного сечения прутка и положительны во внутренней.
Угол упругой раскрутки найдем из уравнения
![]() .
.
Окончательно имеем
![]() .
.
Остаточный угол кручения
 .
.
11.13 Для
толстостенной стальной трубы имеющей
внутренний диаметр
![]() м
и наружный диаметр
м
и наружный диаметр![]() м,
и изготовленный из пластического
материала с
м,
и изготовленный из пластического
материала с![]() МПа
требуется:
МПа
требуется:
Определить внутреннее давление
 ,
при котором в материале трубы начнется
пластическое течение по критерию
максимальных касательных напряжений.
,
при котором в материале трубы начнется
пластическое течение по критерию
максимальных касательных напряжений.Построить эпюры распределения напряжений
 и
и по толщине стенки.
по толщине стенки.
Решение.
1. По формулам из задачи 8.14 определяем давление, при котором на внутренней поверхности трубы появятся пластические деформации:
![]() ;
;

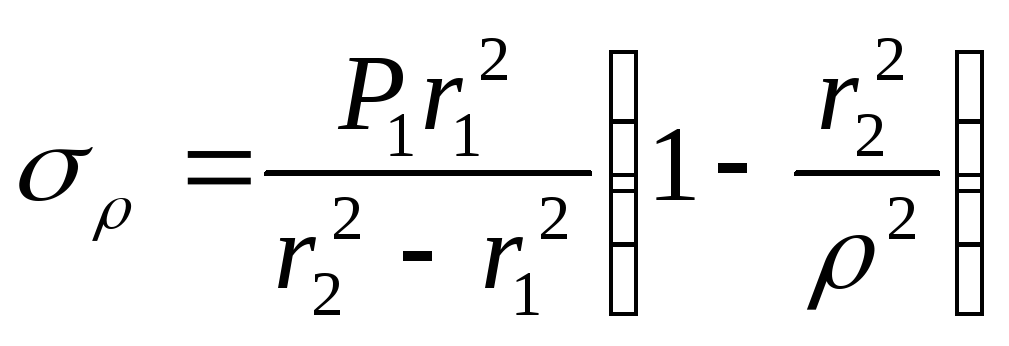 ;
;
 ,
,
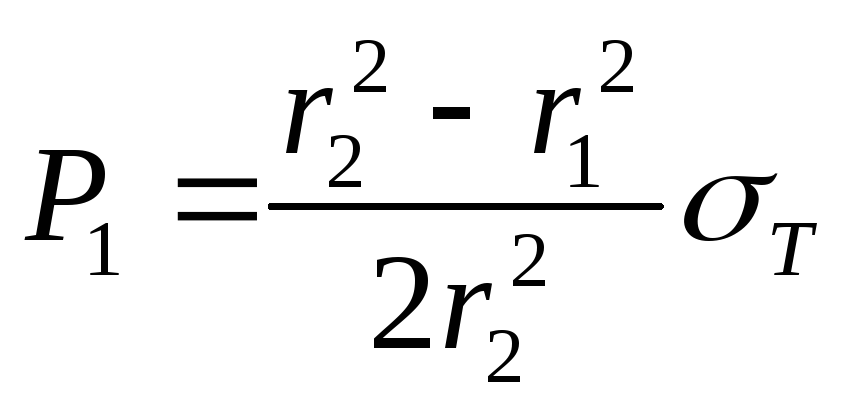 .
.
![]() .
.
2. С учетом
того, что
![]() определяем напряжения, соответствующие
началу пластичского течения:
определяем напряжения, соответствующие
началу пластичского течения:
 ,
,
 .
.
Данные числовых расчетов сводим в табл. 11:
Таблица 11

Эпюры
напряжений
![]() и
и![]() приведены на рис. 18.
приведены на рис. 18.
![]()

Рис.18
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Безухов, Н.И. Примеры и задачи по теории упругости, пластичности и ползучести. Н.И. Безухов. - М.: Высш. шк., 1965. - 320 с.
Томсен Э. Механика пластических деформаций при обработке металлов/ Э. Томсен, Ч. Янг, Ш. Кобаяши. - М.: Машиностроение, 1969. - 504 с.
Смирнов, В.С. Сборник задач по обработке металлов давлением/ В.С. Смирнов - М.: Металлургия, 1973. - 191 с.
Яковлев, С.П. Сборник задач с решениями по курсу "Теория обработки металлов давлением"/ С.П. Яковлев, И.А. Смаригдов, В.Д. Кухарь, П.Л. Макарова. Тульский политехн. ин-т, 1978. - 48 с.
Мейз, Д. Теория и задачи механики сплошных сред/ Д. Мейз. - М.: Мир, 1974.318 с.
Илюкович, Б.М. Введение в теорию пластичности/ Б.М. Илюкович. - Киев: Высш. шк. 1983. - 160 с.
Гунн, Г.Я. Теоретические основы обработки металлов давлением/ Г.Я. Гунн. - М.: Металлургия, 1980. - 456 с.
Сторожев, М.В. Теория обработки металлов давлением/ Е.А. Попов. - М.: Машиностроение, 1971. - 424 с.
