1.3.2.Метод Гаусса

Метод Гаусса заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе уравнений с тремя неизвестными:

Допустим, что (если, то изменим порядок уравнений, выбрав первым такое уравнение, в котором коэффициент приx не равен нулю.)

1 шаг: делим уравнение на , умножаем полученное уравнение наи вычитаем из ; затем умножаем на и вычитаем из (). В результате 1 шага приходим к системе:

Причем получается изпо следующим формулам:

2 шаг: поступаем с уравнениями , точно так же, как с уравнениями , , () и т.д. В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов.

ПРИМЕР 2. Решить систему уравнений

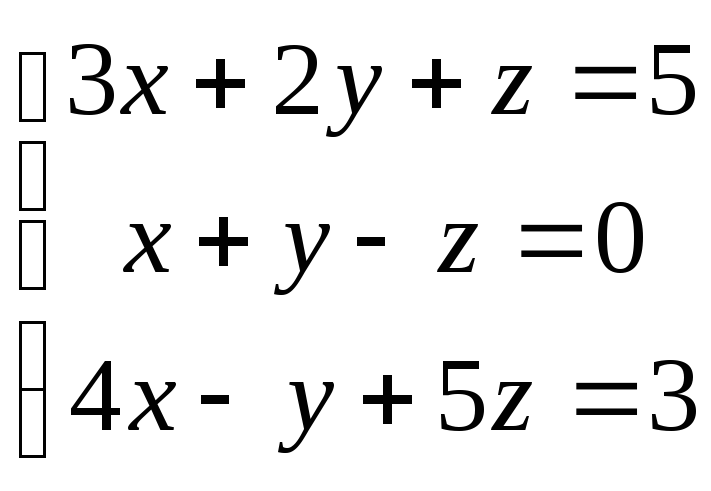
Преобразуем матрицу в эквивалентную, поменяв местами 1, 2-ю строки

~

Первые три столбца это коэффициенты при неизвестных, четвертый столбец - свободные члены данной системы, пятый - контрольный столбец, каждый элемент которого есть сумма четырех элементов данной строки.

Вычитаем из 2,3-ей строк 1-ю строку, умноженную соответственно на 3 и на 4, а затем в полученной матрице последнюю строку разделим на -11.

~

Система уравнений приняла треугольный вид:

Она имеет единственное решение. Из последнего уравнения имеем z=2; подставляя это значение во второе уравнение, получаем y=3 и, наконец, из первого уравнения находим x=-1.

1.3.3. Матричный метод

При использовании матричного метода для решения системы уравнений пользуются обратной матрицей. Этим методом можно воспользоваться только в том случае, если система имеет единственное решение.

ПРИМЕР 3. Решить систему уравнений

Перепишем систему в виде AX=B, где

Решение матричного уравнения имеет вид Найдем

Вычислим алгебраические дополнения элементов этого определителя:

Таким образом, откуда

Следовательно,

x=2, y=3, z=-2.

2. Векторная алгебра

2.1. Векторы. Действия над векторами

Геометрически вектором называется направленный отрезок. Аналитически вектор можно представить в виде упорядоченной n – 12и чисел, называемых его координатами. Обозначения вектора:, где А – начало вектора, В – его конец. Пусть в пространстве R3 известны координаты начала и конца вектора:и, тогда координаты вектора находятся по формуле

.

Пусть известны координаты двух векторов и, тогда их скалярным произведением называется число, вычисляемое по формуле:

.

Длину вектора можно вычислить по формуле:.

Косинус угла φ между векторами иможно найти следующим образом.

ПРИМЕР 1. Даны координаты трех точек А(1;-2;3), В(2;0;1), С(-1;3;1). Найти:

а). длину отрезка АВ;

б). величину угла

Решение: Найдем координаты векторов и:

.

Длину отрезка АВ найдем как длину вектора :

.

Для того, чтобы найти угол между отрезками АВ и АС, найдем сначала длину вектора :. Вычислим значение косинуса угла φ – угла между векторамии:

.

Таким образом, .

2.2. Линейная независимость векторов

Система векторов называется линейно независимой, если векторное равенствовыполняется только при условии

Например, пусть известны координаты трех векторов . Тогда система трех векторов будет линейно независимой, если значение определителя, составленного из их координат, отлично от нуля, т.е.

Если три вектора линейно независимы, то они могут быть базисом в пространстве R3. Это означает, что любой другой векторможет быть представлен в виде линейной комбинации векторов базиса:

Тогда значения , найденные из этого векторного равенства, будут являться координатами векторав базисе, а само векторное равенство называется разложением векторапо базису.

ПРИМЕР 2: Даны координаты трех векторов

.

а) доказать, что система этих трех векторов линейно независима;

б) найти разложение вектора по базису.

Решение:

а) Составим определитель из координат векторов и найдем его значение:

Т.к. значение определителя отлично от нуля, то система векторов линейно независима.

б). Составим векторное равенство: . Подставим в него координаты векторов:. Составим систему линейных уравнений:

Решая эту систему любым методом (Крамера, Гаусса), получим . Таким образом, разложение векторапо базисубудет таким:.