Ю.Ю. Громов и др. Информатика (2007)

в) шестнадцатеричная система

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Например, сложим числа 15 и 6 в различных системах счисления.

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.25 в этой форме можно представить так:

1.25 100 = 0.125 101 = 0.0125 102 = ...

или так: 12.5 10–1 = 125.0 10–2 = 1250.0 10–3 = ... .

Любое число X в системе счисления с основанием s можно записать в виде X = Ms p , где M – множитель, содержащий все цифры числа (мантисса), а p – целое число, называемое порядком. Такой способ записи чисел называется представлени-

ем числа с плавающей точкой.

Если мантисса числа является правильной дробью, у которой первая цифра после точки отлична от нуля, то такое чис-

ло называется нормализованным.

Мантиссу и порядок s-ичного числа принято записывать в системе с основанием s, а само основание – в десятичной системе. Примеры нормализованного представления:

а) десятичнаясистема753.15 = 0.75315 103; –0.000034 = –0.34 10–4; б) двоичная система –101.01 = –0.10101 211 (порядок112 = 310);

0.000011 = 0.11 2–100; (порядок–1002 = –410).

Основные понятия алгебры логики. Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики

возникла в середине ХIХ в. в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Одним из основных понятий алгебры логики является логическое высказывание. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Так, например, предложение "6 – четное число" следует считать высказыванием, так как оно истинное. Предложение "Рим – столица Франции" тоже высказывание, так как оно ложное.

Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "студент первого курса" и "информатика – интересный предмет". Первое предложение ничего не утверждает о студенте, а второе использует слишком неопределенное понятие "интересный предмет". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.

Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание "площадь поверхности Индийского океана равна 75 млн. кв. км" в одной ситуации можно посчитать ложным, а в другой – истинным. Ложным – так как указанное значение неточное и вообще не является постоянным. Истинным – если рассматривать его как некоторое приближение, приемлемое на практике.

Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если ..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логиче-

скими связками.

Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.

Так, например, из элементарных высказываний "Петров – студент", "Петров – шахматист" при помощи связки "и" можно получить составное высказывание "Петров – студент и шахматист", понимаемое как "Петров – студент, хорошо играющий в шахматы".

При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров – студент или шахматист", понимаемое в алгебре логики как "Петров или студент, или шахматист, или и студент и шахматист одновременно".

Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.

Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В – высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" – логическая связка, А, В – логические переменные, которыемогутприниматьтолько двазначения– "истина" или"ложь", обозначаемые, соответственно, "1" и"0".

Каждая логическая связка рассматривается как операция над логическими высказываниями (или логическими переменными) и имеет свое название и обозначение:

НЕ Операция, выражаемая связкой "не", называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание A истинно, когда A ложно, и ложно, когда A истинно. Зависимость между такими высказываниями

можно записать в виде таблицы истинности (рис. А.1). Пример: "Луна – спутник Земли" (А); "Луна – не спутник Земли" ( A ).

Рис. А.1

И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой " " (может также обозначаться знаками или &). Высказывание А В истинно тогда и только тогда, когда оба высказывания А и В истинны (рис. 1, б). Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а

высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" – лож-

ны.

ИЛИ Операция, выражаемая связкой "или", называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком (или плюсом). Высказывание А В ложно тогда и только тогда, когда оба высказывания А и В ложны (рис. 1, в). Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на

2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" – истинны.

Есть и другие логических операций, однако их можно выразить через отрицание, дизъюнкцию и конъюнкцию. Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.

Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции – дизъюнкция

("или").

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т.е.

заменить логической формулой.

Определение логической формулы следующее:

1.Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") – формулы.

2.Если А и В – формулы, то A , А В, А В – формулы.

3.Никаких других формул в алгебре логики нет.

В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул. Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Та-

ковой будет, например, формула A A , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истиннымивысказываниями.

В качестве другого примера рассмотрим формулу A A , которой соответствует, например, высказывание "Иванов са-

мый высокий студент в группе, и в группе есть студенты выше Иванова". Очевидно, что эта формула ложна, так как либо

А, либо A обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Если две формулы А и В одновременно, т.е. при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

Равносильность двух формул алгебры логики обозначается символом "=" или символом "≡" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.

Б. ЭЛЕКТРОННЫЕ СХЕМЫ ОБРАБОТКИ ЧИСЕЛ

ВДВОИЧНОМ ДОПОЛНИТЕЛЬНОМ КОДЕ

Вэтом приложении описаны электронные схемы, предназначенные для изменения знака числа на противоположный и для сложения чисел, представленных в двоичном дополнительном коде. Начнем обсуждение со схемы, представленной на рис. Б.1. Она позволяет преобразовать четырехразрядное число в двоичном дополнительном коде в битовую комбинацию, которая представляет то же число, но с противоположным знаком. Например, двоичный код числа 3 будет преобразован в двоичное представление числа –3. Данная схема выполняет данную операцию в соответствии с алгоритмом, описанным в главе 1. Это значит, что схема копирует входную битовую комбинацию на выход в направлении справа налево до тех пор, пока не встретит разряд со значением 1, а затем формирует на выходе дополнения каждого оставшегося входного бита. Поскольку на первый вход самого правого логического элемента XOR (исключающее "ИЛИ") постоянно поступает значение 0, этот элемент просто передает на выход значение на другом его входе. Однако этот выходной сигнал одновременно поступает

ина первый вход следующего логического элемента XOR. Если это выходное значение будет равно 1, то этот логический элемент XOR сформирует на выходе дополнение для его второго входного сигнала.

Рис. Б.1. Электронная схема, изменяющая знак числа в двоичном дополнительном коде на противоположный

Кроме того, этот же единичный сигнал от первого элемента XOR через логический элемент OR (логическое "ИЛИ") подается на правый вход третьего элемента XOR, чтобы оказать соответствующее влияние на работу этого логического элемента. Таким образом, первая же единица (справа), которая появится в выходной комбинации, автоматически передается влево, на входы логических элементов старших разрядов, а это приводит к тому, что для всех оставшихся битов числа на выходе будут сформированы их дополнения.

Далее рассмотрим процесс сложения двух чисел, представленных в двоичном дополнительном коде. Например, рассмотрим решение следующей задачи:

0110 + 1001

Сложение выполняется суммированием отдельных разрядов "по столбцам" в направлении справа налево с использованием одного и того же алгоритма для каждого столбца. Таким образом, если построить электронную схему для сложения значений в одном столбце, то схему для сложения чисел из нескольких столбцов (двоичных разрядов) можно создать, просто копируя в необходимом количестве схему, выполняющую суммирование для одного столбца.

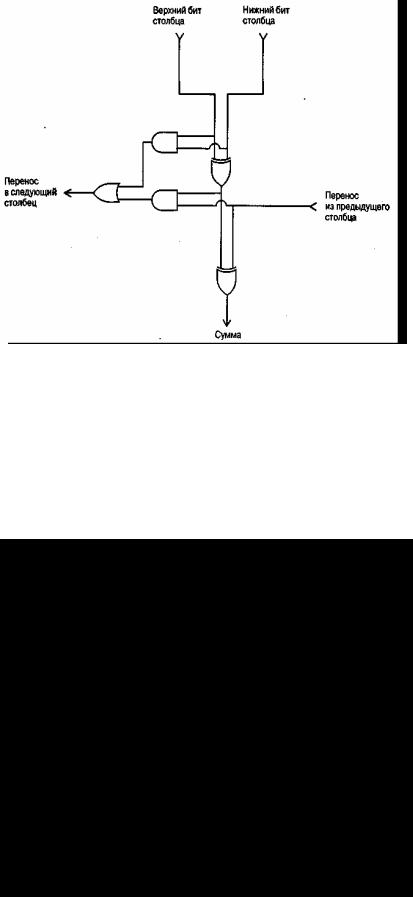
Рис. Б.2. Электронная схема для сложения значений в отдельном столбце

Алгоритм сложения значений в отдельном столбце для задачи сложения чисел из нескольких столбцов состоит в следующем. Требуется сложить два значения в текущем столбце, добавить эту сумму к биту, перенесенному из предыдущего столбца, записать младший значащий бит этой суммы в бит результата и перенести значение избыточного бита в следующий столбец. Электронная схема, реализующая этот алгоритм, представлена на рис. Б.2. В этой схеме верхний логический элемент XOR определяет сумму входных битов, нижний элемент XOR складывает полученную сумму со значением, перенесенным из предыдущего столбца. Два логических элемента AND (логическое "И") вместе с логическим элементом OR передают бит переноса налево. Поэтому если в данном столбце оба суммируемых бита равны 1 или сумма входных битов и бит переноса одновременно равны 1, то в соседний разряд будет перенесено значение 1.

На рис. Б.3 показано, как несколько копий данной схемы суммирования значений в одном столбце можно использовать для построения электронной схемы, вычисляющей сумму двух чисел, представленных в четырехразрядном двоичном дополнительном коде. На этой схеме

Рис. Б.3. Электронная схема сложения двух четырехразрядных чисел в двоичном дополнительном коде, построенная из четырех копий схемы, представленной на рис. Б.2

каждый прямоугольник представляет собой копию рассмотренной выше электронной схемы суммирования одного разряда. Обратите внимание, что значение бита переноса, поступающее на вход крайнего справа прямоугольника, всегда равно 0, поскольку для этого разряда никакого переноса из предыдущего столбца не существует. Кроме того, бит переноса из крайнего левого прямоугольника просто игнорируется.

Схема на рис. Б.3 называется сумматором со сквозным переносом, поскольку перенос должен проходить сквозь всю схему, от крайнего правого до крайнего левого столбца. Несмотря на простоту реализации, такие схемы медленнее выполняют свои функции по сравнению с более совершенными схемами, такими как сумматор с ускоренным переносом, минимизирующий переносы от столбца к столбцу. Поэтому схема, изображенная на рис. Б.3, хотя и подходит для наших целей, тем не менее, в современных вычислительных машинах не используется.

В. ПРИМЕР ТИПИЧНОГО МАШИННОГО ЯЗЫКА

Архитектура машины. Рассматриваемая гипотетическая машина имеет 16 регистров общего назначения, пронумерованных от 0 до F (в шестнадцатеричной системе счисления). Длина каждого регистра равна одному байту (восьми битам). Для идентификации регистров в машинных командах каждому регистру присвоен уникальный четырехразрядный двоичный код, который представляет собой номер этого регистра. Таким образом, регистр 0 идентифицируется как 0000 (шестнадцатеричный 0), а регистр 4 – как 0100 (шестнадцатеричное 4).

Поскольку память рассматриваемой машины состоит из 256 ячеек, каждая ячейка будет иметь уникальный адрес, представляющий собой целое число в диапазоне от 0 до 255. Следовательно, адрес любой ячейки памяти может быть представлен восьмибитовыми числами от 00000000 до 11111111 (вшестнадцатеричном представленииот00 доFF).

Предполагается, что числа с плавающей запятой хранятся в следующем формате:

Машинный язык. Длина каждой машинной команды равна двум байтам. Первые четыре бита содержат код операции, последние 12 битов образуют поле операндов. В приведенной ниже таблице перечислены и кратко описаны команды, показанные в шестнадцатеричном представлении. Буквы R, S и Т используются для указания в поле операндов позиции шестнадцатеричных цифр, являющихся идентификаторами регистров, которые меняются в зависимости от конкретной команды. Буквы X и Y используются для указания в поле операндов позиций тех шестнадцатеричных цифр, которые не являются идентификаторами регистров.

Таблица

Г. ПРИМЕРЫ ПРОГРАММ

В этом приложении приведены примеры программ на языках Ada, С, C++, FORTRAN, Java и Pascal. Каждая из программ получает на вход список имен, поступающий с клавиатуры, сортирует его с помощью алгоритма сортировки вставками и выводит отсортированный список на экран дисплея.

Язык Ada. Язык программирования Ada, названный в честь Августы Ады Байрон (Augusta Ada Byron) (1815 – 1851), помощницы Чарльза Бэббиджа (Charles Babbege) и дочери поэта лорда Байрона, был создан по инициативе министерства обороны США. Военные хотели получить единый язык общего назначения, который можно было бы использовать во всех разработках программного обеспечения, проводимых в этом министерстве. Основной упор при разработке языка Ada был сделан на средствах программирования компьютерных систем реального времени, которые являются частью более крупных систем, таких, как системы управления полетами ракет, системы контроля состояния окружающей среды, системы управления в автомобилях и небольшие домашние системы управления. В результате в язык Ada были включены возможности про-

граммирования параллельных процессов, а также удобные средства для обработки особых случаев (называемых исключительными ситуациями), которые могут возникать при работе систем. Самая современная версия языка Ada, известная как Ada 95, охватывает также объектно-ориентированную парадигму программирования.

Пример программы на языке Ada приведен на рис. Г.1.

Язык С был разработан в начале 1970-х гг. Деннисом Ритчи (Dennis Ritchie), работавшим в то время в компании Bell Laboratories. Хотя первоначально язык С создавался для разработки операционных систем и компиляторов, он быстро получил популярность в среде программистов и приобрел дополнительные преимущества благодаря его стандартизации, выполненной Американским институтом национальных стандартов (ANSI – American National Standards Institute).

Язык С сначала рассматривался просто как некоторый шаг вперед по сравнению с машинным языком. По этой причине его синтаксис более краток и выразителен, чем синтаксис других языков высокого уровня, использующих полные слова английского языка для выражения тех языковых конструкций, которые в языке С представляются с помощью специальных символов. Эта лаконичность является одной из причин чрезвычайной популярности языка С, поскольку позволяет программистам эффективно выражать сложные алгоритмы. (Часто краткое представление алгоритма более доступно пониманию, чем его пространное описание.)

Пример программы на языке С приведен на рис. Г.2.

--Программа обработки списка with TEXT_IO;

usе ТЕХТ_IO; procedure MAIN is

subtype NAME.TYPE is STRING (1..8); LIST_LENGTH: constant:=10;

NAMES: array (1..LIST_LENGTH) of NAME_TYPE; PIVOT: NAME_TYPE; HOLE: INTEGER;

begin

--Прежде всего получаем список имен с клавиатуры for К in 1 .. LIST_LENGTH loop

GET(NAMES(К)); end loop;

--Сортируем список(переменнаяHOLE содержит номер пропуска в --списке с момента удаления элемента из списка и до момента --его повторной вставки)

for N in 2 .. LIST_LENGTH loop PIVOT := NAMES(N);

HOLE := N;

for M in reverse 1 .. N-l loop if NAMES(M) > PIVOT

then NAMES(M+l) := NAMES(M); else exit;

end if; HOLE := M;

end loop;

NAMES(HOLE) := PIVOT; end loop;

--Теперь печатаем отсортированный список for К in 1 .. LI STRENGTH loop

NEW_LINE; PUT(NAMES(K));

end loop; end MAIN;

Рис. Г.1. Пример программы на языке Ada

/* Программа обработки списка */ #include <stdio.h>

#include <string.h> main()

{

char names[10][9], pivot[9]; int i, j;

/* Ввод имен с клавиатуры */ for(i = 0; i < 10; ++i)

scanf("%s", names[i]);

/* Сортировка списка имен */ for(i = 1; i < 10; ++i)

{ strcpy(pivot,names[i]); j = i - 1;

while((j>=0) && (strcmp(pivot, names[j]) < 0) { strcpy(names[j+1], names[j]);

--j;

}

strcpy(names[j+1],pivot);

}

/* Печать отсортированного списка */ for( i = 0; i < 10; ++i)

printf("%s\n", names[i]);

}

Рис. Г.2. Пример программы на языке С

Язык C++ был разработан Бьярни Страуструпом (Bjarne Strausstrup) из компании Bell Laboratories как усовершенствованная версия языка С. Цель создания языка C++ – достижение совместимости языка С с объектно-ориентированной парадигмой программирования.

Реализация алгоритма сортировки вставками на языке C++ представлена на рис. Г.3. Последние четыре оператора этой программы требуют, чтобы объект namelist был создан как объект, имеющий "тип" (класс) list, после чего новый объект должен выполнить операции getnames, sortnames и printnames. Предыдущий фрагмент программы определяет свойства, которыми должны обладать любые объекты "типа" (класса) list. В частности, любой такой объект должен содержать массив символов под названием names и три процедуры – getnames, sortnames и printnames. Обратите внимание, что определения этих

//Программа обработки списка

#include <iostreain.h> #include <string.h> const int ListLength = 10;

//Все объекты класса list содержат список имен и три открытых

//метода, которые называются getnames, sortlist и printnames. class list

{ private:

char names[ListLength][9]; public:

void getnames()

{int i;

for(i = 0; i< ListLength; *+i) cin » names[i];

}

void sortlist() { int i,j;

char pivot[9];

for(i = 1; i < ListLength; ++i) { strcpy(pivot, names[i]);

j = i - 1;

while((j >= 0) && (stremp(pivot, names[j]) < 0)) { strcpy(names[j+1], names[j]);

--j;

}

strcpy(names[j+1],pivot);

}