4.3.8. Интегрирование тригонометрических функций

Интегралы от тригонометрических функций сводится к интегралам от рациональных функций с помощью специальных подстановок.

1. Универсальная тригонометрическая подстановка

позволяет любой интеграл вида , гдеR – рациональная функция, привести к интегралу от рациональной функции.

Найдем ,,,.

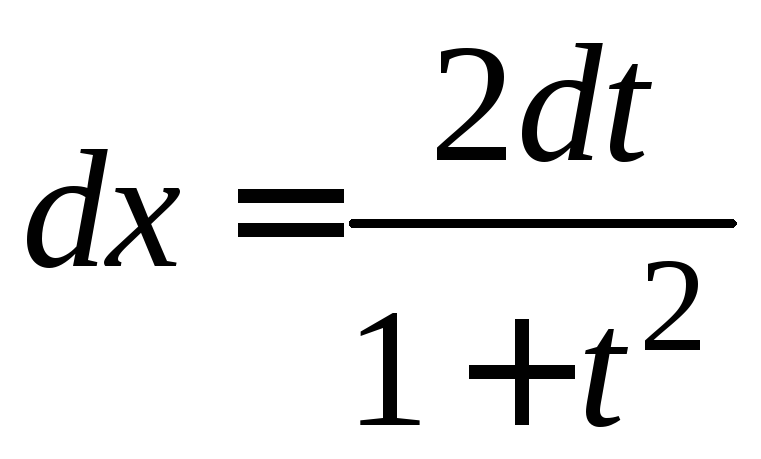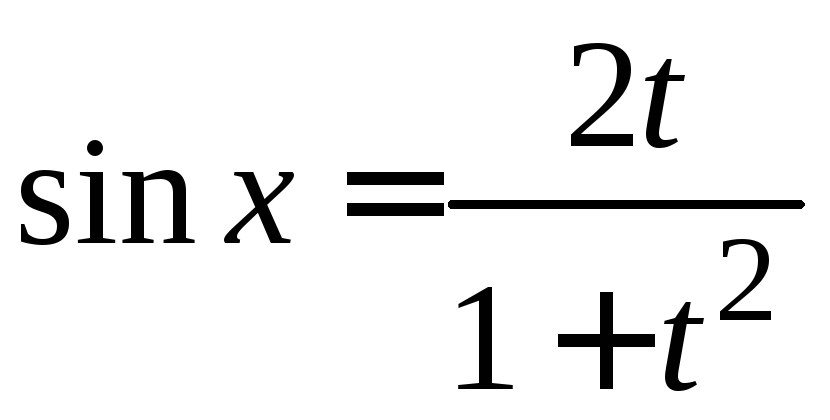Пример 4.32. .

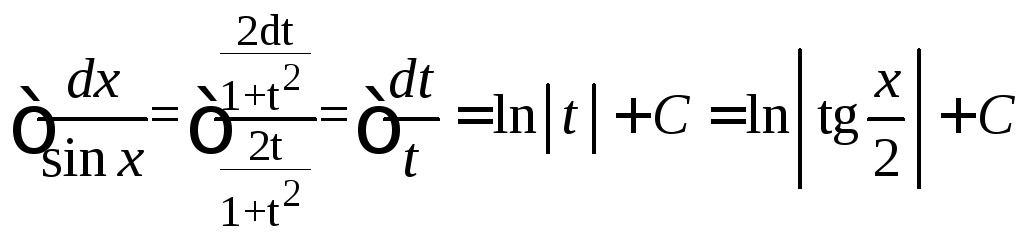Для интегралов от тригонометрических функций частных видов более удобными могут быть другие подстановки.

2. Если интеграл имеет вид , то применяется подстановка. Тогдаи интеграл примет вид.

3. Если интеграл имеет вид , то применяется подстановка. Тогдаи интеграл примет вид.

Пример 4.33.

.

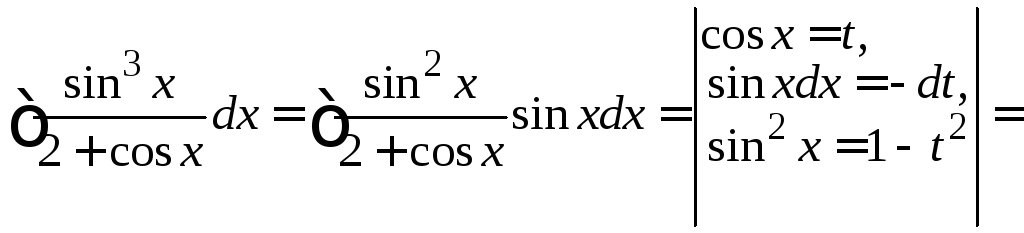
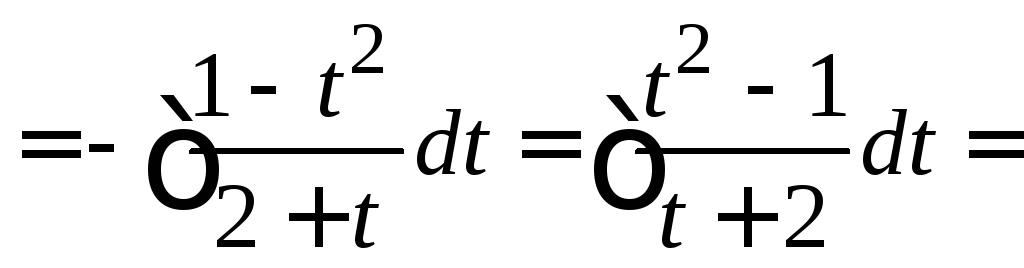
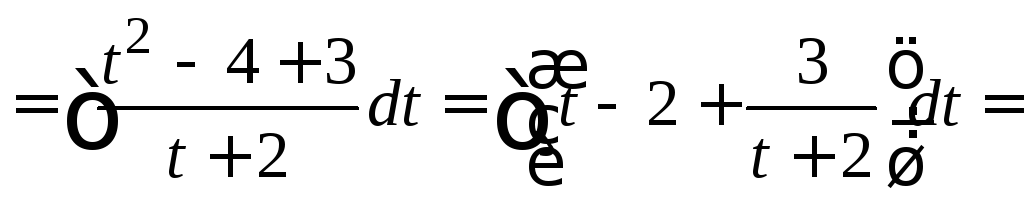
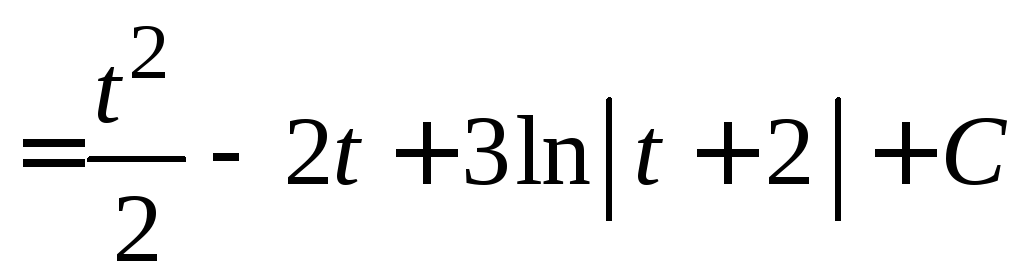
4. Если интеграл , то целесообразно применить подстановку. Тогда,. В результате подстановки интеграл примет вид.

Пример 4.34. =.

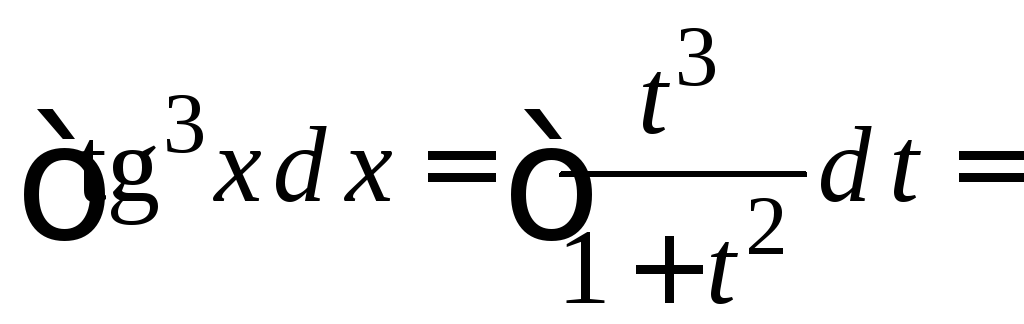
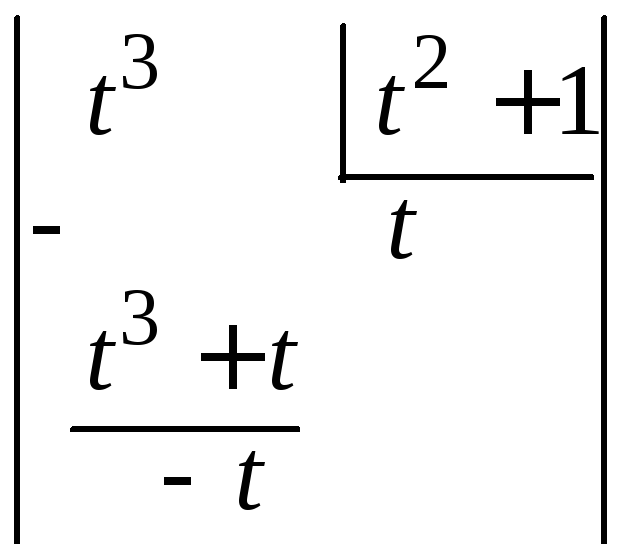5. Если , где, то лучше применить подстановку. Тогда,

, ,.

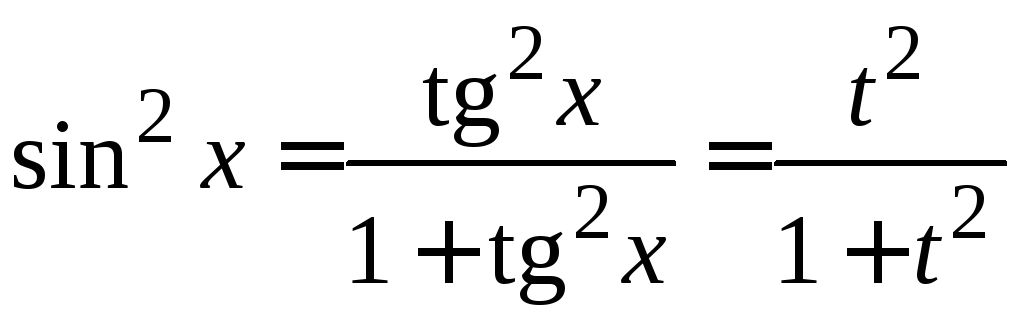Пример 4.35. .

6. Если интеграл имеет вид , где, то применяют подстановки следующих видов:

если степень синуса n нечетная, то ;

если степень косинуса m нечетная, то ;

если m и n четные, то применяют формулы понижения степени

.

Пример 4.36. .

7. Если интеграл имеет вид ,,, то применяют формулы преобразования произведения тригонометрических функций в сумму:

,

,

.

Пример 4.37. .

4.3.9. Интегрирование иррациональных функций с помощью тригонометрических подстановок

Интегралы вида с помощью выделения полного квадрата в квадратном трехчлене и элементарной подстановки могут быть приведены к одному из следующих видов:

1) , 2),

3) .

Для интегралов вида используется подстановка

или .

Для интегралов вида используется подстановка

или .

Для интегралов вида используется подстановка

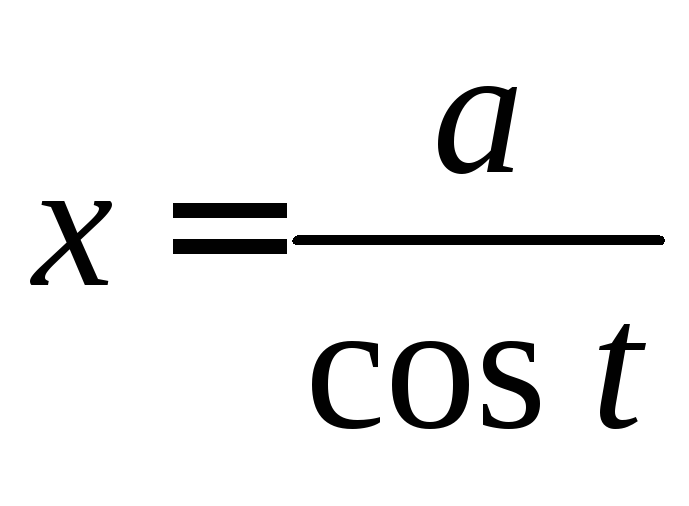или .

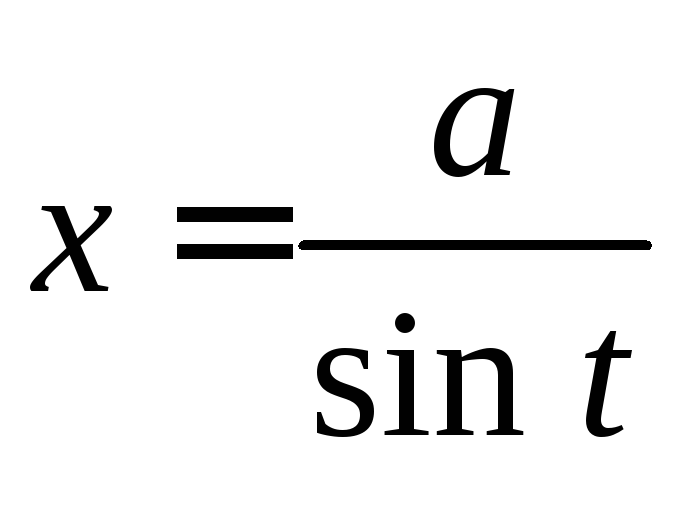Пример 4.38. =

.

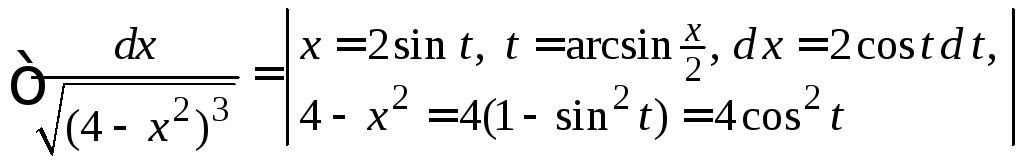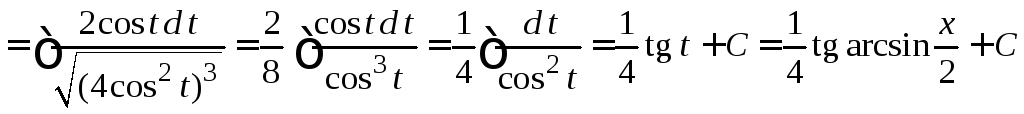Пример 4.39.

=

.

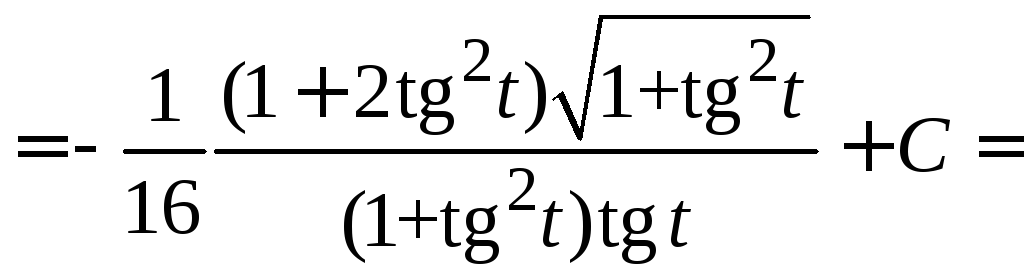
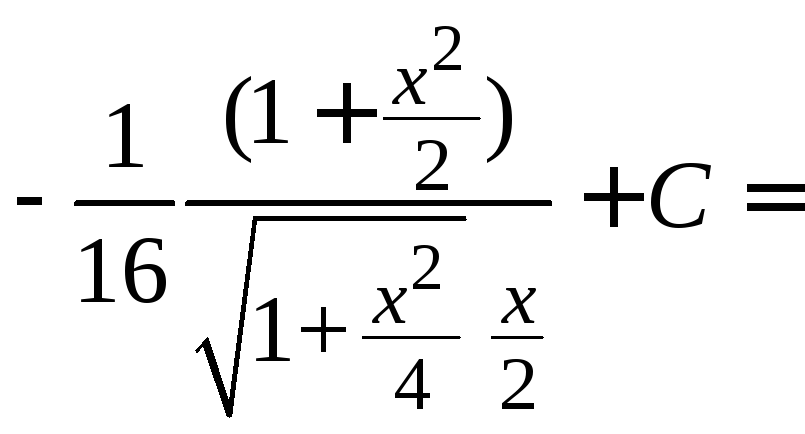
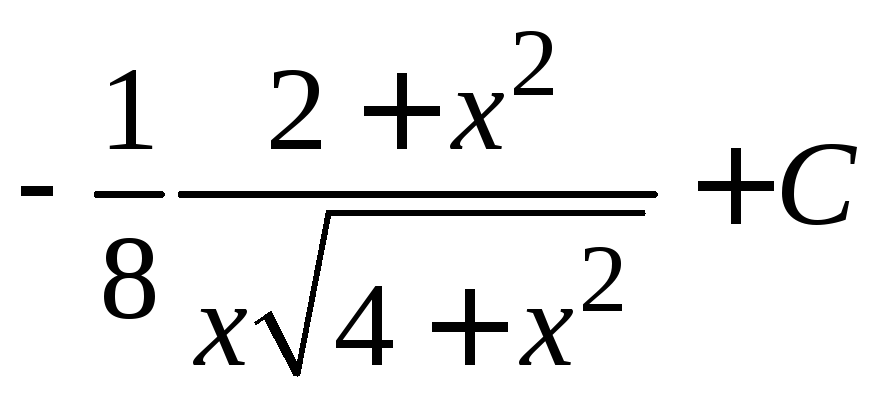Пример 4.40.

.

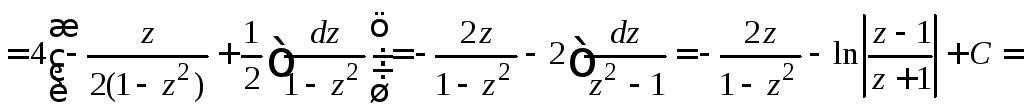
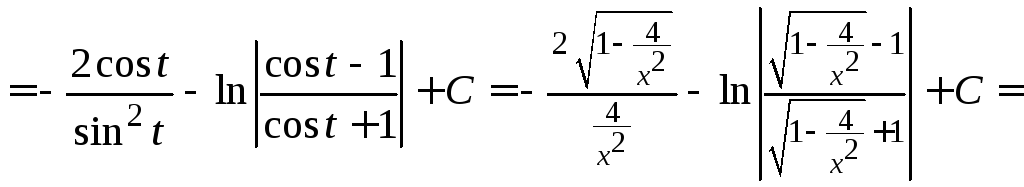
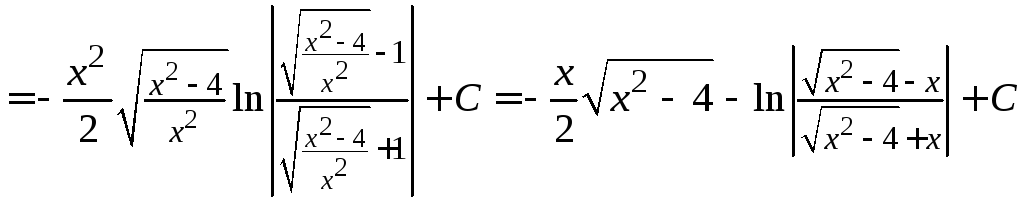4.4. Об интегрировании в конечном виде

Как было показано выше, любая функция непрерывная на отрезкеимеет первообразную функцию. Однако не всякая функция первообразная выражается в конечном виде через элементарные функции. Такими первообразными являются, например, первообразные выраженные интегралами.

Для некоторых из таких функций составляются таблицы и эти функции используются при решении прикладных задач. Например, функция

,

которая обращается в нуль при х = 0 называется функцией Лапласа используется в теории вероятности и математической статистике.

29