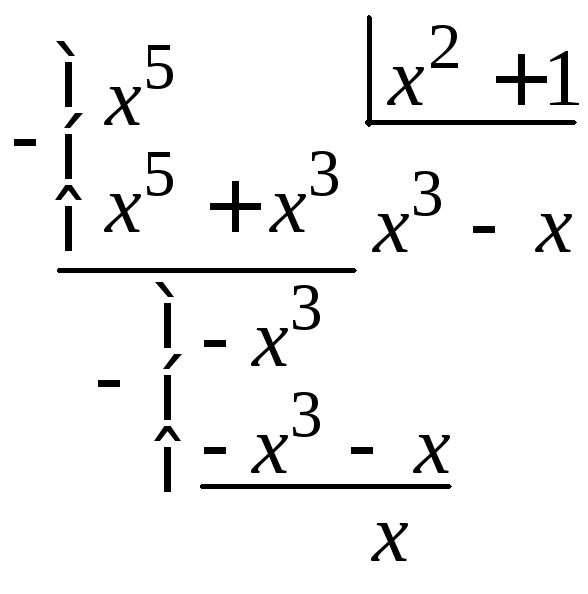4.3.3. Интегрирование функций, содержащих квадратный трехчлен

Рассмотрим интегралы четырех типов.

I. Интеграл вида . Необходимо в знаменателе выделить полный квадрат. Затем после замены переменной интеграл примет вид табличного интеграла.

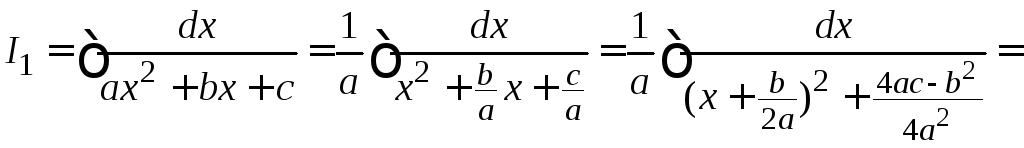
Пример 4.17. .

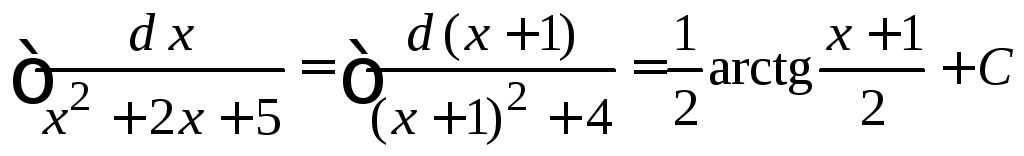Пример 4.18.

.

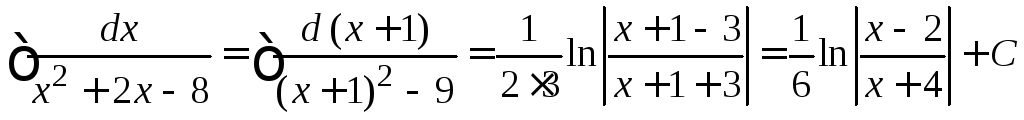II. Интеграл вида . Данный интеграл сводится к интегралу первого типа. Для этого в числителе подынтегральной функции нужно сформировать производную квадратного трехчлена, стоящего в знаменателе. Найдем производную. Затем интеграл разбить на сумму двух интегралов, первый из которых равен логарифму квадратного трехчлена, а второй является интегралом первого типа.

.

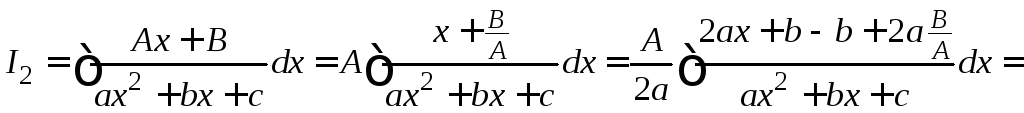
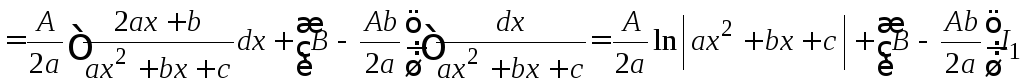Пример 4.19.

.

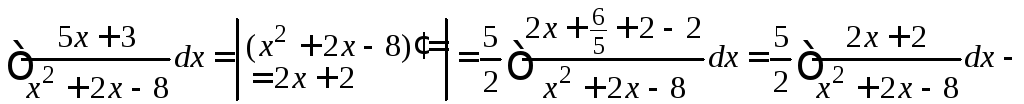
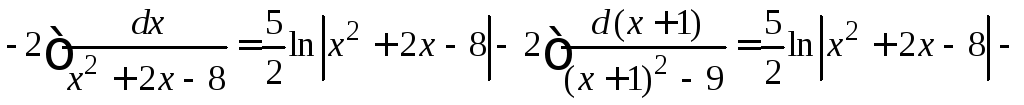
III. 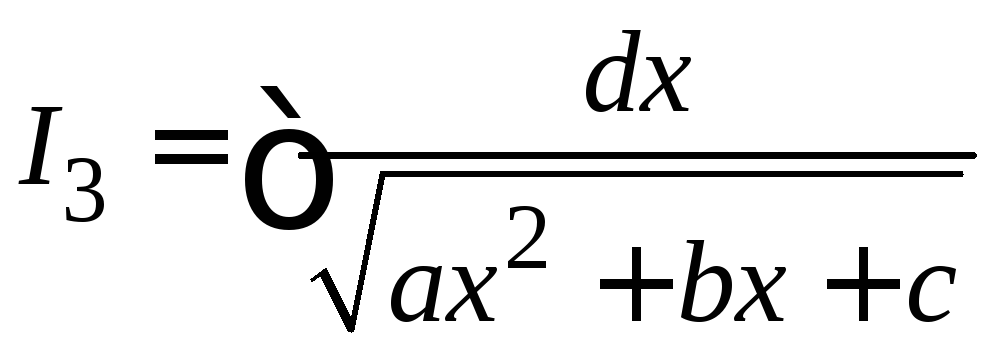. Также как в интеграле первого типа, в квадратном трехчлене выделим полный квадрат, а затем сделаем замену переменной.

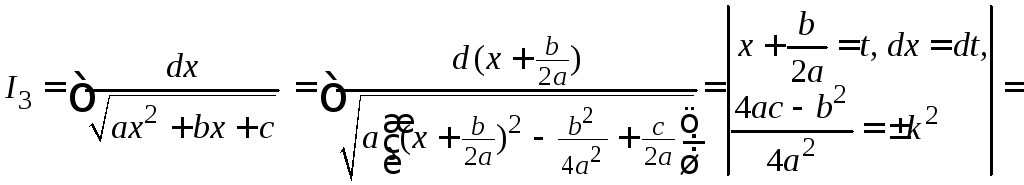
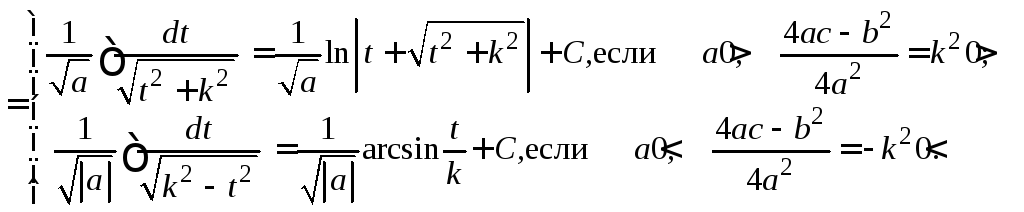
IV. . Данный интеграл сводится к интегралу третьего типа. Для этого в числителе подынтегральной функции нужно сформировать производную квадратного трехчлена, стоящего под корнем в знаменателе. Интеграл разбить на сумму двух интегралов, первый из которых равен квадратному корню, а второй является интегралом третьего типа.

+.

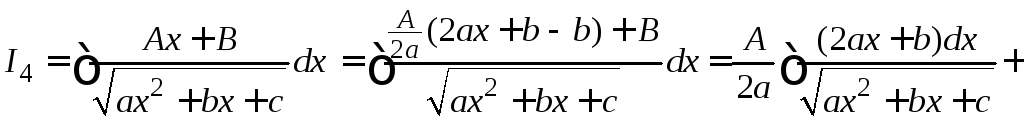
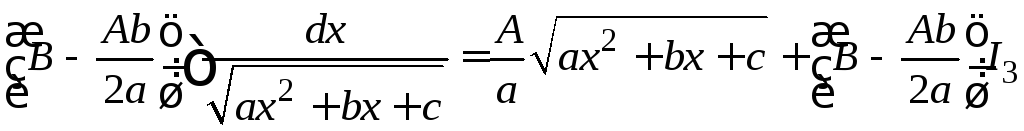Пример 4.19.

.

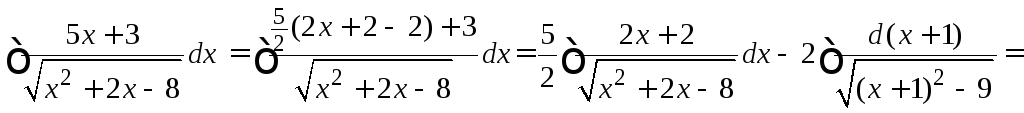
Пример 4.20.

.

4.3.4. Метод интегрирования по частям неопределенных интегралов

Пусть идифференцируемые функции. Известно, что

.

Найдем неопределенные интегралы от функций, стоящих в левой и правой частях этого равенства, получим

.

Используем третье и пятое свойства интегралов, получим

.

Отсюда получается формула, которая называется формулой интегрирования по частям

.

Для лучшего запоминания запишем эту формулу в виде

.

Следовательно, если подынтегральное выражение можно разбить на итак, что можно найтии, то исходный интеграл можно свести к нахождению другого интеграла, который возможно находится проще.

Имеются некоторые общие соображения о применении этого метода.

Так, если подынтегральная функция содержит произведение многочлена

и одной из следующих функций:

,

то такие функции нужно принять за , а многочлен включить в().

Пример 4.21.

.

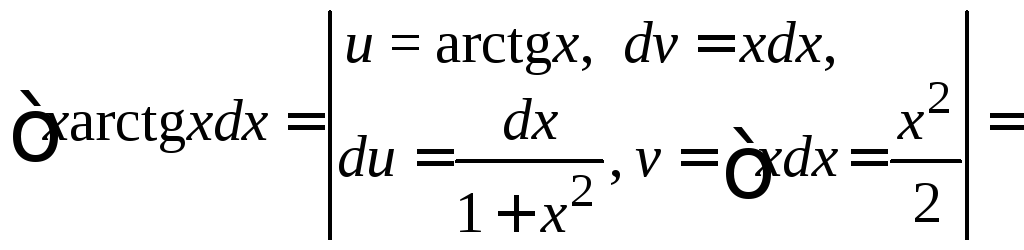
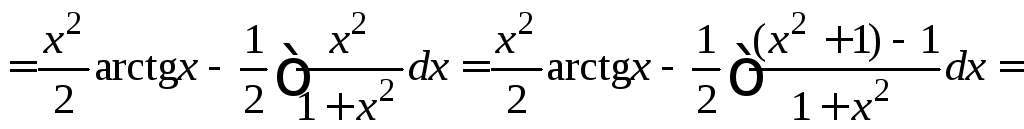
Если же под интегралом имеется произведение многочлена и одной из функций:

,

то за нужно принять многочлен, а завсе остальное подынтегральное выражение. При этом если степень многочлена больше единицы, то интегрирование по частям необходимо повторить столько раз, какова степень многочлена.

Пример 4.22.

.

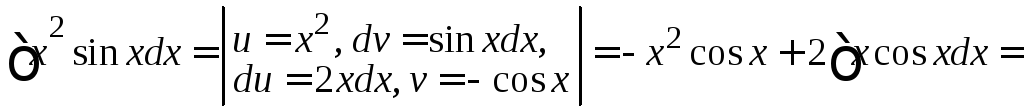
Если под интегралом имеется произведение функции илина тригонометрическую функциюили, то в результате двукратного интегрирования по частям получается уравнение относительно исходного интеграла (интеграл возвращается к первоначальному виду). Такие интегралы называются «возвратными».

Пример 4.23.

.

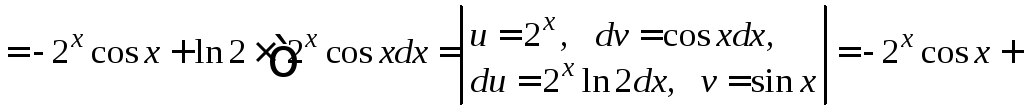
Получили уравнение относительно исходного интеграла

.

Отсюда .

Пример 4.24.

.

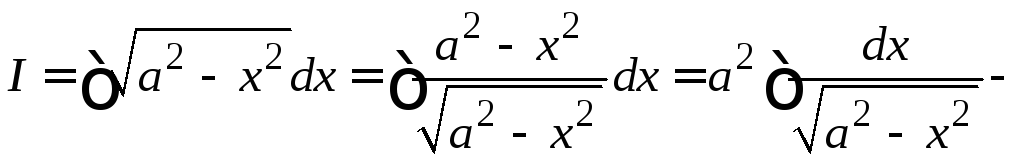
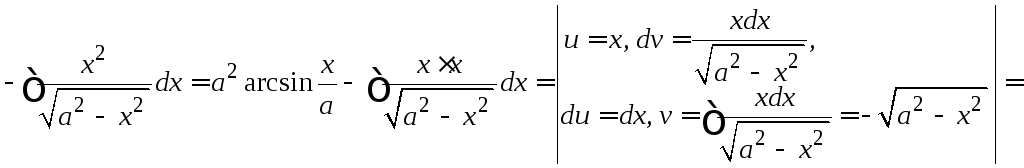
Отсюда получаем



.

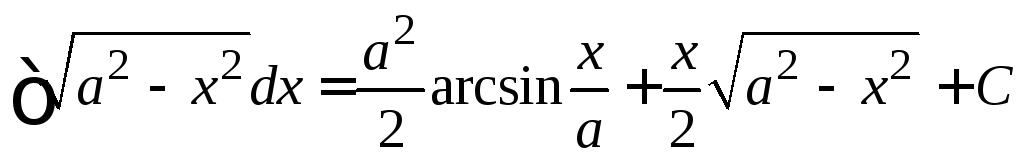4.3.5. Интегрирование дробно-рациональных функций

Пусть требуется найти неопределенный интеграл вида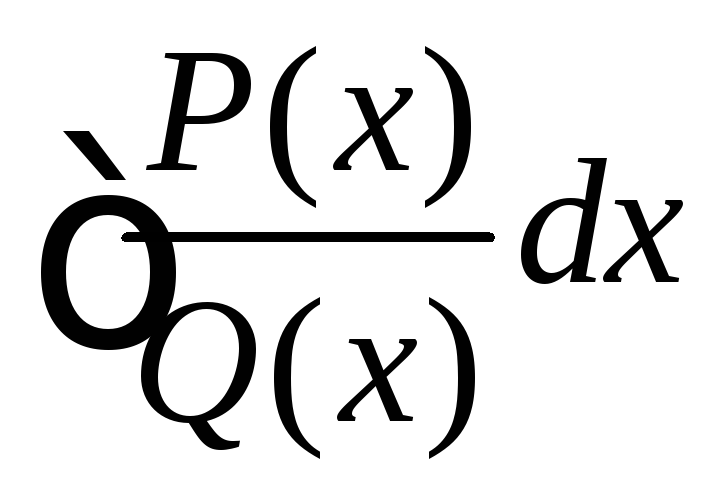, где

и .

Если степень n многочлена, стоящего в числителе, больше степени m, многочлена, стоящего в знаменателе, т. е. , то необходимо в первую очередь выделить целую часть. Для этого можно использовать деление уголочком.

Например, пусть имеется неправильная дробь . Делим и получаем

Если дробь правильная, т. е., то многочлен, стоящий в знаменателе, нужно разложить на множители видаи,

где m и n степени кратности множителей. Здесь предполагается, что квадратный трехчлен не имеет вещественных корней. При разложении дробина сумму простых дробей каждому множителю будет соответствовать столько слагаемых, какова его степень. Например,

.

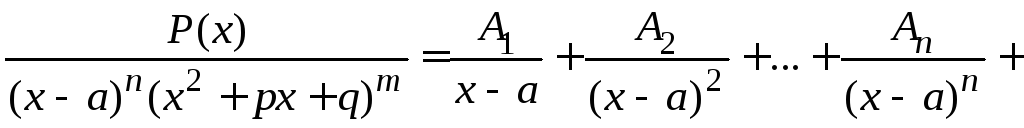
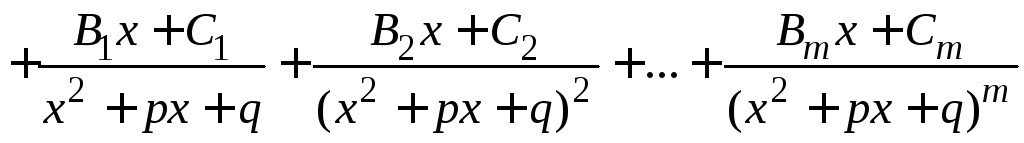Для того чтобы найти постоянные коэффициенты

в данном разложении, необходимо сумму дробей привести к общему знаменателю и приравнять многочлены, стоящие в числителях левой и правой частей. Для нахождения коэффициентов составляется система линейных уравнений. При этом возможно использовать два способа. В одном из них приравниваются коэффициенты при одинаковых степенях переменной х в многочленах левой и правой частей. В другом способе приравниваются значения многочленов при каких-либо специально выбранных значениях х. Возможно также совместное применение этих способов.

Пример 4.25. Найти интеграл .

Разложим подынтегральную функцию на простые дроби

.

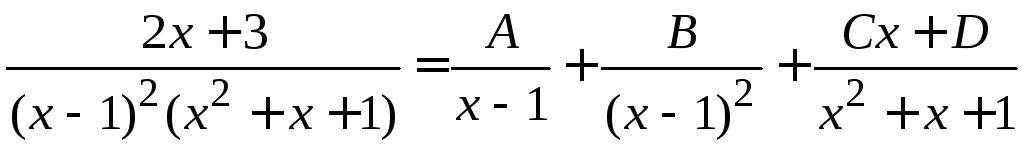Приведем сумму простых дробей к общему знаменателю

Приравниваем числители дробей

.

.

Приравниваем коэффициенты при одинаковых степенях х многочленов левой и правой частей, получаем систему и решаем ее.

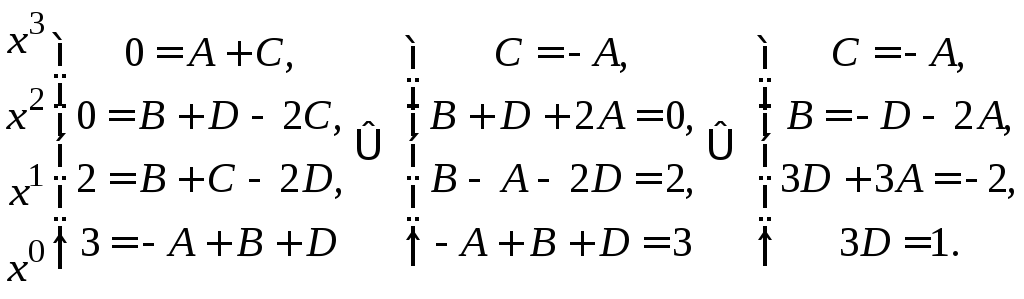
Получаем решение системы

, .

Находим интеграл

.

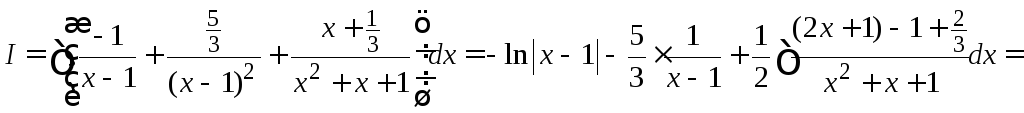
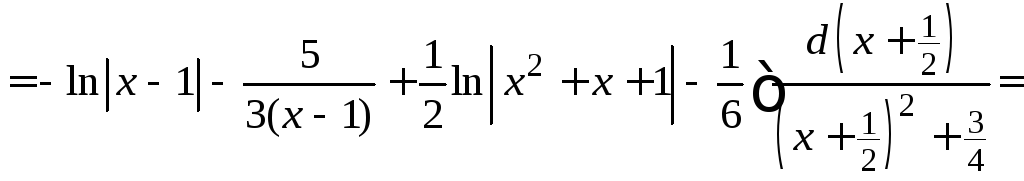
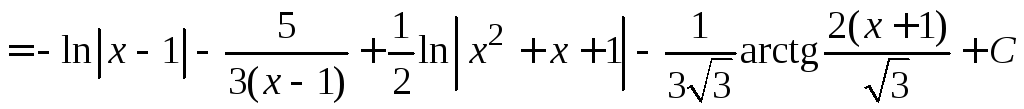Пример 4.26. Найти интеграл .

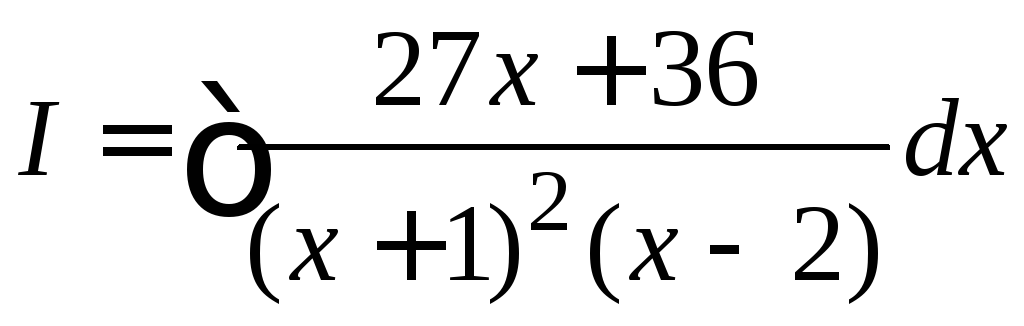Разлагаем подынтегральную функцию на простые дроби

.

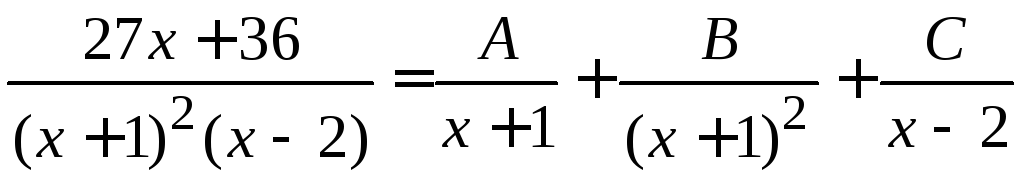Приравниваем числители дробей

.

Составляем систему для нахождения неопределенных коэффициентов.

В последнее равенство подставляем различные значения х, получаем

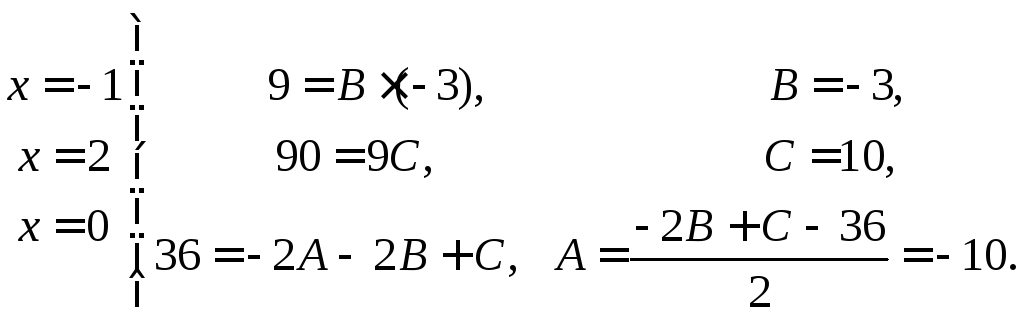
Находим интеграл

.
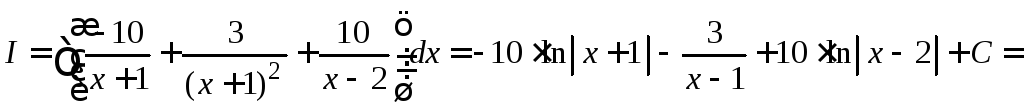
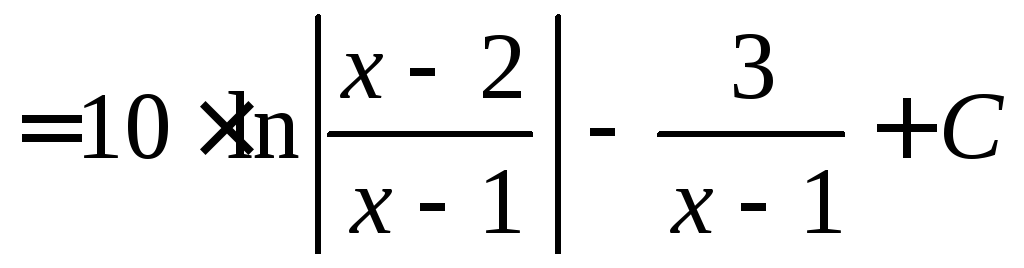