4.2. Свойства неопределенного интеграла

1. Производная неопределенного интеграла равняется подынтегральной функции, т. е.

.

Это свойство используется для проверки правильности интегрирования.

2. Дифференциал неопределенного интеграла равняется подынтегральному выражению

.

3. Интеграл от дифференциала функции равняется сумме этой функции и постоянной .

Действительно .

4. Постоянный множитель можно выносить из-под знака интеграла, т. е.

.

Проверим справедливость этого равенства. Найдем производные функций, стоящих в левой и правой частях равенства.

и .

5. Интеграл суммы функций равняется сумме интегралов этих функций

.

Справедливость этого равенства проверим так же, как в предыдущем свойстве.

, .

6. Вид интеграла не изменится, если переменную интегрирования заменить дифференцируемой функцией, т. е. если , то

,

где  дифференцируемая функция.

Проверим это дифференцированием. Найдем производную

.

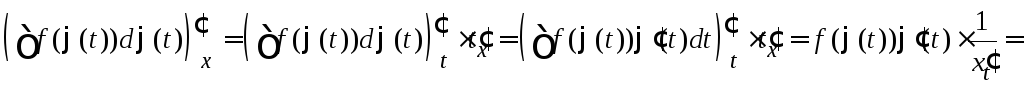
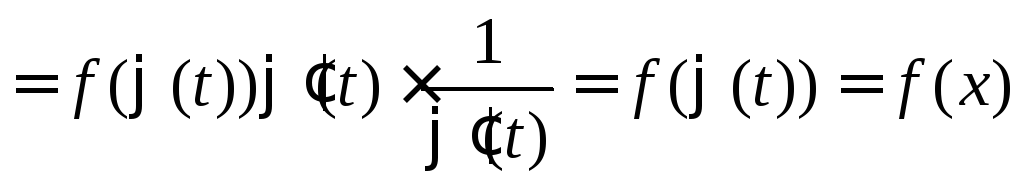6а. В частном случае, если в интеграле заменитьх на , то. Получим,

.

Например, если 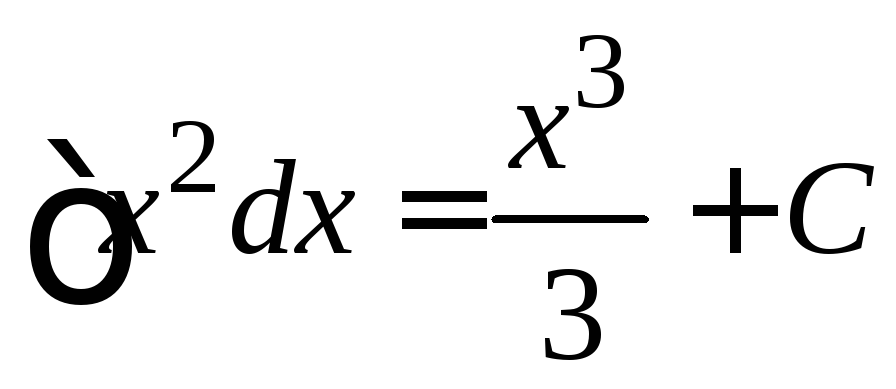, то;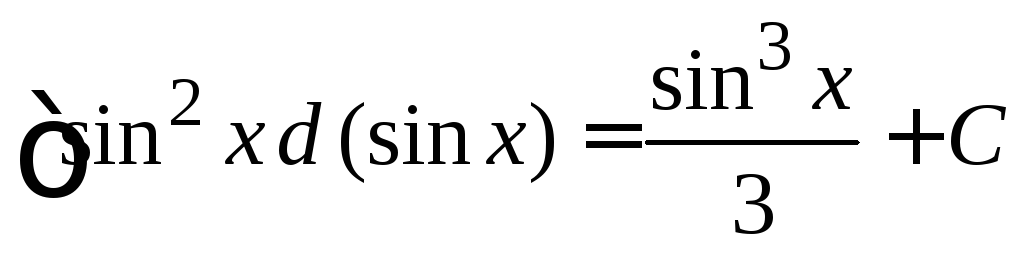

.

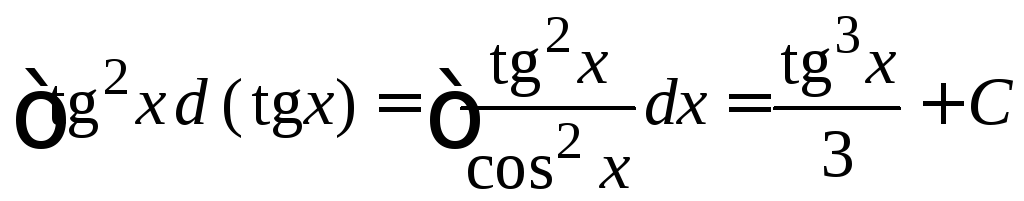Составим таблицу интегралов. Правильность табличных формул нетрудно проверить дифференцированием.

Таблица интегралов

1.	.	9.	.
2.	.	10.	.
3.	.	11.	.
4.	.	12.
5.	.	13.
6.	.	14.	.
7.	.	15.	.
8.	.

4.3. Методы интегрирования

4.3.1. Метод непосредственного интегрирования

Данный метод основывается на использовании таблицы и свойств интегралов.

Рассмотрим примеры применения данного метода. Найти интегралы.

Пример 4.1. .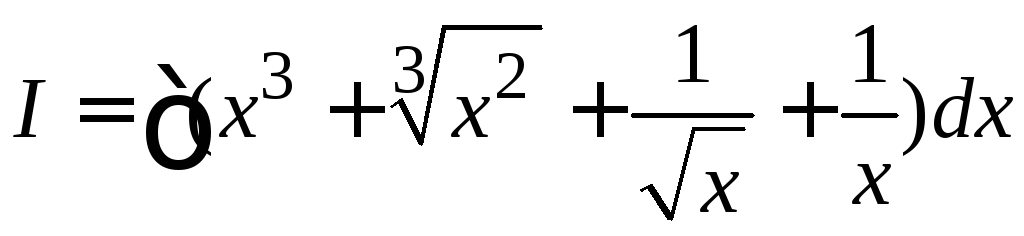

Запишем под интегралом переменную х с дробными показателями степени и используем табличные формулы №№ 2 и 3.

.

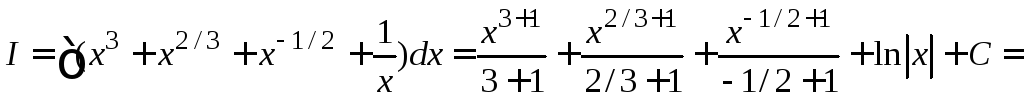
Пример 4.2. .

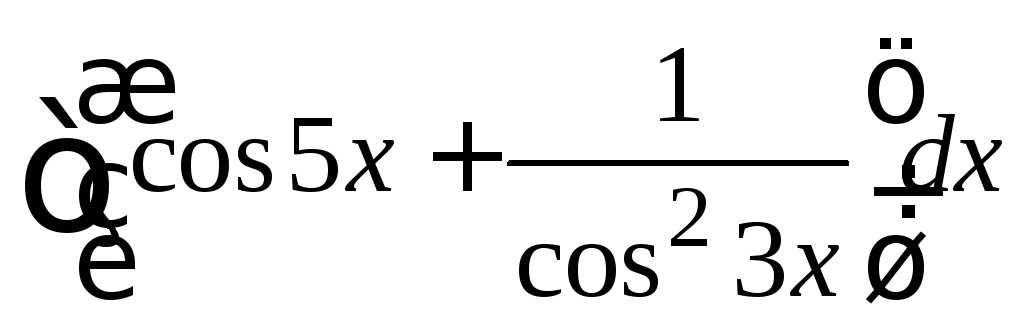Используем свойство 6а и табличные формулы №№ 7, 10.

.

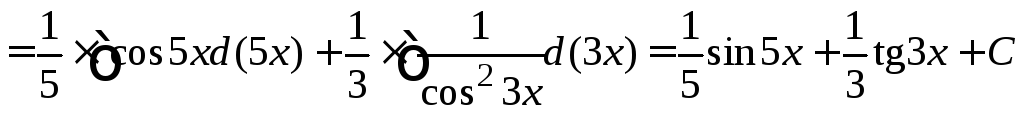Пример 4.3. .

Используем тригонометрические формулы, преобразуем подынтегральную функцию и применим табличные формулы №№ 8, 9.

.

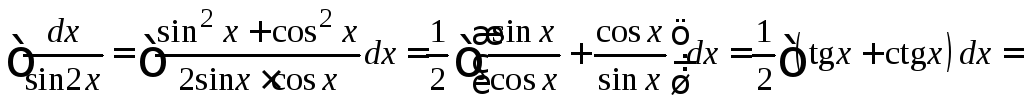
Пример 4.4. . Применили свойство № 6.

Пример 4.5. .

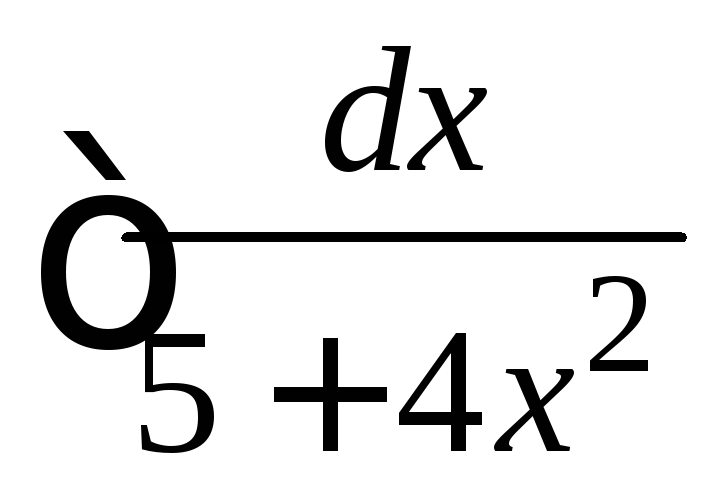Приведем интеграл к табличному виду. Для этого коэффициент 4 перед в знаменателе вынесем за знак интеграла. Затем применим формулу № 13.

.

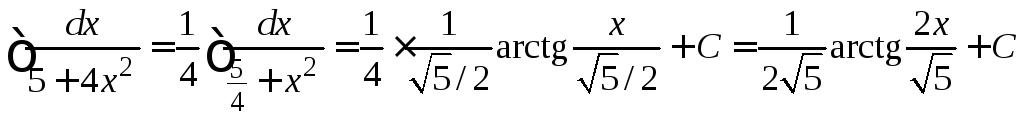Пример 4.6. .

Здесь также, как в предыдущем примере, вынесли коэффициент перед за знак интеграла и применили формулу № 15.

4.3.2. Метод замены переменной

Данный метод является основным универсальным методом интегрирования. Для его применения необходимо для заданного интеграла

подобрать дифференцируемую функцию и произвести под интегралом замену переменной

.

Если после замены переменной удается найти интеграл, то производится обратная замена . При этом, как показано выше (свойство 6), производная последнего интеграла, равняется подынтегральной функции

.

Иначе, необходимо либо выполнить другую подстановку, либо применить другой метод интегрирования. Для успешного применения метода замены переменной необходимо приобретать опыт интегрирования.

Пример 4.7.

.

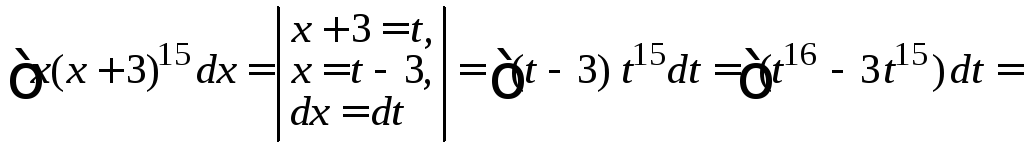
Пример 4.8.

.

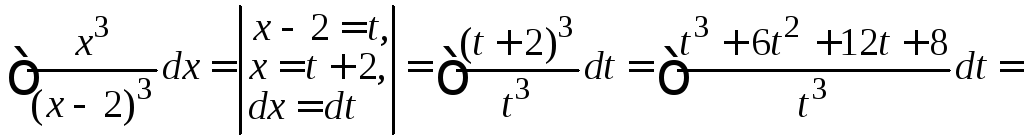
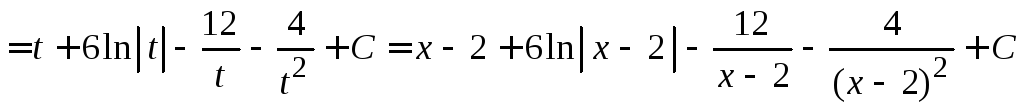Пример 4.9.

.

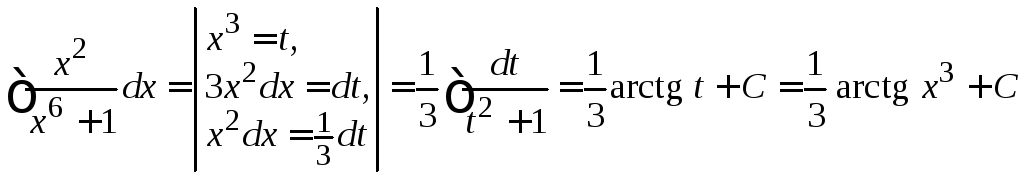Пример 4.10.

.

Пример 4.11.

.

Пример 4.12. .

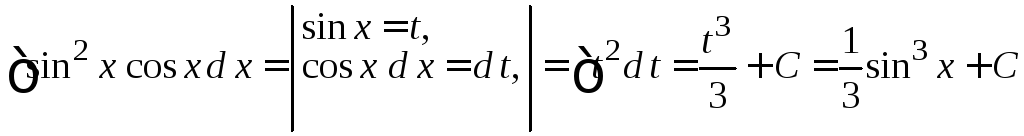Пример 4.13.

.

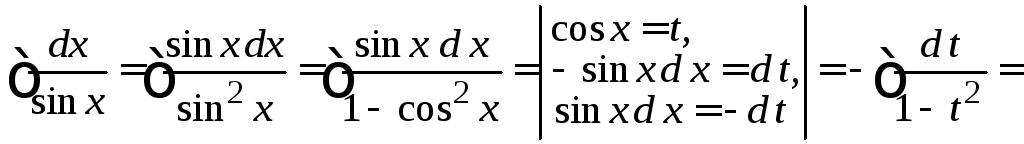
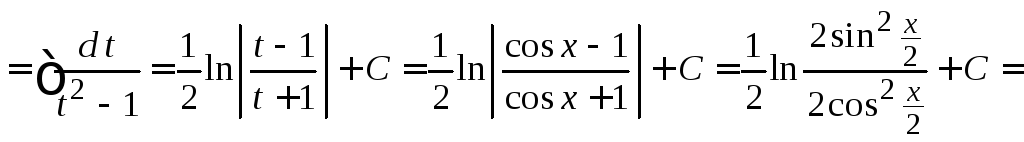
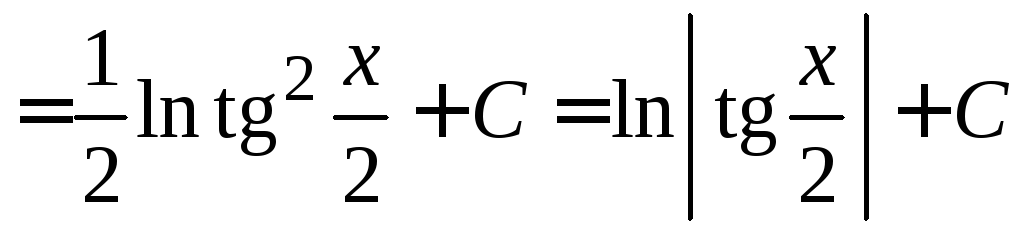Часто встречаются интегралы, которые легко приводятся к интегралу вида

.

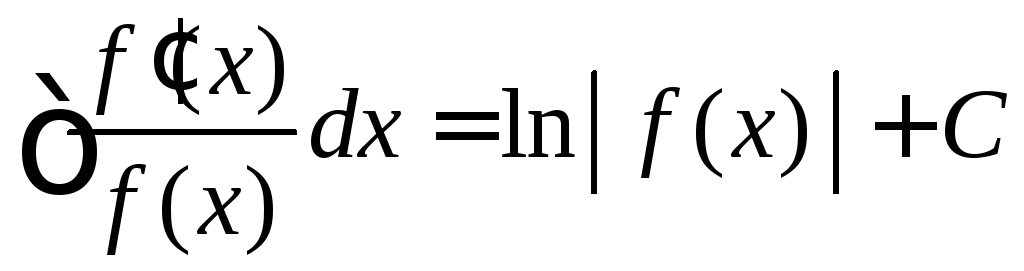Пример 4.14. .

Пример 4.15. .

Пример 4.16. .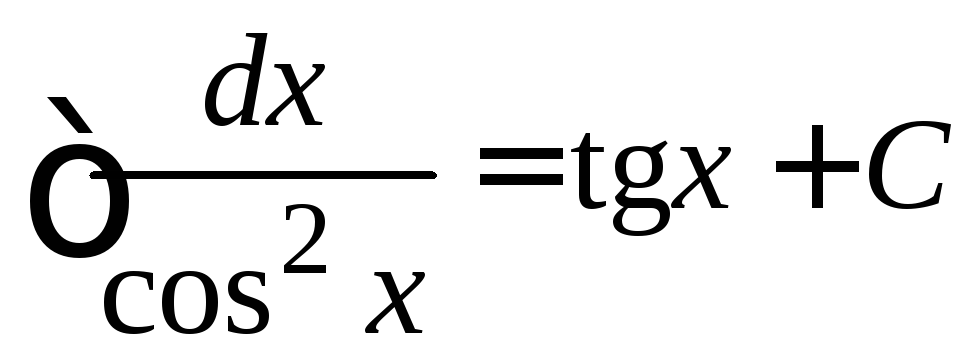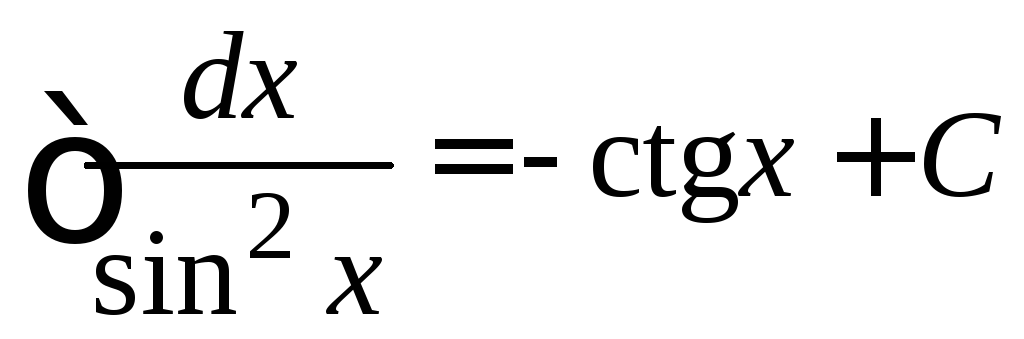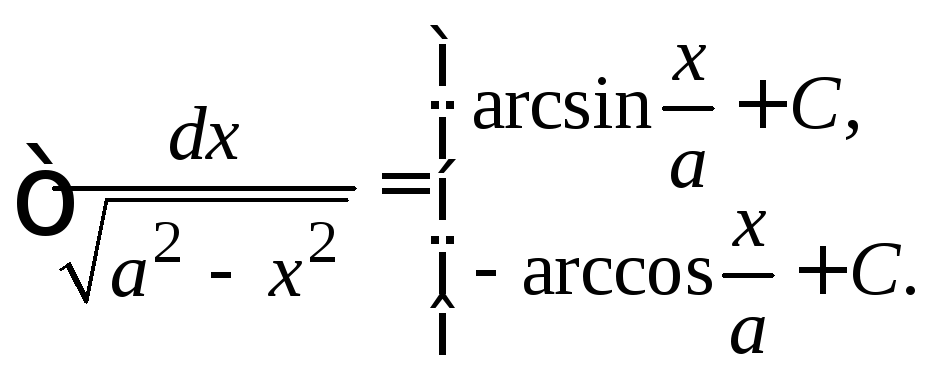
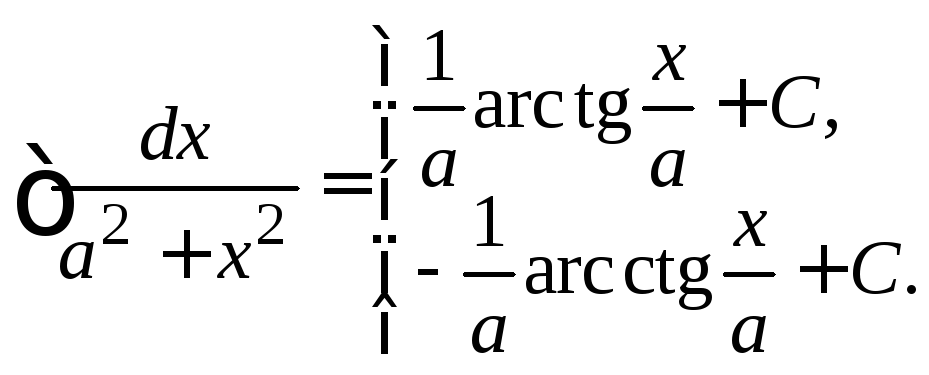
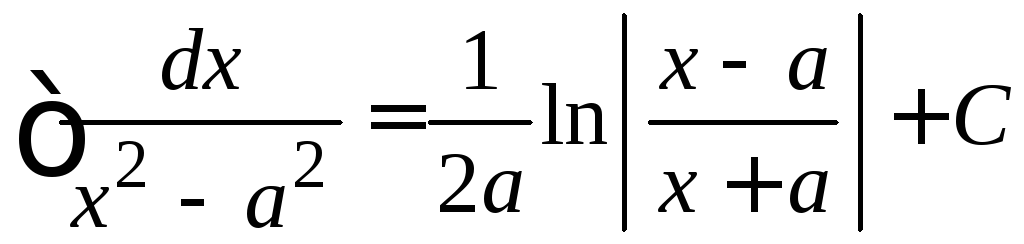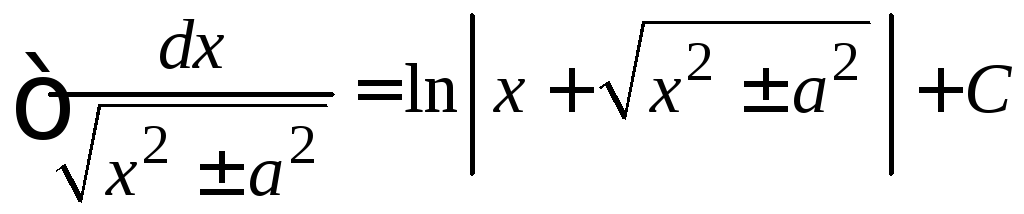