
- •В. Г. Шершнев математический анализ
- •Часть 2. Интегральное исчисление
- •Оглавление
- •Календарно-тематический план Распределение часов по темам и видам работ
- •Глава 4. Неопределенный интеграл
- •4.1. Определение неопределенного интеграла
- •4.2. Свойства неопределенного интеграла
- •4.3. Методы интегрирования
- •4.3.1. Метод непосредственного интегрирования
- •4.3.2. Метод замены переменной
- •4.3.3. Интегрирование функций, содержащих квадратный трехчлен
- •4.3.4. Метод интегрирования по частям неопределенных интегралов
- •4.3.5. Интегрирование дробно-рациональных функций
- •4.3.6. Об интегрировании простых дробей
- •4.3.7. Интегрирование иррациональных функций
- •4.3.8. Интегрирование тригонометрических функций
- •4.3.9. Интегрирование иррациональных функций с помощью тригонометрических подстановок
- •4.4. Об интегрировании в конечном виде
4.3.6. Об интегрировании простых дробей
После разложения правильной дробно-рациональной функции на простые дроби, для нахождения интеграла может потребоваться найти интегралы четырех типов:
1)![]() ;
2)
;
2) ,
(k
> 1); 3)
,
(k
> 1); 3)
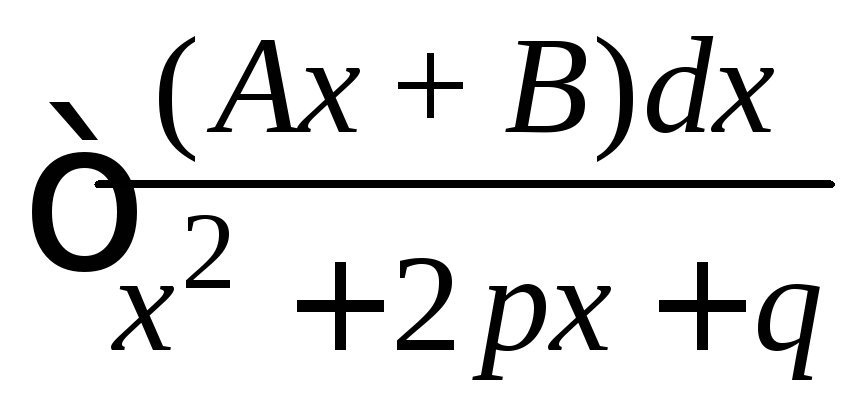 ;
4)
;
4)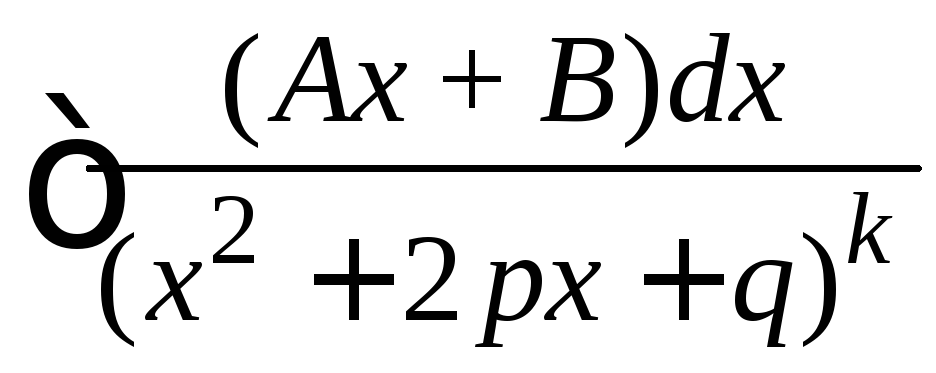 ,
(k
> 1).
,
(k
> 1).
При
этом квадратный трехчлен в 3-ем и 4-ом
интегралах не имеет вещественных корней,
так что
![]() .
.
Интегралы 1) и 2) легко находятся:
1)
![]() ;
2)
;
2)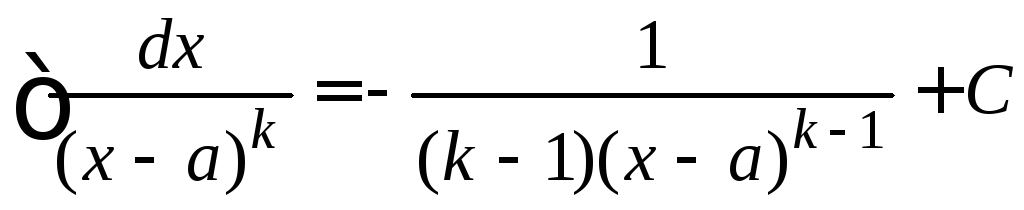 ,
(k
> 1);
,
(k
> 1);
Нахождение интегралов третьего типа рассмотрено ранее.
Рассмотрим нахождение интеграла четвертого типа.
Чтобы
устранить переменную х
в числителе, сформируем в числителе
производную квадратного трехчлена
![]() и получим два интеграла, один из которых
будет табличным, а другой без переменнойх
в числителе.
и получим два интеграла, один из которых
будет табличным, а другой без переменнойх
в числителе.
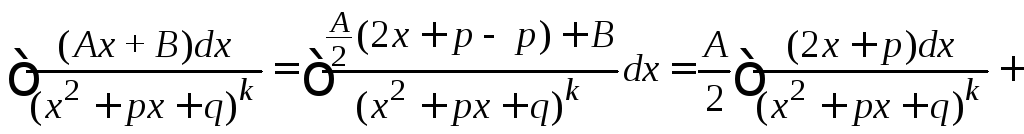
 ,
,
где
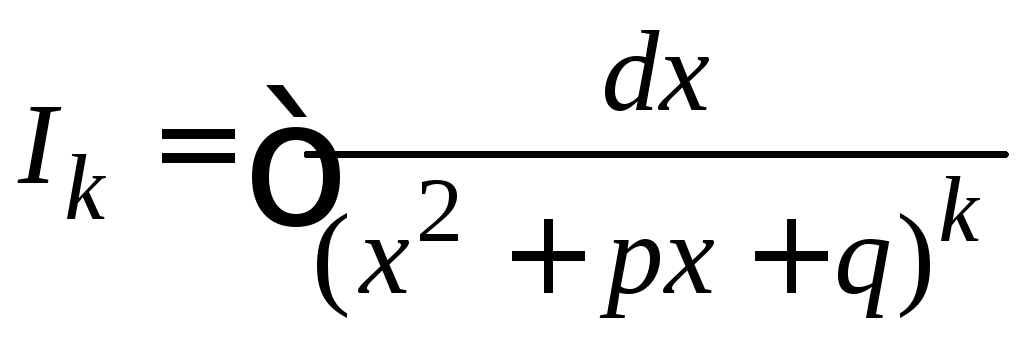 .
.
Получим
рекуррентную формулу для вычисления
интеграла
![]() .
В квадратном трехчлене выделим полный
квадрат и сделаем замену переменной.
.
В квадратном трехчлене выделим полный
квадрат и сделаем замену переменной.
 .
.
Интеграл
умножим и поделим на
![]() .
В числителе подынтегральной дроби
добавим и вычтем
.
В числителе подынтегральной дроби
добавим и вычтем![]() .
Разобьем интеграл
.
Разобьем интеграл![]() на два интеграла. Первый из получающихся
интегралов
на два интеграла. Первый из получающихся
интегралов![]() того же типа, что и
того же типа, что и![]() ,
только степень в знаменателе на единицу
меньше. Второй интеграл можно найти по
частям. Найдем
,
только степень в знаменателе на единицу
меньше. Второй интеграл можно найти по
частям. Найдем
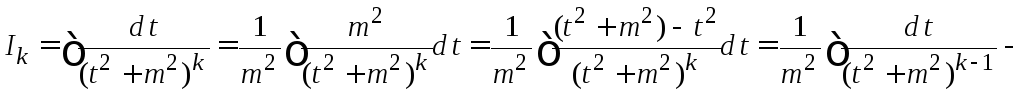
 .
.
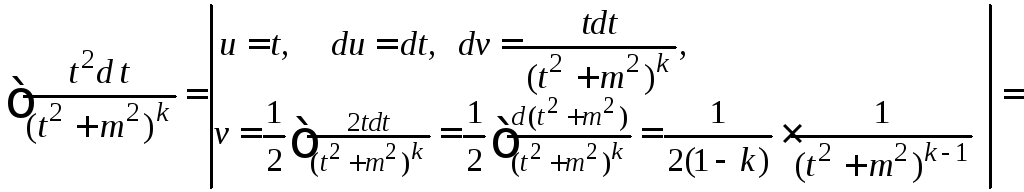
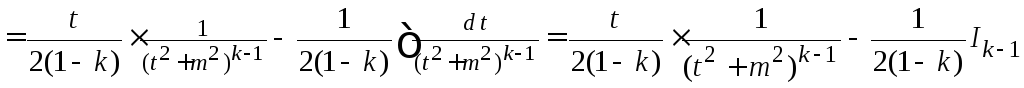 .
.
Тогда
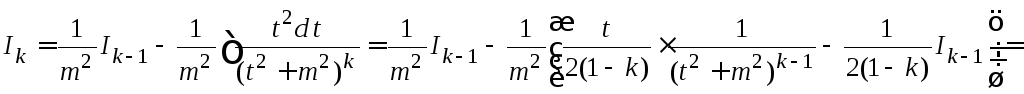
 .
.
Окончательно, получим рекуррентную формулу
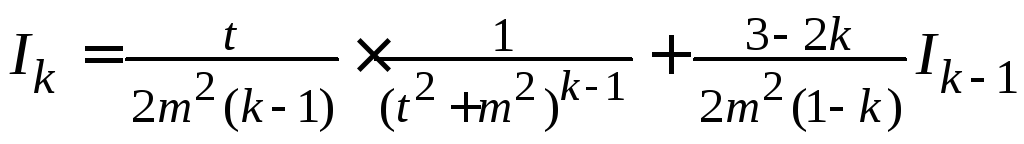 .
.
Пример
4 27. Найти
интеграл
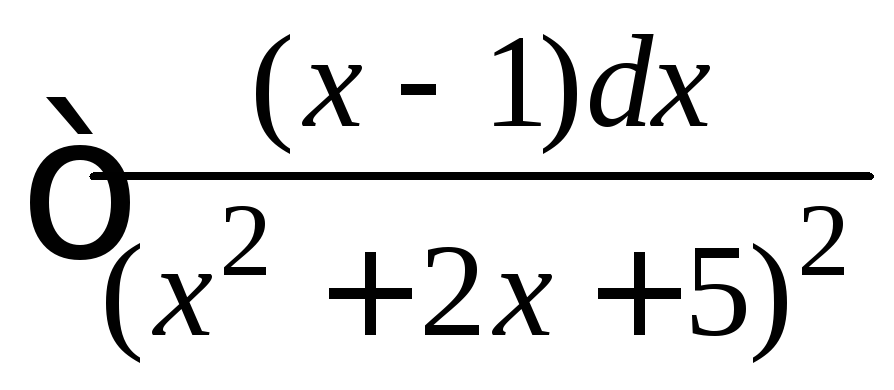 .
.
В
числителе подынтегральной функции
сформируем производную знаменателя
(![]() )
и разобьем интеграл на два интеграла
)
и разобьем интеграл на два интеграла
 .
.
Один интеграл найдем с помощью замены переменной
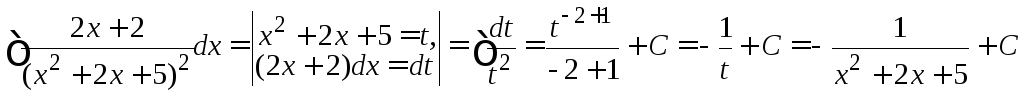 .
.
В другом интеграле также сделаем замену переменной и разобьем на два интеграла, получим
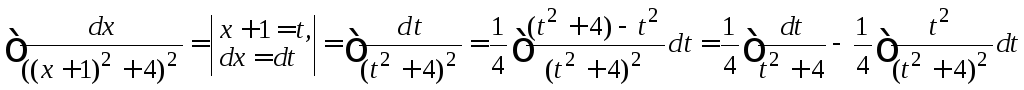 .
.
.Здесь
первый интеграл равен
 .
.
Второй интеграл найдем, используя метод интегрирования по частям.
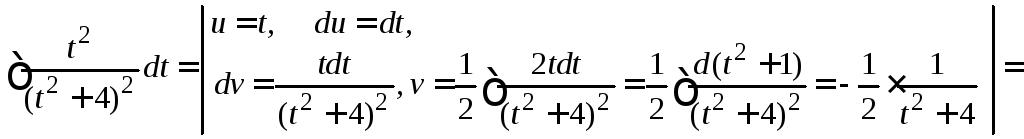
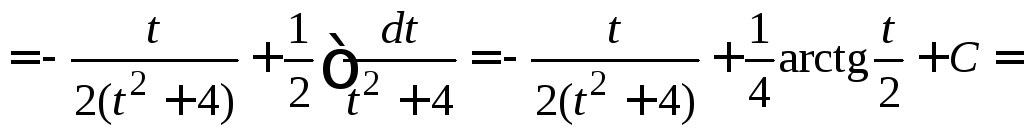
 .
.
Тогда интеграл
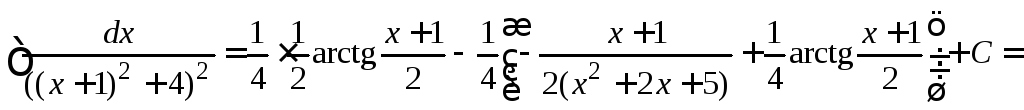
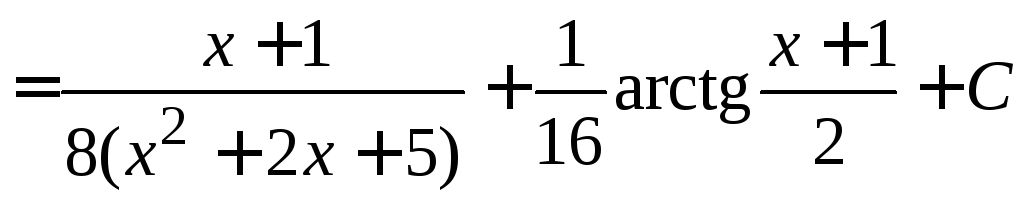 .
.
Найдем исходный интеграл
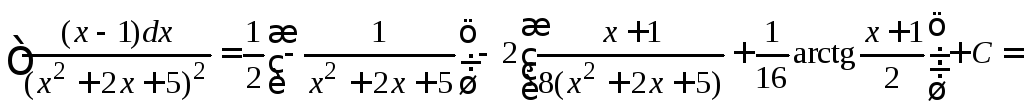
 .
.
4.3.7. Интегрирование иррациональных функций
Интегралы от иррациональных функций сводят с помощью подходящих замен к интегралам от рациональных функций.
Рассмотрим некоторые из возможных замен переменных, позволяющие свести интегралы от иррациональных функций к интегралам от рациональных функций.
I.
Интегралы
вида
![]() ,
гдеR
рациональная функция от иррациональных
выражений вида:
,
гдеR
рациональная функция от иррациональных
выражений вида:
![]() .
.
В
данном случае необходимо применить
подстановку
![]() ,
гдеn
общий знаменатель дробей
,
гдеn
общий знаменатель дробей
![]() .
Тогда
.
Тогда![]() .
.
Пример
4.28. Найти
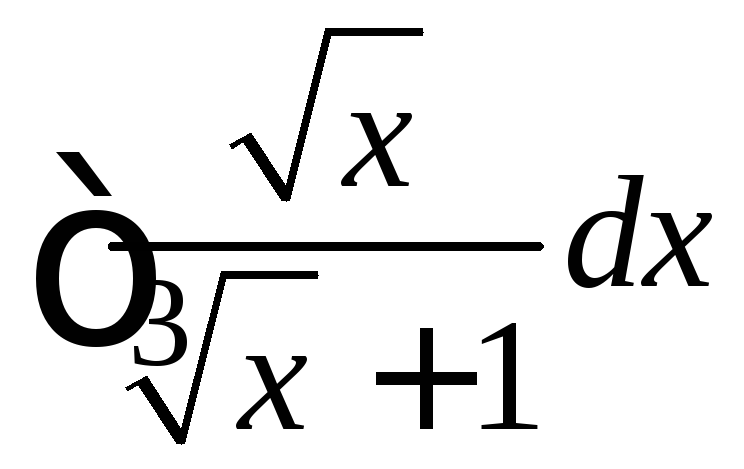 .
.
Выполняем замену переменной, находим
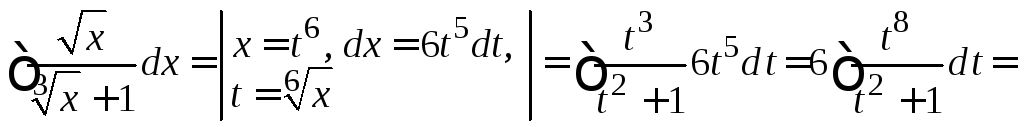
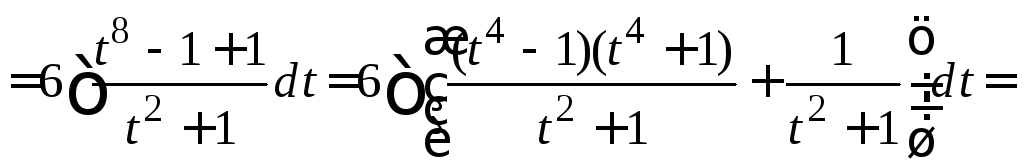
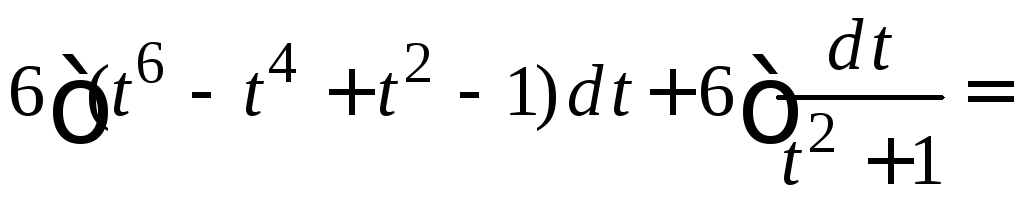
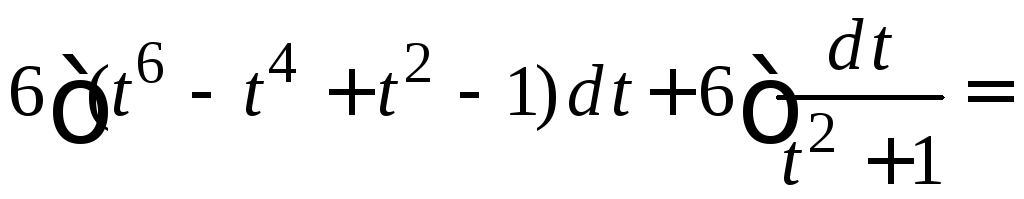
![]()
![]() .
.
II.
Интегралы
вида
 .
.
В
этом случае необходимо применить
подстановку
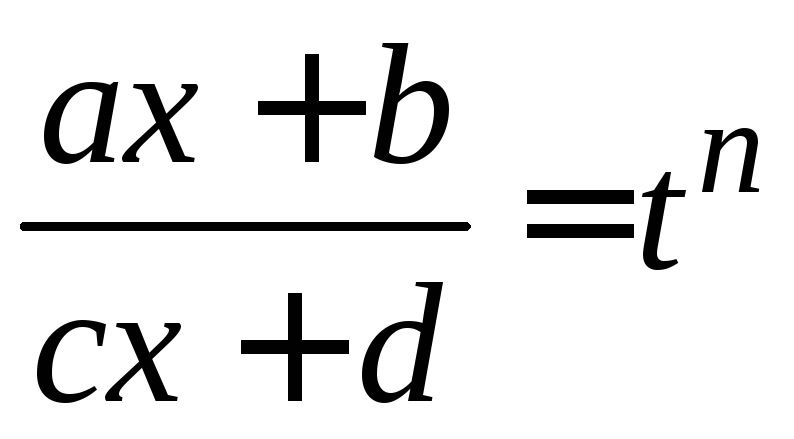 ,
гдеn
– общий
знаменатель дробей
,
гдеn
– общий
знаменатель дробей
![]() .
.
Пример
4.29. Найти
 .
.
Подстановка
![]() .
Отсюда
.
Отсюда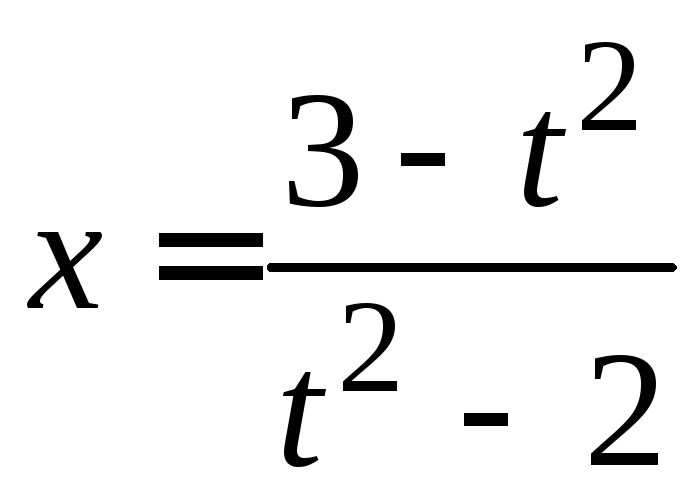 ,
, ,
,
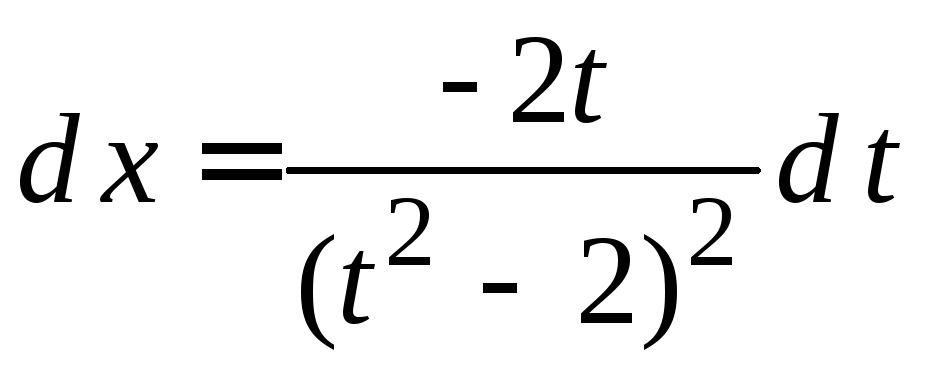 ,
,
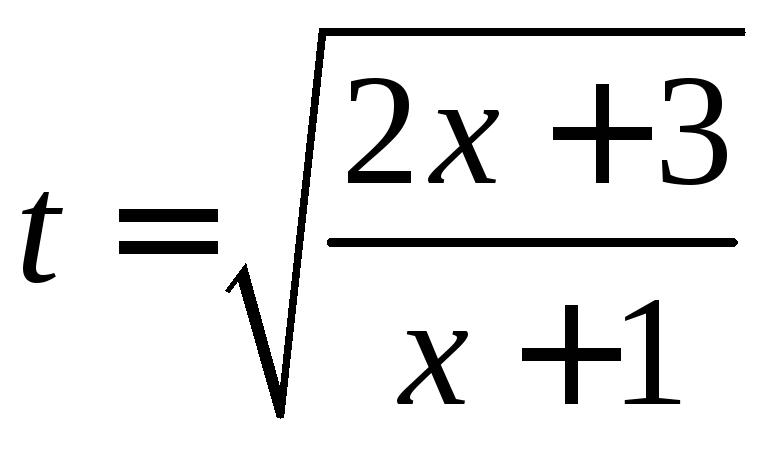 .
.
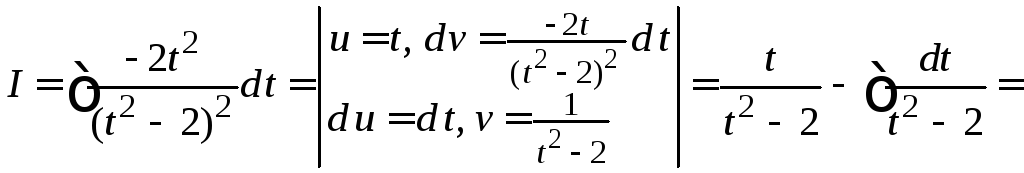
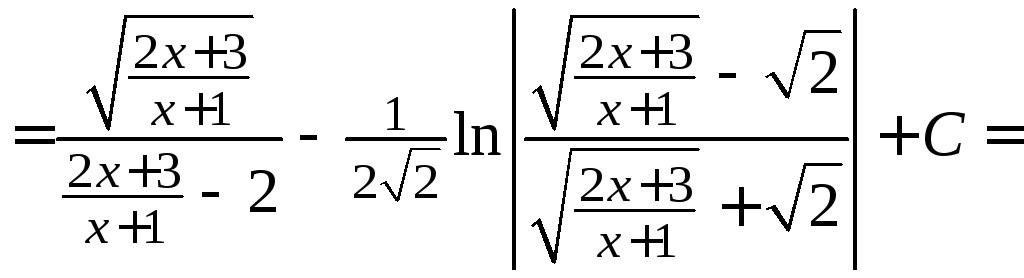
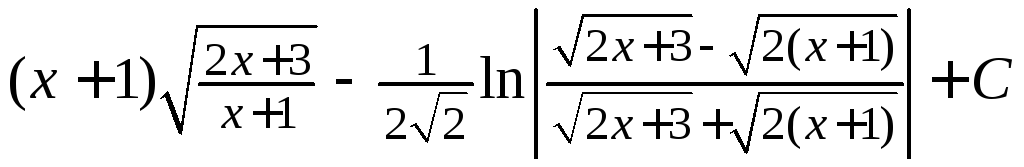 .
.
III.
Три подстановки
Эйлера для интеграла![]() ,
где R
рациональная функция,
,
где R
рациональная функция,
![]() .
.
1.
Первая подстановка Эйлера
![]() .
.
Примем
знак + перед
![]() и возведем в квадрат. Получим
и возведем в квадрат. Получим
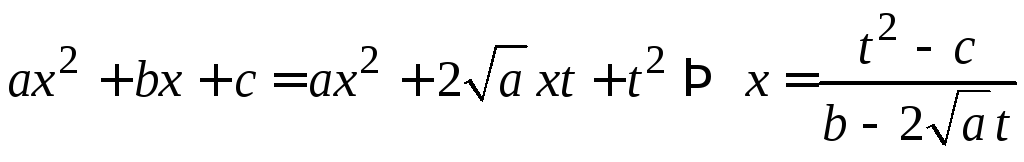 .
.
Тогда
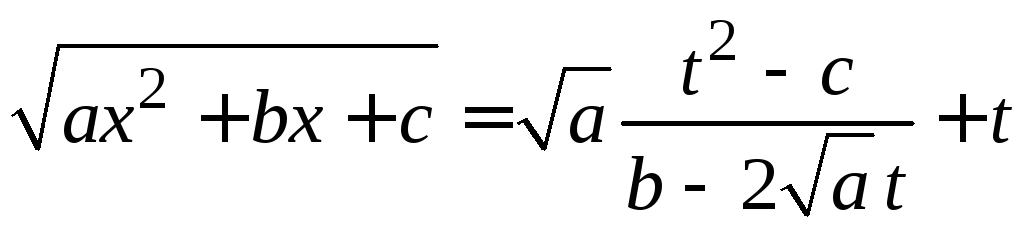
рациональное выражение и интеграл
приводится к интегралу от рациональной
функции.
рациональное выражение и интеграл
приводится к интегралу от рациональной
функции.
Пример
4.30. Найти
![]() .
.
Применим
подстановку ![]() .
.
Тогда
![]()
 .
.
![]()
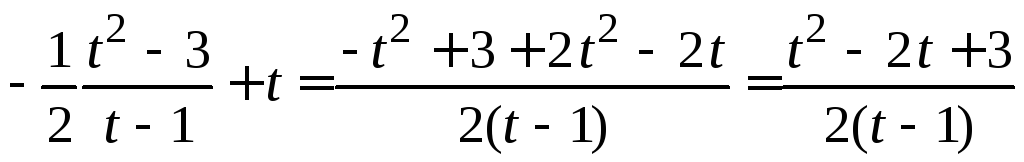 .
.
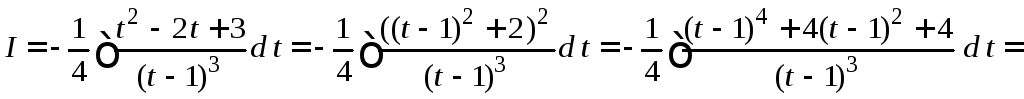
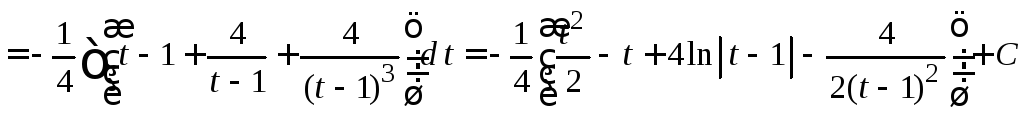 =
=
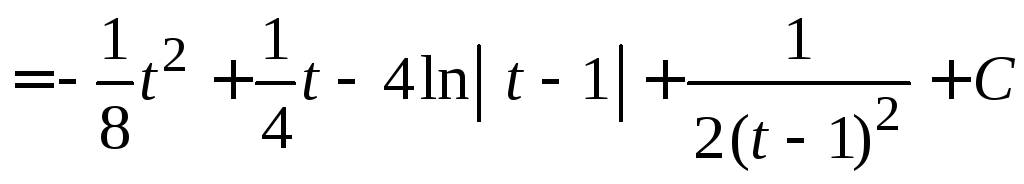 ,
где
,
где
![]() .
.
2.
Вторая подстановка Эйлера имеет вид
![]()
Если
принять знак + перед
![]() ,
то после возведения в квадрат получим
,
то после возведения в квадрат получим
![]()
![]()
 .
.
 .
.
Таким
образом,
![]() иdx
будут рациональными выражениями и
интеграл будет от рациональной функции.
иdx
будут рациональными выражениями и
интеграл будет от рациональной функции.
3. Третья подстановка Эйлера используется в случае, когда квадратный трехчлен под корнем имеет вещественные корни и
![]() .
.
Подстановка
имеет вид
![]() .
.
![]()
 .
.
Пример
4.31. Найти
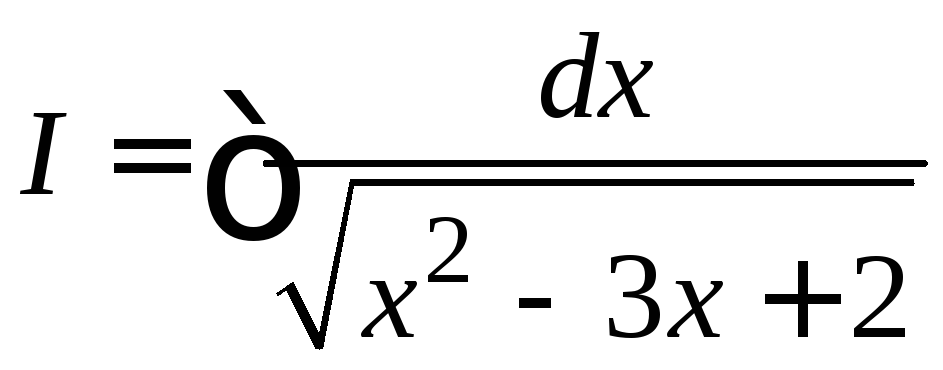 .
.
![]() ;
;
![]() ;
;
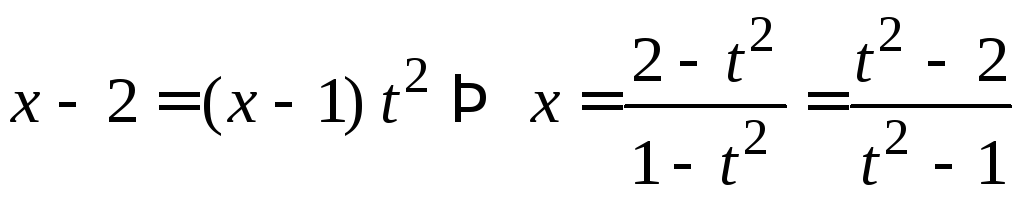 ;
;
 ;
;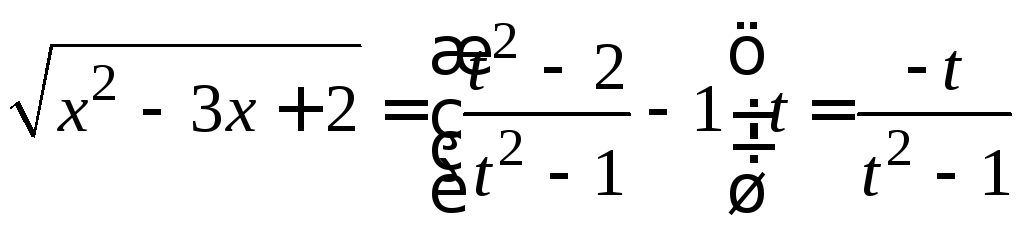 .
.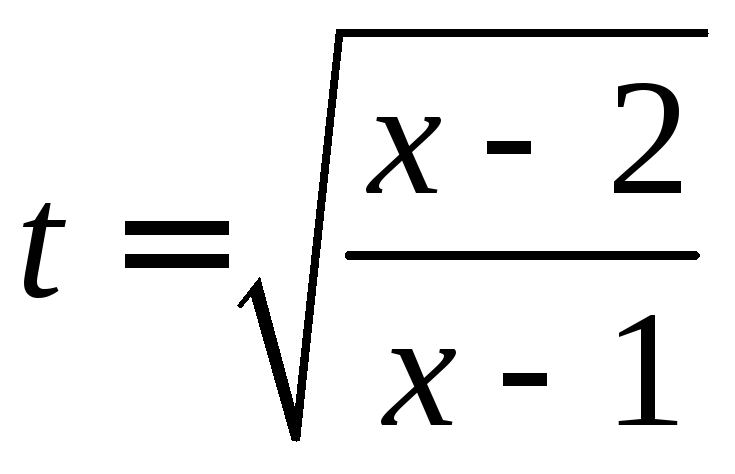 .
.
 =
=
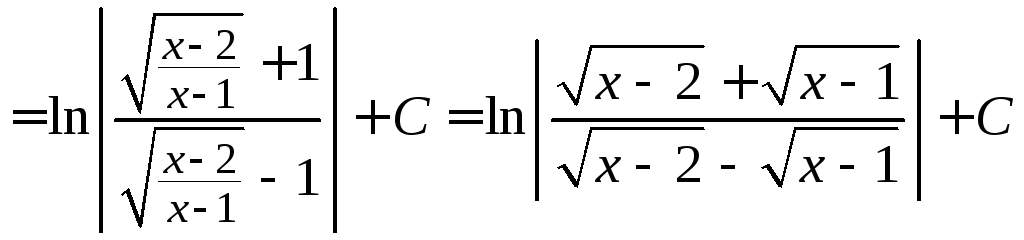 .
.
