3.5.8 Колебательное звено второго порядка

Операторный коэффициент передачи

(3.60)

При корни знаменателя комплексные:параметр затухания переходного процесса;q – частота свободных колебаний.

Найдем выражения для переходной функции. По определению аналитическим выражением переходной функции является решение уравнения (3.34) при нулевых начальных условиях. Тогда, используя преобразование Лапласа

=

Переходя к оригиналу, получим

h(t) =1(t), (3.61)

где

Найдем выражение для частотной передаточной функции. Для этого заменим в передаточной функции (3.60) s на j

()

Амплитудно-частотная характеристика колебательного звена

(3.62)

Фазочастотная характеристика инерционного звена

(3.63)

С помощью перечисленных элементарных звеньев первого порядка можно представить передаточные функции подавляющего большинства физически реализуемых радиоэлектронных устройств и систем.

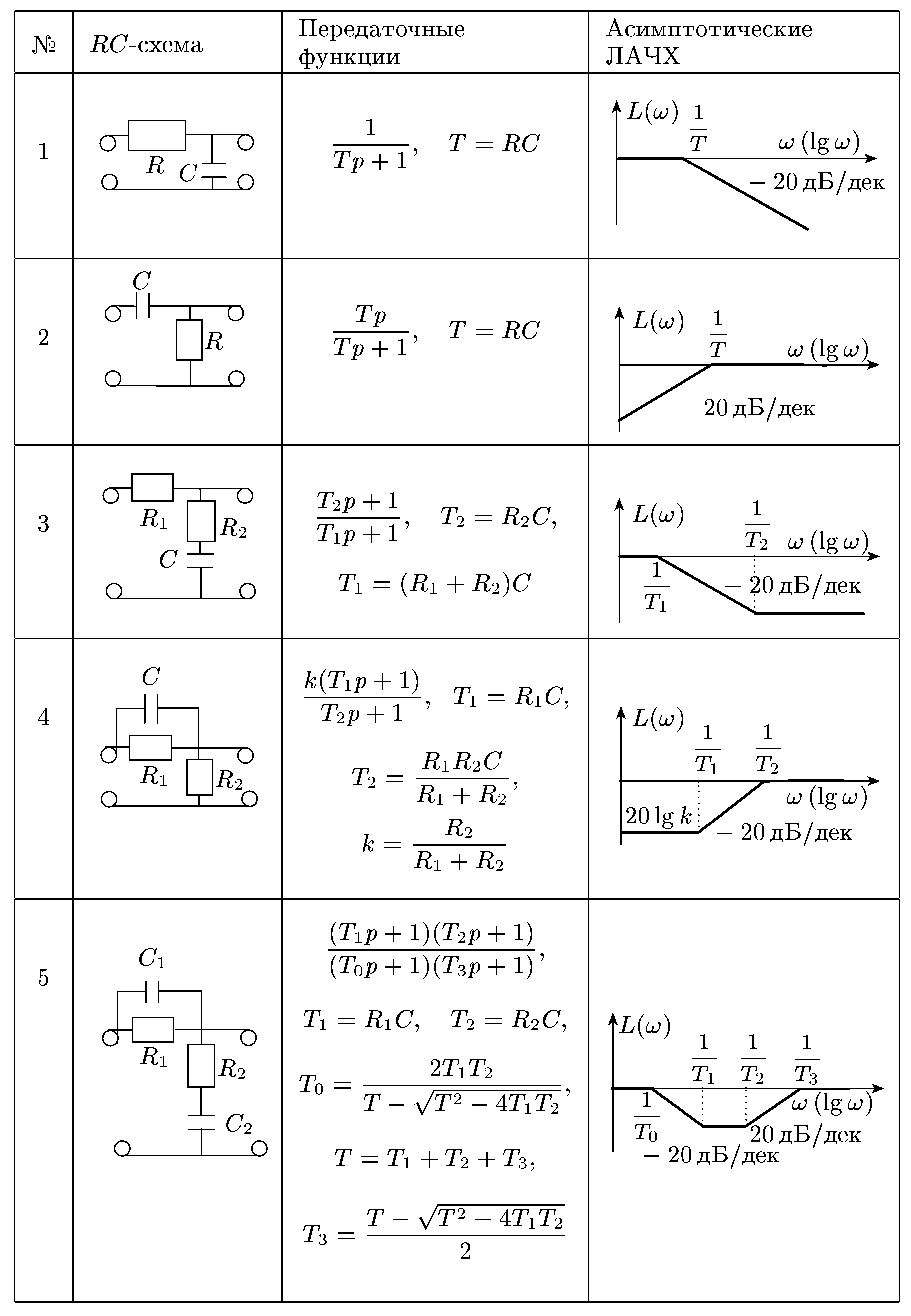
В приведенной ниже таблице представлены типовые динамические звенья и их передаточные функции.

№	Тип звена		Передаточная функция звена
1	Позиционные звенья	Безинерционное (усилитель)
2		Апериодическое звено 1-го порядка
3		Апериодическое звено 2-го порядка
6	Интегри- рующие звенья	Идеальное интегрирующее звено
7		Интегрирующее звено c замедлением
8		Изодромное звено
9	Дифференци-рующие звенья	Идеальное дифференцирующее звено
10		Дифференцирующее звено с замедлением

3.6 Устойчивость сар

Анализ устойчивости непосредственно связан с определением условий равновесия. В линейных системах существуют только одно состояние равновесия. Поэтому зависимые переменные, характеризующие состояние системы, с течением времени приближаются либо к состоянию покоя, либо периодического изменения.

Если достаточно малое (независимо от того, какими причинами оно вызвано) возмущение приводит к существенному отклонению режима от исходного (установившегося) состояния или от невозмущенного движения, то говорят о нестабильности или неустойчивости положения равновесия или невозмущенного движения. Если же после прекращения действия возмущения система не отклоняется существенно от своего исходного состояния, то такой режим называют устойчивым.

Значительным вкладом в теорию устойчивости явилось исследование выдающегося русского математика А. М. Ляпунова « Общая задача об устойчивости движения» (1892), которая еще и сегодня представляет собой основу всех исследований в этой области.

Методы анализа устойчивости линейных и линеаризованных систем.

Для определения устойчивости системы с обратной связью необходимо определение всех корней ее характеристического уравнения – всех до единого. Однако в системах высокого порядка вычисление корней весьма затруднительно. При этом часто приходится прибегать к численным методам, что еще более затрудняет задачу.

Чтобы избежать указанных трудностей и не вычислять вообще корней характеристического уравнения был разработан ряд методов, так называемых критериев устойчивости. При их помощи можно определить характер устойчивости или неустойчивости системы, не вычисляя корней характеристического уравнения.

Математическая формулировка условий, которым должны удовлетворять коэффициенты характеристического уравнения или какие-либо функции этих коэффициентов, чтобы система была устойчивой, называют критерием устойчивости.

В настоящее время известно множество критериев устойчивости, позволяющих решать задачу при различных, конкретных условиях. Таковы алгебраический критерий Гурвица, критерий Рауса, частотный критерий Найквиста с различными дальнейшими модификациями, например, Михайлова, и др.

Несмотря на формальное различие перечисленных критериев друг от друга, по сути все они основаны на известной теореме теории функций комплексного переменного, а именно, теореме Коши относительно числа нулей и полюсов функции, аналитической в заданной области.

Заметим, что частотные критерии позволяют судить об устойчивости замкнутых САР по частотным характеристикам условно разомкнутых САР без определения корней характеристического уравнения замкнутой системы. При этом необходимо знать, устойчива или нет условно разомкнутая система.

Критерий устойчивости Найквиста — Михайлова — один из способов судить об устойчивости замкнутой системы управления по амплитудно-фазовой частотной характеристике её разомкнутого состояния. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсов передаточной функции замкнутой системы.

Рассмотрим однокольцевую однокоординатную САР. Ее структурная схема приведена на рис.3.17:

(3.60)

где x_ВЫХ и x_ВХ - выходная и входная величины, K_ПРЯМОЕ(s) и K_{ОБРАТНОЕ}(s) передаточные функции цепей прямой передачи (от входа возмущающего воздействия к выходу САР) и отрицательной обратной связи (от выхода ко входу сигнала), а W(s) – коэффициент передачи разомкнутой САР; s (или p) - оператор Лапласа (s ≡), а знак плюс в знаменателе означает, что обратная связь отрицательная. Здесь j — комплексное число, характеризующее единичный вектор, а — угловая частота.

Проанализируем операторное характеристическое уравнение замкнутой системы (3.60):

(3.61)

в которое входит функция условно разомкнутой системы :

(3.62)

С учетом (3.11) выражение (3.62) можно переписать

и представить в виде:

(3.63)

где q_n и r_n – корни соответственно числителя и знаменателя уравнения (3.63). В общем случае корни q_n и r_n – комплексные числа.

Корни полинома числителя называют нулями, а корни знаменателя - полюсами. Положив в частном случае , получим, что начало векторабудет находиться в точке, а конец – на мнимой оси. При изменении ω от– ∞ до + ∞ этот конец будет перемещаться по мнимой оси из – ∞ в + ∞. Следовательно, вектор при изменении ω от– ∞ до + ∞ повернется на пол-оборота (на угол + π против часовой стрелки), если корень лежит слева от мнимой оси, и по часовой стрелке, если корень расположен справа от мнимой оси.

Поэтому полином (3.63) можно представить в виде векторов модули которых равны произведению модулей сомножителей, а фазы – сумме углов поворота всех векторов сомножителей числителя и знаменателя соответственно:

(3.64)

Для устойчивой замкнутой системы при изменении ω от – ∞ до + ∞ вектор числителя повернется на угол, а при изменении ω от 0 до + ∞ - на угол

Для того, чтобы система САР была устойчивой необходимо и достаточно, чтобы в знаменателе выражения (3.60), (в уравнении 1+ W(s) = 0) не было корней с положительными α, т.е. расположенных в правой полуплоскости комплексной частоты s. Сказанное аналогично и для уравнения (3.64).

В теории САР Г. Найквистом в 1932 году было доказано, что

– если система устойчива в разомкнутом состоянии, то для устойчивой работы системы в замкнутом состоянии необходимо и достаточно, чтобы АФХ разомкнутой системы для не охватывала точку с координатами (– 1, j0). Только в этом случае приращение аргумента вектора будет равно нулю;

– если система неустойчива в разомкнутом состоянии и имеет m корней в правой полуплоскости, то для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы для охватывалаm/2 раз точку с координатами (– 1, j0), т.е. приращение аргумента вектора должно составлять.

Действительно, чтобы САР была устойчивой, знаменатель выражения (3.60) не должен равняться нулю, т.е.или, в обозначениях фазовой плоскости (рис.3.5), не попадала в точку с координатами (– 1, j0); в противном случае система возбудится.

Применительно к логарифмическим ЛАХ и ЛФХ можно утверждать, что система будет устойчивой, если в области частот ω, где аргумент по абсолютному значению превышает π, модульбудет меньше единицы.

Сделаем еще одно важное замечание. Передаточную функцию, не имеющую нулей или полюсов в правой полуплоскости s, называют функцией минимальной фазы, а систему, имеющую такую передаточную функцию – системой минимально-фазового типа. Такое название обязано тому примечательному факту, что среди устойчивых систем с заданной АЧХ минимально-фазовая система имеет наименее возможное изменение фазового сдвига (наименьший набег фазы) при изменении частоты ω от нуля до бесконечности. К тому же в системах минимально-фазового типа АЧХ и ФЧХ имеют взаимно однозначную зависимость. Это означает, что если известна одна из указанных характеристик (частота или фаза), то другая (фаза или частота) может быть однозначно определена расчетным путем.

Для определения устойчивости замкнутой системы строится ЛАФЧХ разомкнутой системы (см. рис.3.17). После этого необходимо найти частоту среза ω₀, решив уравнение (здесь и далее), и частоту ω_φ — максимальную из частот, для которых Тогда— запас устойчивости по амплитуде (обычно требуется не менее 10 дБ),)— запас устойчивости по фазе (обычно требуется не менее 30°). Если эти запасы отрицательны, то замкнутая система неустойчива; если равны нулю — находится на границе устойчивости.

Например, пусть коэффициент K_ПРЯМОЕ(s) системы, показанной на рис. 3.17, состоит из трех активных апериодических звеньев вида (3.34), включенных последовательно:

а коэффициент K_{ОБРАТНОЕ}(s) = β = const, причем Построим ЛАХ и ЛФХ для случая разомкнутой системы – отсутствияK_{ОБРАТНОЕ}(s) – рис.3.18.

В данном примере k₁ = 48дБ, k₂ = 36дБ, k₃ = 12дБ; lg(k₀) = lg(k₁)+lg(k₂) + lg(k₃) = 96дБ; f₁ = 10Гц, f₂ = 1кГц, f₃ = 100кГц. Это типичная АЧХ трехкаскадного операционного усилителя без коррекции. Частота единичного усиления f₀ = 25кГц, а коэффициент усиления на постоянном токе равен 96дБ.

Усилитель неустойчив, поскольку фазовый набег на частоту единичного усиления f₀ составляет φ₀ = – arctg(f₀/f₁) – arctg(f₀/f₂) – arctg(f₀/f₃) = – 90º – 87,7º – 14º = – 191,7º и запас по фазе ) отрицательный а коэффициент усиления на частоте f_φ, на который фазовый сдвиг будет минус 180º равен примерно +19дБ. Иными словами, для достижения границы устойчивости необходимо уменьшить фазовый набег на частоту единичного усиления f₀ на 11,7º (а с учетом запаса по фазе 30º – на 41,7º) или уменьшить коэффициент усиления на частоте f_φ на 19дБ (а с учетом запаса по амплитуде – на 29дБ).

Если нет требований к сохранению исходной полосы пропускания, можно поступить следующим образом: уменьшить коэффициент усиления введением низкочастотного корректирующего ПИФ и ввести компенсацию второго интегрирующего звена исходного ОУ с помощью корректирующего ПДФ. Чтобы усилитель был устойчив в диапазоне эксплуатационных воздействий, необходимо обеспечить на новой частоте единичного усиления f₀ = 6кГц запас по фазе не менее 30º (фазовый сдвиг не более 150º). Возможный вариант коррекции приведен на рис.3.19.

На новой частоте среза фазовый набег составит:

Зеленым цветом на рис. 3.19 показана исходная ЛАХ неустойчивого ОУ, красным цветом показана желаемая ЛАХ, черным цветом – ЛАХ корректирующих цепей. Очевидно, что в интервале частот f₀₁ – f₀₂ работает ПИФ, корректируя первый излом ОУ на частоте f₁, в интервале частот f₀₃ – f₀₄ работает ПДФ, корректируя изломы на частотах f₂ и f₃. Коррекция получилась достаточно простой, запас по фазе велик и равен

Следует помнить, что при указанном подходе – компенсации изломов исходной АЧХ на частотах f₁, f₂, f₃ – следует предъявлять достаточно жесткие требования к точности совпадения частот f₁ и f₀₂, f₂ и f₀₃, f₃ и f₀₄. При несовпадении частот указанных пар образуются т. наз. «дуплеты», которые приводят к затягиванию времени переходного процесса; при этом в статическом режиме неравномерность АЧХ будет минимальной.

При необходимости сохранения частоты единичного усиления f₀ возможна более сложная коррекция ЛАХ – рис.3.20. При такой коррекции достигается фазовый сдвиг на частоте единичного усиления не более

Запас по фазе достаточно большой, поэтому можно упростить корректирующую цепь, исключив дифференцирующий участокf₃ - f₀₀₃ (на рис.3.20 показано пунктиром). Отрицательный фазовый сдвиг увеличится на , это приведет к такому же уменьшению запаса по фазечто вполне приемлемо.

Сложность при коррекции как по первому, так и по второму варианту заключается в обеспечении дополнительного усиления вследствие «дифференцирующей» коррекции в диапазоне частот (f₀₃ - f₀₄ на рис.3.19) и (f₀₂ - f₀₃ - f₀₀₄ на рис.3.20), что может потребовать введения дополнительного звена активного фильтра.

Характеристики каскада, собранного на идеальном ОУ определяются внешней схемной обвязкой ОУ и не зависят от других факторов. Другими словами, отрицательная обратная связь (ООС) полностью определяет свойства электрической схемы с идеальным ОУ. Принцип введения отрицательной обратной связи в ОУ иллюстрирует рис. 3.21.

Часть U_ОС выходного напряжения U_ВЫХ возвращают через цепь обратной связи с коэффициентом передачи β < 1 ко входу усилителя. Если, как это показано на рис. 3.6, напряжение обратной связи вычитают из входного напряжения, обратную связь называют отрицательной (ООС). В усилительных каскадах используют, как правило, отрицательную обратную связь.

После достижения устойчивого состояния (после завершения переходных процессов) выходное напряжение ОУ

U_ВЫХ = A₀U_ДФ = A₀(U_ВХ – U_ОС) = A₀(U_ВХ – β U_ВЫХ).

Решив это уравнение относительно U_ВЫХ, получим:

      (3.65)

При A₀ → ∞ коэффициент усиления ОУ, охваченного обратной связью составит

(3.66)

Таким образом, из (3.66) следует, что коэффициент усиления ОУ с обратной связью определяет почти исключительно величина обратной связи β и он мало зависит от параметров самого усилителя.

В простейшем случае цепь обратной связи представляет собой резистивный делитель напряжения. При этом схема с ОУ работает как линейный усилитель, коэффициент усиления которого определяет только коэффициент обратной связи β.

Следует помнить, что любой усилитель обладает не только ограниченным коэффициентом усиления, но и ограниченной полосой пропускания. Как правило, подавляющее большинство ОУ имеют цепь внутренней частотной коррекции (см. табл.1 для AD820) и их следует представлять в виде инерционного (интегрирующего) звена с коэффициентом усиления A₀.

Сказанное иллюстрирует рис. 3.22, на котором приведена АЧХ ОУ AD8065. Из рисунка ясно видно, что ОУ имеет цепь внутренней коррекции (интегрирующее звено), поскольку фазовый сдвиг выходного сигнала относительно входного в диапазоне частот примерно 1кГц…20МГц составляет приблизительно 90°. Этот факт необходимо учитывать при построении ФЧХ устройств, собранных на ОУ AD8065.

Следует также помнить, что наклонная линия GAIN на рис.3.22 характеризует предельные возможности данного ОУ – за пределы этой линии АЧХ усилительных устройств, собранных на основе AD8065, не выйдут ни при каких обстоятельствах. В качестве иллюстрации сказанного посмотрим на рис.3.23. Спады частотных характеристик примерно соответствуют линии GAIN рис.3.20.

Рис.3.22

Рис.3.23

Если в качестве цепи ООС применить цепь, содержащую реактивные элементы, например, RC-цепь, то образуется активный фильтр нижних или верхних частот. Наконец, включение в цепь обратной связи ОУ активных компонентов (диодов и транзисторов) позволяет реализовать нелинейные преобразования сигналов с высокой точностью.

Не следует забывать, что усилитель, обычный или операционный, охваченный цепью отрицательной обратной связи, представляет собой пример системы автоматического регулирования (САР), стабилизируемым (регулируемым) параметром которой является коэффициент усиления .

Если усилитель охватить цепью положительной ОС (ПОС), получим, при выполнении определенных условий, генератор колебаний – гармонический или релаксационный.

62