3.5.4 Идеальное интегрирующее звено
Данное звено описывается следующим дифференциальным уравнением:
b1
=aox(t)
(3.38)
Запишем это уравнение в стандартной форме. Для этого разделим (3.38) на b1:
=kx(t),
где
–
коэффициент передачи.
Операторный коэффициент передачи идеального интегрирующего звена
(3.39)
Найдем выражения для переходной функции, используя преобразование Лапласа
Переходя к оригиналу, получим
h(t) = kt1(t) (3.40)
Получим выражение для частотной передаточной функции. Для этого заменим в передаточной функции (3.39) s на j
(
)
Амплитудно-частотная характеристика идеального интегрирующего звена
(3.41)
Фазочастотная характеристика идеального интегрирующего звена
(3.42)
3.5.5 Идеальное дифференцирующее звено
Данное звено описывается следующим уравнением:
(3.43)
Запишем это уравнение в стандартной форме
,
где
- коэффициент передачи.
Запишем
исходное уравнение в операторной форме,
используя формальную подстановку s
=
:
(3.44)
Получим передаточную функцию для идеального дифференцирующего звена. Для этого воспользуемся преобразованием Лапласа:
.
По определению передаточная функция находится как отношение операторного отображения выходного сигнала к операторному отображению входного сигнала. Тогда уравнение (3.44) будет иметь вид:
Y(s) = ksX(s) W(s) = ks (3.45)
Найдем выражения для переходной функции с помощью преобразования Лапласа
Переходя к оригиналу, получим
h(t) = k(t) (3.46)
Перейдем к выражению для частотной передаточной функции.
(
)
Амплитудно-частотная характеристика дифференцирующего звена
(3.47)
Фазо-частотная характеристика идеального дифференцирующего звена
(3.48)
3.5.6 Инерционное дифференцирующее звено
Операторный коэффициент передачи
(3.49)
Найдем выражения для переходной функции
=
Переходя к оригиналу, получим
h(t)
= k
1(t). (3.50)
Найдем выражение для частотной передаточной функции.
(
)
(3.51)
Амплитудно-частотная характеристика инерционного звена
(3.52)
Фазочастотная характеристика инерционного звена
(3.53)
3.5.7 Изодромное звено
Данное звено описывают следующим линейным дифференциальным уравнением:
или
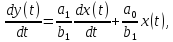
или
(3.54)
где
– коэффициенты передачи.
По определению передаточная функция находится как отношение выходного изображения сигнала к входному изображению. Тогда уравнение (3.53) будет иметь вид:
и
(3.55)
Найдем выражения для переходной функции:
Переходя к оригиналу, получим
h(t)=
1(t).
(3.56)
Перейдем к частотной передаточной функции, заменив в передаточной функции (3.55) s на j:
W(j)=
;
(3.57)
Получим аналитическое выражение для амплитудно-частотной характеристики (АЧХ). По определению амплитудная частотная характеристика - это модуль частотной передаточной функции, т.е.
.
(3.58)
Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.
(3.59)
