3.3 Импульсные характеристики

Дифференциальное уравнение (3.4) является исчерпывающим математическим описанием стационарной линейной САР. В практике инженерного анализа и проектирования САР в качестве типовых задающих воздействий используют единичный скачок и гармоническое колебание, при этом единичный скачок используют для анализа динамики элемента или системы, а с помощью гармонического воздействия оценивают статические характеристики элемента или системы.

Функция Хэвисайда (единичная ступенчатая функция, функция единичного скачка, 1(t)) — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных – рис.3.4.

В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хэвисайда, удобные по тем или иным соображениям, например:

Рис. 3.4 Функция единичного скачка 1(t) (функция Хэвисайда)

Другое распространённое определение:

Реакцию элемента или системы на входную величину в виде функции единичного скачка 1(t) называют переходной характеристикой (переходной функцией) h(t) элемента или системы. Для равенств (3.14) изображение по Лапласу H = H(p) переходной характеристики h(t) определяется выражением

(3.16)

где W = W(s) – передаточная функция элемента или системы; 1/s – изображение по Лапласу функции единичного скачка 1(t).

Функция Хэвисайда является первообразной функцией для дельта-функции Дирака, , это также можно записать как:

или

(3.17)

Иными словами, импульсная функция Дирака относится к классу обобщенных функций и представляет собой производную от функции единичного скачка 1(t).

Импульсная функция Дирака – это импульс с бесконечной амплитудой и бесконечно малой шириной, площадь которого принимают равной 1.

Реакцию элемента или системы на единичную импульсную функцию называютимпульсной характеристикой (функцией веса) . Импульсная характеристика (функция веса) равна производной от переходной характеристики

(3.18)

Для автоматических систем функция веса является менее распространенным видом входного воздействия, чем единичная ступенчатая функция.

3.4 Частотные характеристики

Для оценки установившихся (стационарных) режимов более удобно рассматривать поведение элементов и систем при воздействиях, которые являются периодическими функциями времени.

Гармонические воздействия выбирают вследствие нескольких обстоятельств.

Во-первых, большинство реально встречающихся воздействий может быть представлено в виде суммы гармоник различных частот.

Во-вторых, в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений.

В-третьих, не возникает затруднений в экспериментальном исследовании поведения линейных элементов и систем при гармонических воздействиях.

Пусть на вход стационарного элемента или системы воздействует гармонический сигнал

где – соответственно его амплитуда, частота, начальная фаза и период.

Тогда по истечении определенного промежутка времени на выходе установится гармонический сигнал

той же частоты, но с измененной амплитудой и фазой. Отношение

(3.19)

и разность

(3.20)

называют соответственно амплитудно-частотной и фазочастотной характеристиками рассматриваемого элемента или системы.

Частотные характеристики линейного элемента или системы зависят только от свойств этого элемента или этой системы и не зависят от амплитуды и фазы входных гармонических сигналов.

Частотные характеристики элемента или системы связаны с их передаточными функциями (коэффициентами передачи). Подставив в передаточную функцию W(s) вместо s мнимую частоту jω, получим частотную передаточную функцию .

Несмотря на простую связь между операторной W(s) и комплексной W(jω) функциями передачи между ними имеется принципиальные различия.

W(s) связывает реакцию и воздействие в наиболее общем случае переходных колебаний,

а W(jω) – в частном режиме установившихся гармонических колебаний:

Функция при каждом значении частотыω является комплексной величиной, и поэтому может быть представлена в показательном виде

, (3.21)

где , т.е. модуль и аргумент частотной передаточной функции определяют соответственно амплитудно-частотную и фазочастотную характеристики.

Функция (3.21) также может быть представлена в алгебраическом виде:

(3.22)

где называют соответственно действительной (вещественной) и мнимой частотными характеристиками.

Годограф функции при изменении частоты ω от нуля до бесконечности представляет собой амплитудно-фазовую частотную характеристику (АФЧХ) – рис.3.5.

Рис.3.5

Амплитудно-фазовая частотная характеристика — представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазочастотную характеристики, а это неудобно.

По оси абсцисс откладывают вещественную часть , а по оси ординат – мнимую часть.

На основании равенств (3.21) и (3.22) легко показать связь частотных характеристик между собой:

(3.23)

Вещественная частотная характеристика есть четная функция частоты ω, а мнимая частотная характеристика – нечетная функция:

На западе АФЧХ называют диаграммой Найквиста или годографом Найквиста (англ. Nyquist Plot).

Однако, построение такой характеристики вызывает определенные трудности. Поэтому широко используют асимптотические логарифмические частотные характеристики – амплитудно-частотную (ЛАЧХ или ЛАХ) и фазочастотную (ЛФЧХ или ЛФХ). Их распространение обусловлено как наглядностью представления АЧХ и ФЧХ элемента или системы, так и легкостью построения характеристики в сочетании с удобством анализа устойчивости.

Логарифмическая амплитудно-частотная и фазочастотная характеристики — это представление частотного отклика линейной стационарной системы в логарифмическом масштабе. Ее строят в виде двух графиков: логарифмических амплитудно-частотной характеристики и фазочастотной характеристики, которые обычно располагаются друг под другом. Разбиение АФЧХ или диаграммы Найквиста на два графика резко упрощает ее построение и повышает наглядность описания.

При построении логарифмических АЧХ (ЛАЧХ или ЛАХ) по оси абсцисс откладывают безразмерную частоту в логарифмическом масштабе. Это означает, что частота нормирована к какому-то своему значению, например, к частоте 1Гц, к частоте среза системы ω₀ и т.д. Нуль оси абсцисс лежит слева в бесконечности, поскольку Поэтому ось ординат может пересекать ось абсцисс в любой удобной точке.

По оси ординат ЛАХ откладывают в равномерном масштабе логарифмическую амплитуду 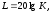т.е. нормированный, например, к единице коэффициент передачи, выраженный в дБ. Нуль логарифмической амплитуды соответствует единичному усилению ().

У логарифмической ФЧХ такая же ось абсцисс "безразмерных" частот, а по оси ординат отложена фаза в градусах или радианах.

Если передаточная функция системы является рациональной, тогда ЛАЧХ может быть аппроксимирована отрезками прямых линий (асимптотами); для построения асимптотических ЛАХ нужны весьма простые вычисления.

Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев системы сложением, что вытекает из свойства логарифма:

.

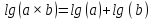Основная идея ЛАЧХ основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции

,

то:

Отметим обратную зависимость между полюсом и нулем. Амплитуда для нуля пропорциональна ω⁺¹, и наклон его графика в логарифмическом масштабе равен +1, а амплитуда для полюса пропорциональна ω ^–1, и наклон его графика равен –1. Аналогично фаза для полюса противоположна по знаку фазе для нуля.

Построить ЛАЧХ можно используя следующие правила:

• на каждой частоте ω, где ω = ω_m (нуль), наклон линии увеличивается на дБ на декаду изменения частоты (0, + 1, + 2,…).

• на каждой частоте ω, где ω = ω_n (полюс), наклон линии уменьшается на дБ на декаду изменения частоты (0, - 1, - 2,…).

В качестве примера рассмотрим пропорционально-дифференцирующиее (ПДФ) и пропорционально-интегрирующее (ПИФ) звенья (фильтры). Их часто применяют в различных САР для коррекции АЧХ – рис.3.6.

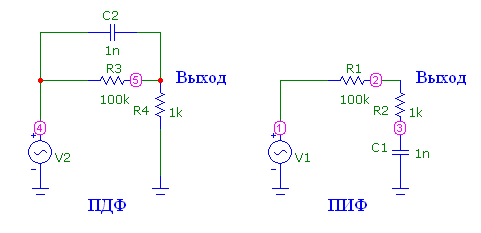
Рис.3.6

Например, для звена пропорционально-дифференцирующего фильтра

,

Ψ = – arctg(ωΤ) + arctg(αωT)

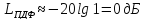где и в области низких частот имеем L_ПДФ 20lg(α). Это низкочастотная асимптота – полубесконечная прямая, лежащая ниже оси абсцисс на 20lg(α) децибел. При начинается новая прямая с наклоном +1. Она продолжается до точкиВ области высоких частот имеем . Это высокочастотная асимптота – полубесконечная прямая с нулевым наклоном. Асимптотическая ЛАХ образуется двумя полубесконечными прямыми и асимптотой с единичным положительным наклоном, которые сопрягаются на частотах излома(рис.3.7 слева). Отметим также, что для звеньев первого порядка значение угла сдвига фазовой характеристика на частотах излома равно – 45º для интегрирующего излома (0 → – 1) и +45º для дифференцирующего излома (0 → + 1).

Для звена пропорционально-интегрирующего фильтра

,

где

Ψ = – arctg(ωΤ₁) + arctg(ωT₂).

В этом случае в области низких частот имеем L_ПИФ 20lg1 = 0. Это низкочастотная асимптота – полубесконечная прямая, лежащая на оси абсцисс. При начинается новая прямая с наклоном –1. Она продолжается до точкиВ области высоких частот имеем . Это высокочастотная асимптота – полубесконечная прямая с нулевым наклоном. Асимптотическая ЛАХ образуется двумя полубесконечными прямыми и асимптотой с единичным отрицательным наклоном, которые сопрягаются на частотах излома(рис.3.7 справа).

Разумеется, аппроксимация гладких кривых (рис.3.8) отрезками прямых и полубесконечных прямых линий есть некоторое приближение. Ошибка аппроксимации максимальна в точке излома и для звеньев первого порядка не превышает 3дБ. При октавной отстройке ошибка уменьшается до 0,97дБ, при отстройке от частоты излома на две октавы ошибка не превысит 0,26дБ и т.д.

Фазовые характеристики аппроксимируют гораздо реже – рис.3.9.

Рис.3.7 Реальные ЛАХ ПДФ и ПИФ

Рис. 3.9 Реальные ЛФХ ПДФ и ПИФ

Заметим также, что особенность ПИФ заключается в том, что, во-первых, его мгновенное выходное напряжение на высоких частотах (ω > ω₂) пропорционально мгновенному значению входного напряжения, а в области частот (ω₁ < ω < ω₂) оно зависит от интеграла последнего. Во-вторых, фазовый сдвиг ПИФ не превышает – 90°, стремясь к нулю вне рабочего интервала ω₁ – ω₂.