Ю.А. Никитин

Курс СТУ. Тема 3

Понятие об обратной связи

Практически ни одна телекоммуникационная система не обходится без цепей обратной связи – и на уровне элементарных узлов, и на уровне устройств, и на уровне подсистем. Обратную связь, в том или ином виде, вводят и для стабилизации параметров (ООС), и для генерации колебаний (ПОС), и для формирования частотных характеристик (фильтрации), и для модуляции – демодуляции при формировании и преобразовании информационных потоков. Поэтому знание основ теории САР является одним из важных моментов в подготовке современных специалистов телекоммуникаций.

Заметим, что двухкаскадный усилитель можно охватить как минимум тремя обратными связями, трехкаскадный – пятью ООС и т.д. – рис.3.1.

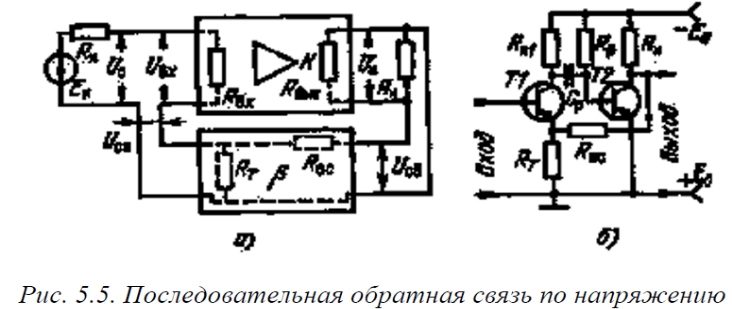
3.1 Математическое описание элементов

На практике широко используют представление элементов САР в виде их передаточных функции, которые являются специфической записью линейных дифференциальных уравнений и позволяют давать математическое описание систем в виде наглядных структурных схем. Понятие о передаточных функциях и их определение основывается на преобразовании Лапласа.

Временные и частотные характеристики, с помощью которых описывают поведение элементов и систем в переходных и установившихся режимах, используют и при анализе, и при синтезе САР. Эти характеристики не учитывают физическую природу объектов, а обращают внимание только на их динамические свойства. Другими словами, в теории САР рассматривают математические модели элементов структуры – динамические звенья.

Передаточные функции, структурные схемы, временные и частотные характеристики, а также типовые динамические звенья составляют основу того математического аппарата, который используют в теории автоматического регулирования.

В основе всех перечисленных понятий лежит описание динамических свойств элементов и систем дифференциальными уравнениями. Однако, эти понятия и этот математический аппарат позволяют проводить анализ и синтез САР без интегрирования дифференциальных уравнений и непосредственного исследования их решений.

Переходный процесс системы можно определить при помощи дифференциальных уравнений отдельных ее элементов или всей системы. В общем случае такое уравнение нелинейно. Для аналитического решения задачи в общем виде целесообразно заменить нелинейное дифференциальное уравнение линейным. Такую операцию называют линеаризацией.

Основой линеаризации уравнений является выдвинутое И. А. Вышнеградским предположение, что в течение всего процесса регулирования имеют место достаточно малые отклонения всех изменяющихся переменных от их установившихся значений. Вводя в нелинейные уравнения процесса управления не абсолютные значения переменных, а их отклонения, можно перейти к линейным уравнениям в приращениях.

Линеаризация уравнений и их запись в приращениях позволяют получить нулевые начальные условия. Почему – потому, что в окрестностях точки устойчивого равновесия.

В общем случае для приведения уравнений к форме в конечных приращениях используют формулу разложения аналитической функции в ряд Тейлора; также считают, что движение происходит в пределах малых отклонений от установившегося состояния, а производные имеют единственное и конечное значение, отличное от нуля.

Для непрерывной функции Y = f(x), имеющей n непрерывных производных в окрестностях точки устойчивого равновесия

,

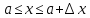формула Тейлора имеет вид:

(3.1)

Членами ряда второго и выше порядка малости обычно пренебрегают. Далее вычитают значения функции для установившегося состояния и вместо (3.1) получают

(3.2)

где – производная функции по входной переменной, которую определяют, как тангенс угла наклона α статической характеристики элемента в заданной точке (A, X₀) – рис.3.2.

Формула (3.2) представляет собой уравнение в приращениях; ее можно применять к линейным и нелинейным аналитическим функциям.

Линеаризация нелинейной функции методом малых отклонений означает замену кривой в точке устойчивого равновесия касательной к этой кривой.

При записи линейного дифференциального уравнения искомую функцию времени и ее производные принято записывать в левой части, а входные величины (заданные функции времени) в правой. При записи уравнения обычно используют оператор дифференцирования p или , который формально считают алгебраической величиной. При этом, ….

Для примера, запишем линейное дифференциальное уравнение второго порядка следующим образом

(3.3)

,

где

– линейные дифференциальные операторы.

Если к однокоординатной САР приложено задающее воздействие g = g(t) и возмущение (помеха) f = f(t), то ее уравнение в общем случае можно записать в виде:

, (3.4)

где

– линейные дифференциальные операторы с постоянными коэффициентами, причем

Для линейного дифференциального уравнения с постоянными коэффициентами выполняется чрезвычайно важный принцип суперпозиции. Он заключается в том, что каждая входная величина (заданная функция времени) создает составляющую выходной величины (искомой функции времени) независимо

- от наличия и характера изменения других входных величин;

- от начальных условий.

При этом начальные условия вызывают переходный процесс, который не зависит от входных величин.

Начальными условиями уравнения n-го порядка называют значения выходной величины (искомой функции времени) и ее производных до (n - 1) включительно в начальный момент времени.

Принцип суперпозиции, следовательно, означает, что решение y = y(t) уравнения (3.4) равно сумме трех составляющих

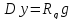где есть решения неоднородных уравненийипри нулевых начальных условиях, аесть решение однородного уравнения

(3.5)

при заданных начальных условиях. Последнюю составляющую называют свободной составляющей и определяют значениями корней характеристического уравнения

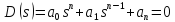, (3.6)

где s – комплексная величина.

Общее решение однородного уравнения (3.5) представляет собой сумму частных решений, которые зависят от корней характеристического уравнения (3.6):

каждому вещественному корню соответствует частное решение вида

; (3.7)

каждому вещественному корню кратности ν соответствует ν частных решений

…+; (3.8)

каждой паре сопряженных комплексных корней исоответствуют два частных решения

(3.9)

каждой паре сопряженных комплексных корней икратности μ соответствует 2μ частных решений

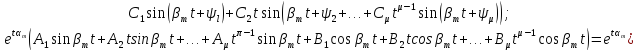(3.10)

При инженерных расчетах линейные дифференциальные уравнения удобнее всего решать операторным методом.