
Представление знаний в информационных системах Птицына 56 / Laboratornaya_5_Deyko
.docx
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования "Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича"
Отчёт
по лабораторной работе №5 по теме: «Анализ и генерация знаний на основе методов преобразования функциональных моделей (одноуровневое управление потоков заданий в серверной системе)»
Дисциплина: Представление знаний в информационных системах
Выполнил: студент группы ИСТ-01 Дейко К. Г.
Проверила: проф. д.т.н. Птицына Л.К.
Санкт-Петербург
2012
Задание
-
Извлечь знания об одноуровневом управлении потоками в серверной системе. Для извлечения использовать электронную версию исходных материалов.
-
Построить концептуальную модель одноуровневого управления потоками заданий в серверной системе.
-
Выделить математическое ядро определения показателей качества одноуровневого управления потоком заданий в серверной системе.
-
Разработать приложение для определения показателей качества одноуровневого управления потоком заданий в серверной системе. Приложение должно быть написано на любом языке либо с использованием любого математического пакета (Mathcad, Matlab, Scilab и т.д.)
-
Подтвердить работоспособность созданного приложения. Для подтверждения использовать оценки показателей качества управления, представленные в исходном материале.
-
Подтвердить выполняемость условий об эквивалентном качестве одноуровневого управления потоков заданий в серверной системе.
Ход работы
-
Извлечение знаний об одноуровневом управлении потоками в серверной системе из исходного материала.
-
Построение концептуальной модели одноуровневого управления потоками заданий в серверной системе.
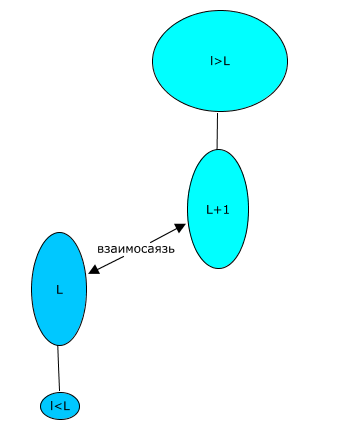
Приложение, определяющее показатели качества одноуровневого управления потоком заданий в серверной системе
Для расчета и сравнительного анализа динамических характеристик систем защиты управления, использующих метод одноуровневого управления используем рассмотренные ранее соотношения (1)-(14). Параметры исследуемых систем заданы в таблице 1.
Таблица 1
Параметры исследуемых систем
|
|
System #1 |
System #2 |
|
|
|
|
|
|
|
|
|
Механизм управления |
Одноуровневое |
Одноуровневое |
|
Параметры управления |
|
|
где
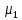
![]() — интенсивность потока ответов сервера
для режима работы с первым сервером;
— интенсивность потока ответов сервера
для режима работы с первым сервером;

![]() — интенсивность потока ответов сервера
для режима работы со вторым сервером;
— интенсивность потока ответов сервера
для режима работы со вторым сервером;
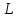
![]() — интенсивность входящего потока
запросов, при которой выполняется
переключение режима работы при
одноуровневом управлении;
— интенсивность входящего потока
запросов, при которой выполняется
переключение режима работы при
одноуровневом управлении;
Параметры 
![]() и
и 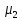
![]() для исследуемых систем отличаются между
собой на порядок, что отражает увеличение
интенсивности потока ответов.
для исследуемых систем отличаются между
собой на порядок, что отражает увеличение
интенсивности потока ответов.
Интенсивность
поступления запросов 
![]() - изменяемый параметр.
- изменяемый параметр.
Для оценки динамических характеристик реализуем необходимые функции в среде Matlab.
Функция fun_N(lam,
m_1,
m_2,
L)
вычисляет
значение 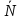
![]() – среднее количество запросов, находящихся
в системе, при одноуровневом управлении:
– среднее количество запросов, находящихся
в системе, при одноуровневом управлении:
function N = fun_N(lam, m_1, m_2, L)
r_1=lam./m_1;
r_2=lam./m_2;
P_0=((1-r_1).*(1-r_2))./(1-r_2-r_1.^L.*(r_1-r_2));
N=(P_0).*(r_1./(1-r_1).^2-((r_1.^L.*(r_1-r_2))./((1-r_1).*(1-r_2))).*(L+(1-r_1.*r_2)./((1-r_1).*(1-r_2))));
end
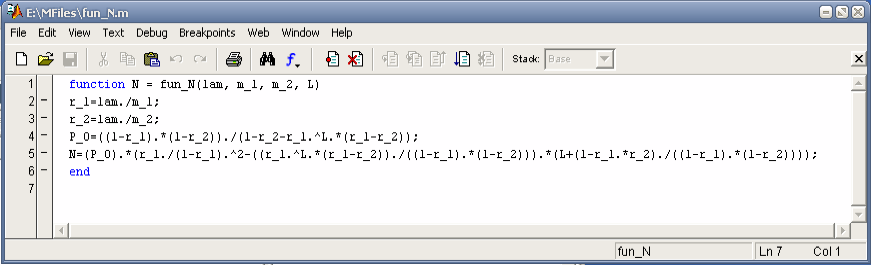
Функция fun_Q(lam,
m_1,
m_2,
L)
вычисляет
значение 
![]() – среднее количество запросов, ожидающих
обработки, при одноуровневом управлении:
– среднее количество запросов, ожидающих
обработки, при одноуровневом управлении:
function Q = fun_Q(lam, m_1, m_2, L)
r_1=lam./m_1;
r_2=lam./m_2;
P_0=((1-r_1).*(1-r_2))./(1-r_2-r_1.^L.*(r_1-r_2));
Q=P_0 + P_0.*((r_1.^L.*r_2)./(r_2 - 1).^2 - (r_1.*(r_1.^L - 1))./(r_1 - 1).^2 + (L.*r_1.*r_1.^(L - 1))./(r_1 - 1) - (L.*r_1.*r_1.^(L - 1))./(r_2 - 1)) - P_0.*((r_1.^L - 1)./(r_1 - 1) - r_1.^L./(r_2 - 1));
end
Построим графики зависимостей N и Q от входной интенсивности.

Графики зависимостей

![]() и
и 
![]() для исследуемых систем с одноуровневым
управлением
для исследуемых систем с одноуровневым
управлением
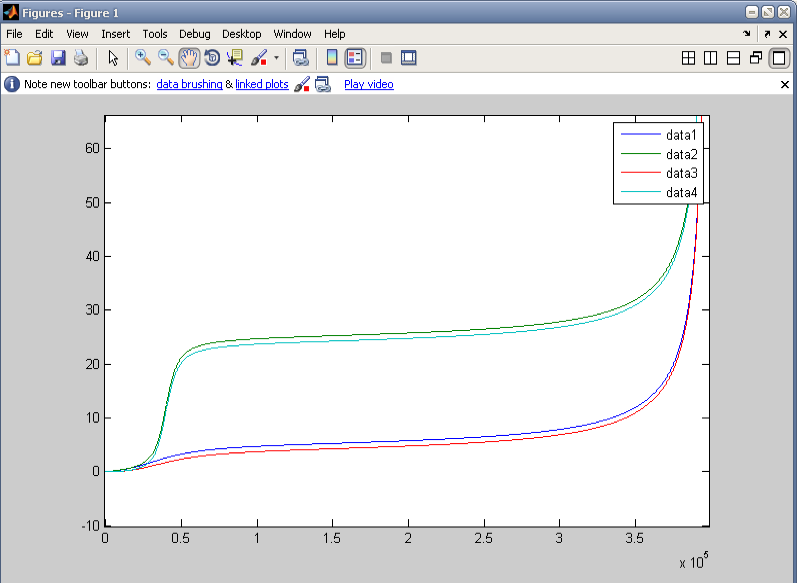
Величины 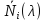
![]() и
и 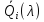
![]() – характеристики для i-й
системы. Из графиков видно, что
характеристики
– характеристики для i-й
системы. Из графиков видно, что
характеристики 
![]() и
и 
![]() монотонно возрастают с увеличением
интенсивности входящего потока
монотонно возрастают с увеличением
интенсивности входящего потока 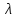
![]() .
.
При 
![]() длина очереди не превышает порогового
значения L
для систем с одноуровневым управлением,
так как система работает преимущественно
с первым сервером. При приближении
величины
длина очереди не превышает порогового
значения L
для систем с одноуровневым управлением,
так как система работает преимущественно
с первым сервером. При приближении
величины 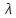
![]() к значению
к значению 
![]() система работает преимущественно со
вторым сервером; длина очереди на
некотором интервале возрастает слабо,
затем неограниченно возрастает. При
система работает преимущественно со
вторым сервером; длина очереди на
некотором интервале возрастает слабо,
затем неограниченно возрастает. При
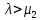
![]() система уже не в состоянии обработать
входящий поток запросов, характеристики
система уже не в состоянии обработать
входящий поток запросов, характеристики
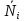
![]() и
и 
![]() определить нельзя.
определить нельзя.
Из графиков видно, что выполняются соотношения для характеристик
N1<=N2 и Q1<=Q2.
Далее, построим графики зависимостей среднего времени простаивания в очереди от интенсивности входящего потока запросов.
function W=fun_W(lam,m_1,m_2,L)
r_1=lam./m_1;
r_2=lam./m_2;
P_0=((1-r_1).*(1-r_2))./(1-r_2-r_1.^L.*(r_1-r_2));
W=(P_0./lam).*(1+(2.*r_1-1)./(r_1-1).^2+r_1.^L.*(r_2./(r_2-1).^2-r_1./(r_1-1).^2+(L-1).*(r_2-r_1)./(r_1-1)./(r_2-1)));
end
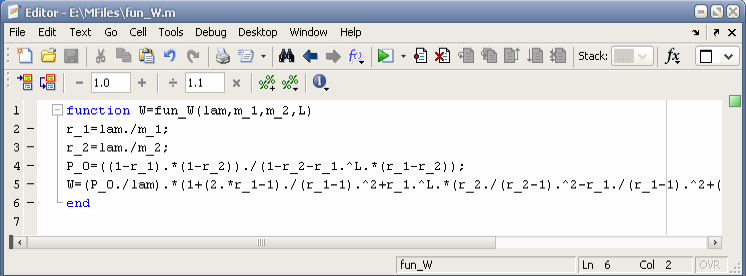

Графики зависимостей
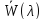
![]() для исследуемых систем.
для исследуемых систем.
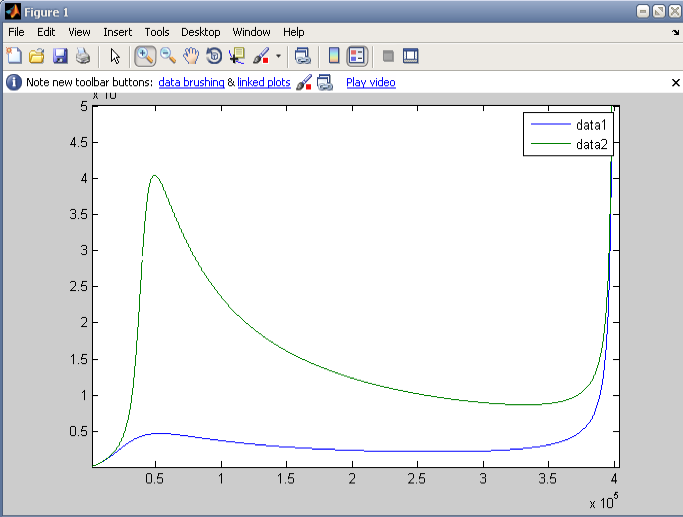
Величина 
![]() – среднее время простаивания в очереди
для i-й
системы. Из графиков видно, что значение
– среднее время простаивания в очереди
для i-й
системы. Из графиков видно, что значение

![]() монотонно возрастает с увеличением
интенсивности входящего потока
монотонно возрастает с увеличением
интенсивности входящего потока 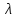
![]() при
при 
![]() ;
при
;
при 
![]() близком к
близком к 
![]() функция
функция 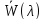
![]() имеет локальный максимум. При приближении
величины
имеет локальный максимум. При приближении
величины 
![]() к значению
к значению 
![]() на некотором интервале среднее время
простаивания в очереди убывает, так как
возрастает вероятность нахождения
системы в режиме работы со вторым
сервером. При
на некотором интервале среднее время
простаивания в очереди убывает, так как
возрастает вероятность нахождения
системы в режиме работы со вторым
сервером. При 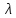
![]() близком к
близком к 
![]() функция
функция 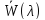
![]() неограниченно возрастает. При
неограниченно возрастает. При 
![]() система уже не в состоянии обработать
входящий поток запросов, и характеристику
система уже не в состоянии обработать
входящий поток запросов, и характеристику

![]() определить нельзя. Также из графиков
видно, что выполняется соотношение
определить нельзя. Также из графиков
видно, что выполняется соотношение
W1<=W2
function S = fun_S(lam, m_1, m_2, L)
r_1=lam./m_1;
r_2=lam./m_2;
P_0=((1-r_1).*(1-r_2))./(1-r_2-r_1.^L.*(r_1-r_2));
S=(P_0./lam).*(r_1./(1-r_1).^2-r_1.^2./(1-r_1).^2-r_1.^L.*(r_1-r_2)./(1-r_1)./(1-r_2).*(L+(1-r_1.*r_2)./(1-r_1)./(1-r_2))-r_1.^L.*(r_2./(1-r_2).^2-r_1./(1-r_1).^2+(L-1).*(r_2-r_1)./(1-r_1)./(1-r_2)));
end

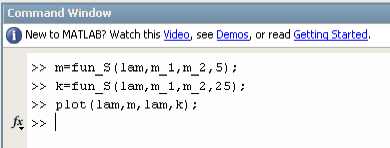
Графики
зависимостей 
![]() для исследуемых систем.
для исследуемых систем.
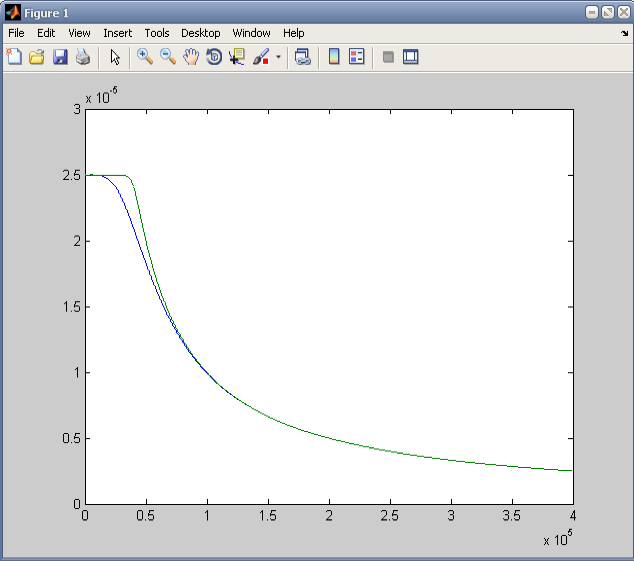
Величина 
![]() – среднее время обслуживания для i-й
системы. Из графика видно, что при
– среднее время обслуживания для i-й
системы. Из графика видно, что при 
![]() на некотором интервале среднее время
обслуживания не изменяется и равно
приблизительно
на некотором интервале среднее время
обслуживания не изменяется и равно
приблизительно 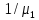
![]() ,
так как система работает преимущественно
в режиме с первым сервером. При приближении
величины
,
так как система работает преимущественно
в режиме с первым сервером. При приближении
величины 
![]() к значению
к значению 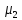
![]() среднее время обслуживания монотонно
убывает и стремится к величине
среднее время обслуживания монотонно
убывает и стремится к величине 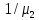
![]() ,
так как увеличивается вероятность
нахождения системы в режиме работы со
вторым сервером. Также из графиков
видно, что выполняется соотношение
,
так как увеличивается вероятность
нахождения системы в режиме работы со
вторым сервером. Также из графиков
видно, что выполняется соотношение
S1<S2
Вычислим
характеристики работы систем, параметры
которых определены в таблице 1, для двух
заданных значений интенсивности
входящего потока запросов к серверу

![]() .
Результаты вычислений представлены в
таблице 2.
.
Результаты вычислений представлены в
таблице 2.
Таблица 2
Характеристики работы системы при различной интенсивности входящего потока
|
|
|
|
|
|
System #1 |
|
2.358 |
|
|
|
|
|
|
|
|
|
|
|
|
System #2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице 2 величины
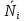
![]() ,
,

![]() ,
,
![]() – характеристики i-й
системы: среднее количество запросов
в системе, среднее время простаивания
в очереди, среднее время обслуживания,
соответственно.
– характеристики i-й
системы: среднее количество запросов
в системе, среднее время простаивания
в очереди, среднее время обслуживания,
соответственно.
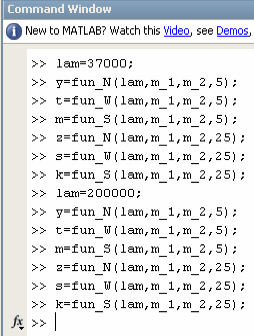
>> lam=37000;
>> y=fun_N(lam,m_1,m_2,5);
>> t=fun_W(lam,m_1,m_2,5);
>> m=fun_S(lam,m_1,m_2,5);
>> z=fun_N(lam,m_1,m_2,25);
>> s=fun_W(lam,m_1,m_2,25);
>> k=fun_S(lam,m_1,m_2,25);

>> lam=200000;
>> y=fun_N(lam,m_1,m_2,5);
>> t=fun_W(lam,m_1,m_2,5);
>> m=fun_S(lam,m_1,m_2,5);
>> z=fun_N(lam,m_1,m_2,25);
>> s=fun_W(lam,m_1,m_2,25);
>> k=fun_S(lam,m_1,m_2,25) ;
Реализуем функции, позволяющие построить графики дискретного распределения случайной величины N.
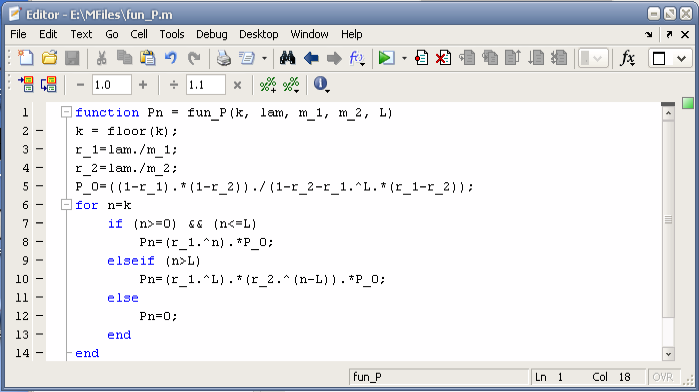
Функция fun_P(k, lam, m_1, m_2, L) вычисляет вероятность нахождения системы в состоянии k при одноуровневом управлении.
function Pn = fun_P(k, lam, m_1, m_2, L)
k = floor(k);
r_1=lam./m_1;
r_2=lam./m_2;
P_0=((1-r_1).*(1-r_2))./(1-r_2-r_1.^L.*(r_1-r_2));
for n=k
if (n>=0) && (n<=L)
Pn=(r_1.^n).*P_0;
elseif (n>L)
Pn=(r_1.^L).*(r_2.^(n-L)).*P_0;
else
Pn=0;
end
end
end
Функция gisterP(k, lam, m_1, m_2, L_1, L_2) вычисляет вероятность нахождения системы в состоянии k при гистерезисном управлении.
function Pn = gister_P(k, lam, m_1, m_2, L_1, L_2)
k = floor(k);
r=lam./m_1;
r_1=lam./m_2;
q=L_2-L_1-1;
P_0=(1./(1-r)-((q+1).*r.^(L_1+q).*(r-r_1))./((1-r.^(q+1)).*(1-r_1))).^(-1);
for n=k
if (n>=0) && (n<=L_1)
Pn=(r.^n).*P_0;
elseif (n>L_1) && (n<L_2)
Pn=(r.^(L_1).*(1-r))./(1-r.^(q+1)).*P_0.*((r.^(n-L_1)-r.^(q+1))./(1-r)+(r.^q.*r_1.*(1-r_1.^(n-L_1)))./(1-r_1));
elseif (n>=L_2)
Pn=((1-r_1.^(q+1)).*(1-r).*r.^(L_1+q))./((1-r.^(q+1) ).*(1-r_1)).*r_1.^(n-L_1-q).*P_0;
else
Pn=0;
end
end
end

Также построим
для заданных значений интенсивности
входящего потока графики распределения
случайной величины N
(количества находящихся в системе
запросов) и проверим соответствие
распределений полученным выше значениям

![]()
>> for i=1:40
rez1(i)=fun_P(i,37000,m_1,m_2,5);
rez2(i)=fun_P(i,37000,m_1,m_2,25);
rez3(i)=gister_P(i,37000,m_1,m_2,5,25);
end
>> rezx=1:40;
>> plot(rezx,rez1,rezx,rez2,rezx,rez3);

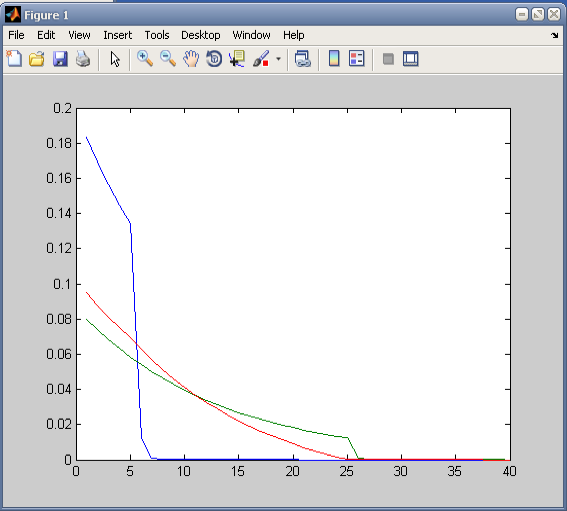
Величина 
![]() – стационарная вероятность нахождения
i-й
системы в состоянии n
при заданной интенсивности входящего
потока.
– стационарная вероятность нахождения
i-й
системы в состоянии n
при заданной интенсивности входящего
потока.
|
|
|
Из графиков видно,
что при 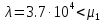
![]() вероятность нахождения системы в режиме
работы первым сервером для всех
исследуемых систем выше вероятности
нахождения системы в режиме работы со
вторым сервером. Это объясняется тем,
что при данном значении
вероятность нахождения системы в режиме
работы первым сервером для всех
исследуемых систем выше вероятности
нахождения системы в режиме работы со
вторым сервером. Это объясняется тем,
что при данном значении 
![]() переход в режим работы с кешированием
приводит к быстрому уменьшению длины
очереди и возвращению в режим работы
без кеширования. При
переход в режим работы с кешированием
приводит к быстрому уменьшению длины
очереди и возвращению в режим работы
без кеширования. При 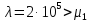
![]() функции распределения для систем с
одноуровневым управлением имеют ярко
выраженный максимум вблизи значений
n,
равных заданным для систем параметрам
L.
Функции распределения для системы с
гистерезисным управлением не имеет
ярко выраженного максимума, т.е. дисперсия
величины N
значительно выше.
функции распределения для систем с
одноуровневым управлением имеют ярко
выраженный максимум вблизи значений
n,
равных заданным для систем параметрам
L.
Функции распределения для системы с
гистерезисным управлением не имеет
ярко выраженного максимума, т.е. дисперсия
величины N
значительно выше.
Характер графиков
распределения при 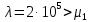
![]() позволяет сделать следующий вывод:
система с одноуровневым управлением
при высокой интенсивности входящего
потока будет большую часть времени
находиться в состоянии, при котором
длина очереди N
близка к значению L.
Это означает, что в системе будет
происходить частое переключение из
одного режима работы в другой, которое
может негативно сказаться на динамических
характеристиках системы при наличии
временных затрат на переключение.
Система с гистерезисным управлением
лишена указанного недостатка, поскольку
переключение между режимами работы
происходит при различных значениях N.
позволяет сделать следующий вывод:
система с одноуровневым управлением
при высокой интенсивности входящего
потока будет большую часть времени
находиться в состоянии, при котором
длина очереди N
близка к значению L.
Это означает, что в системе будет
происходить частое переключение из
одного режима работы в другой, которое
может негативно сказаться на динамических
характеристиках системы при наличии
временных затрат на переключение.
Система с гистерезисным управлением
лишена указанного недостатка, поскольку
переключение между режимами работы
происходит при различных значениях N.
Анализ графиков
показывает, что значения средней длины
очереди 
![]() ,
вычисленные и приведенные в таблице 2,
соответствуют распределениям вероятностей
длины очереди N.
,
вычисленные и приведенные в таблице 2,
соответствуют распределениям вероятностей
длины очереди N.
Подтверждение работоспособности созданного приложения
Выполним
проверку выполнения условия 
![]() .
.
Проверка для системы с одноуровневым управлением:
>> sum1=0;
>> for i=0:500
sum1=sum1+fun_P(i,lam,m_1,m_2,5);
end
>> sum1
sum1 =
1

Результат подтверждает выполнение условия равенства суммы стационарных вероятностей единице.


|
|
|
|
|
|
System #1 |
|
2.358 |
|
|
|
|
|
|
|
|
|
|
|
|
System #2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сопоставлены полученные оценки показателей качества с прототипом. При одинаковых исходных данных оценки совпадают, следовательно, созданное приложение работоспособно.
Вывод.
Выполнен анализ и генерация знаний на основе методов преобразования функциональных моделей одноуровневого управления потоком заданий в серверной системе. Разработаны концептуальные модели одноуровневого управления потоком заданий в серверной системе в инструментальной среде CmapTools.
Разработаны альтернативные приложения, определяющие оценку показателей качества одноуровневого управления потоком заданий в серверной системе. Приложения созданы в среде Matlab. Подтверждена работоспособность созданных приложений посредством сопоставления полученных оценок показателей качества с прототипом. При одинаковых исходных данных оценки совпадают. Проверено условие эквивалентности одноуровневого управления. Для проверки использованы результаты разработанного приложения и прототипа. Получены новые знания об одноуровневом управлении потоком заданий в серверной системе.
