ДТО Занятие 43

Математика 1 курс СПб ГУТ Колледж телекоммуникаций

ДТО Занятие № 43 Параллельность плоскостей 4

Занятие № 43 ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

1. Параллельные плоскости.

2. Признак параллельности двух плоскостей.

3. Свойства параллельных плоскостей.

4. Решение задач.

1. Параллельные плоскости.

Определение. Две плоскости называются параллельными, если они не пересекаются.

На рисунке изображены параллельные плоскости.

Взаимное расположение двух плоскостей в пространстве: две плоскости в пространстве либо имеют общие точки, т.е. пересекаются, либо не имеют общих точек, т.е. параллельны.

2. Признак параллельности двух плоскостей.

Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

3. Свойства параллельных плоскостей.

Свойство 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Если α∥β и они пересекаются с γ, то а∥

Свойство 2. Отрезки параллельных прямых, заключённые между параллельными плоскостями равны.

Если α∥β и AB∥CD, то АВ = CD.

Свойство 3. Если прямая пересекает плоскость, то она пересекает также любую плоскость параллельную данной.

Свойство 4. Если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую.

Свойство 5. Через точку не лежащую в данной плоскости проходит плоскость параллельная данной и притом только одна.

Свойство 6. Если две плоскости параллельны третьей, то они параллельны между собой.

4. Решение задач.

Задача:

Три отрезка , и , не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости и параллельны.

Решение.

Пусть O – точка пересечения отрезков 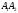, и . Рассмотрим четырёхугольник 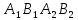. В этом прямоугольнике диагонали и точкой пересечения делятся пополам, а значит прямоугольник – параллелограмм. Тогда стороны и параллельны.

Аналогично доказывается параллельность и .

В итоге получаем, что две пересекающиеся прямые и параллельны двум пересекающимся прямым и , значит по признаку параллельности двух плоскостей плоскости и параллельны.

Контрольные вопросы и задания:

:

1. Точка B не лежит в плоскости треугольника ADC, точки M, N, и P – середины отрезков BA, BC и BD соответственно.

• Докажите, что плоскости MNP и ADC параллельны.

• Найдите площадь треугольника MNP, если площадь треугольника ADC равна 48.

2. Параллельные отрезки , и 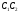заключены между параллельными плоскостями и .

• Определите вид четырёхугольников , и .

• Докажите, что .

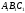3. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках , и , а другую – в точках , и . Докажите, что треугольники и 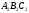подобны.