ДТО Занятие 41

Математика 1 курс СПб ГУТ Колледж телекоммуникаций

ДТО Занятие № 41 Параллельность прямых, прямой и плоскости 5

Занятие №41 ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ

1. Параллельные прямые в пространстве.

2. Параллельность трёх прямых. Параллельность прямой и плоскости.

3. Решение задач.

1. Параллельные прямые в пространстве.

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Пример. На рисунке прямыеa и b параллельны.

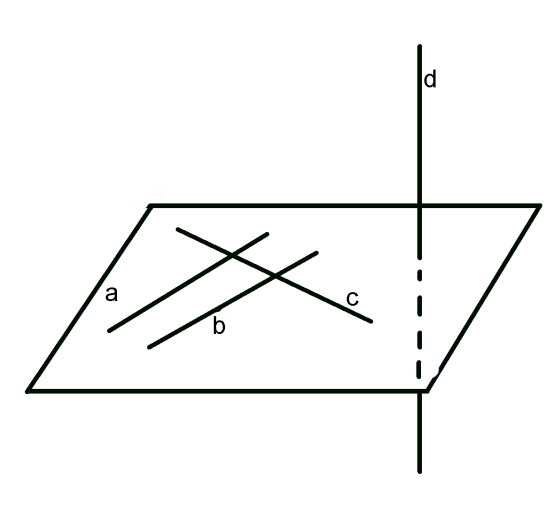
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

Пример. На рисунке отрезки ABи DC параллельны.

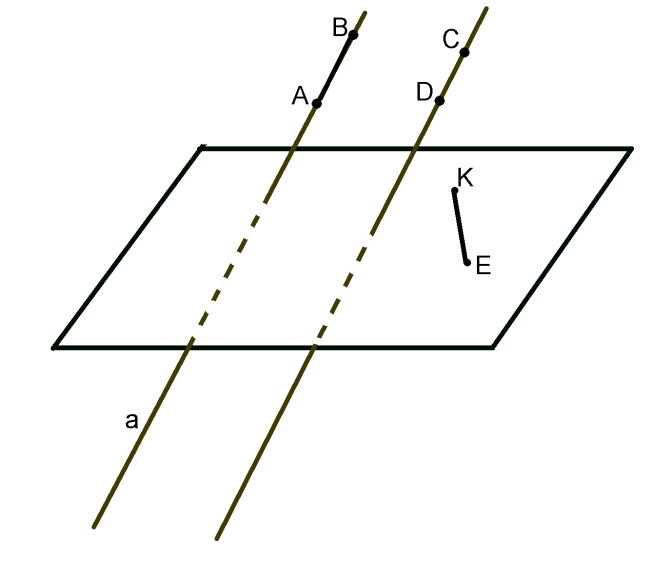
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

2. Параллельность трёх прямых. Параллельность прямой и плоскости.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Случаи взаимного расположения прямой и плоскости в пространстве:

1. Прямая лежит в плоскости;

2. Прямая и плоскости имеют только одну общую точку, т.е. пересекаются;

3. Прямая и плоскость не имеют ни одной общей точки.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

3. Решение задач.

1. Задача №1.

Точка C лежит на отрезке AB. Через точку A проведена плоскость, а через точки Bи C– параллельные прямые, пересекающие эту плоскость, соответственно в точках и . Найдите длину отрезка C, если и B=20см.

Решение.

1. Пусть α – плоскость, проходящая через точку A, а точки и - лежат в плоскости α.

2. Так прямые и параллельные прямые, то они определяют плоскость β, которая пересекает плоскость α по прямой.

3. ПрямыеAB и пересечены двумя параллельными прямыми, значит по теореме Фалеса AC:CB=:.

4. Рассмотрим треугольники и . Эти треугольники подобны

(по углу и двум подобным сторонам) с коэффициентом подобия . Тогда , значит и (см).

Ответ: 12см.

2. Задача №2.

На рисунке точки M, N, Pи Q – середины отрезков DB, DC, ACи AB. Найдите периметр четырёхугольника MNPQ, если AD=12см, BC=14см.

Решение.

1. Рассмотрим треугольник BDC. Точка M середина DBи N – середина DC, значит MN–средняя линия треугольника BDC, тогда 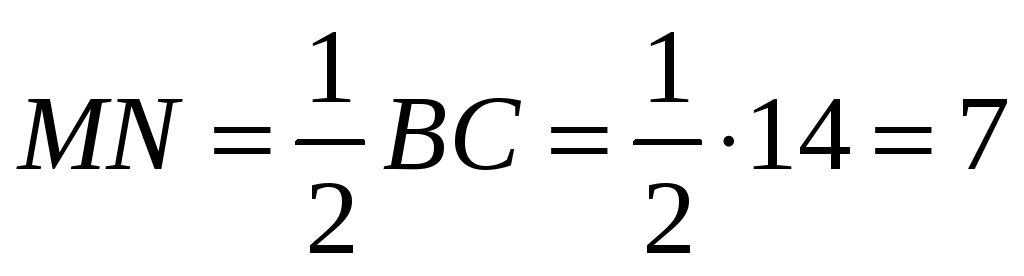(см) и .

2. Рассмотрим треугольник ABC. Точка Q – середина AB и P – середина AC, значит QP – средняя линия ABC, тогда и .

3. Так как и , то . Так как и , то . Итак, получили, что и 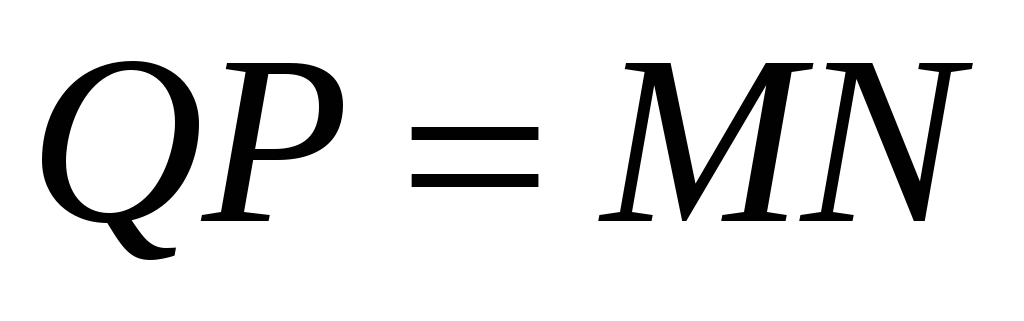, из чего следует, что MNPQ – параллелограмм.

4. Рассмотрим треугольник ABD. Точка Q – середина AB и точка M – середина DB, значит QM – средняя линия ABD, тогда (см).

5. Так как MNPQ – параллелограмм, то его периметр равен 2QM+2MN=12+14=26(см).

Ответ: 26 см.

Контрольные вопросы и задания:

1. Точка C лежит на отрезке AB. Через точку A проведена плоскость, а через точки Bи C– параллельные прямые, пересекающие эту плоскость, соответственно в точках и . Найдите длину отрезка C, если точка C – середина отрезка AB и B=7см.

2. Дан треугольник ABC. Плоскость, параллельная прямой AB, пересекает сторону AC этого треугольника в точке , а сторону BC – в точке . Найдите длину отрезка , если AB=15см, .