20 вариант

Министерство образования Российской Федерации

–––––––––––––––––

Санкт-Петербургская Государственная лесотехническая академия

имени С. М. Кирова

Кафедра технологии деревообрабатывающих производств

Курс: «Основы научных исследований»

Курсовая работа

на тему:

«Исследование процесса деревообработки методом полного факторного эксперимента»

МТ.ДБ.44.308100.КП20

Выполнил: студентка __________________________ О. В. Михеева

Проверил: преподаватель _______________________Е.Г. Кузнецова

Санкт-Петербург

2012

Содержание.

1. Введение …………………………………………………………………………………….3

2. Исходные данные для проведения исследования ………………………………………..4

3. Исследование свойства древесностружечных плит ……………………………………...5

4. Заключение ………………………………………………………………............................11

5. Список использованной литературы ……………………………………………………..12

Введение.

При проведении научных исследований в области дерево­обработки широко используют методы однофакторного и мно­гофакторного экспериментов. По методу однофакторного экс­перимента последовательно изучается влияние на процесс каждого из принятых переменными факторов. Методика мно­гофакторного эксперимента позволяет изучать процесс при изменении в каждом последующем опыте одновременно не­скольких переменных факторов. Достоинствами метода мно­гофакторного эксперимента в сравнении с однофакторным являются: значительное сокращение числа опытов для реше­ния задач исследования, возможность построения по резуль­татам исследования уравнения регрессии — математико-статистической модели изучаемого процесса, позволяющей ис­следовать, оптимизировать процесс и управлять им. При этом процесс исследуется и управляется в условиях воздействия на него факторов в их взаимосвязи.

Одним из таких методов является метод полного фактор­ного эксперимента (ПФЭ), который применяется на первом этапе исследования процессов. С его помощью удается при небольших затратах времени и средств получить информа­цию об изучаемом процессе, хотя и не всегда полную.

Целью выполнения курсовой работы на тему: «Исследо­вание процесса деревообработки методом полного факторного эксперимента» является овладение методикой планирования ПФЭ, обработки и анализа его результатов.

1.Исходные данные для проведения исследования.

Номер варианта	Две последние цифры шифра	Номер исходной зависимости (рисунка)	Обозначение факторов	Интервал варьирования факторов
				НУ	ВУ
1	2	3	4	5
20	40	2.10	X1	25 с	35 с
			X2	100 г/м2	110 г/м2

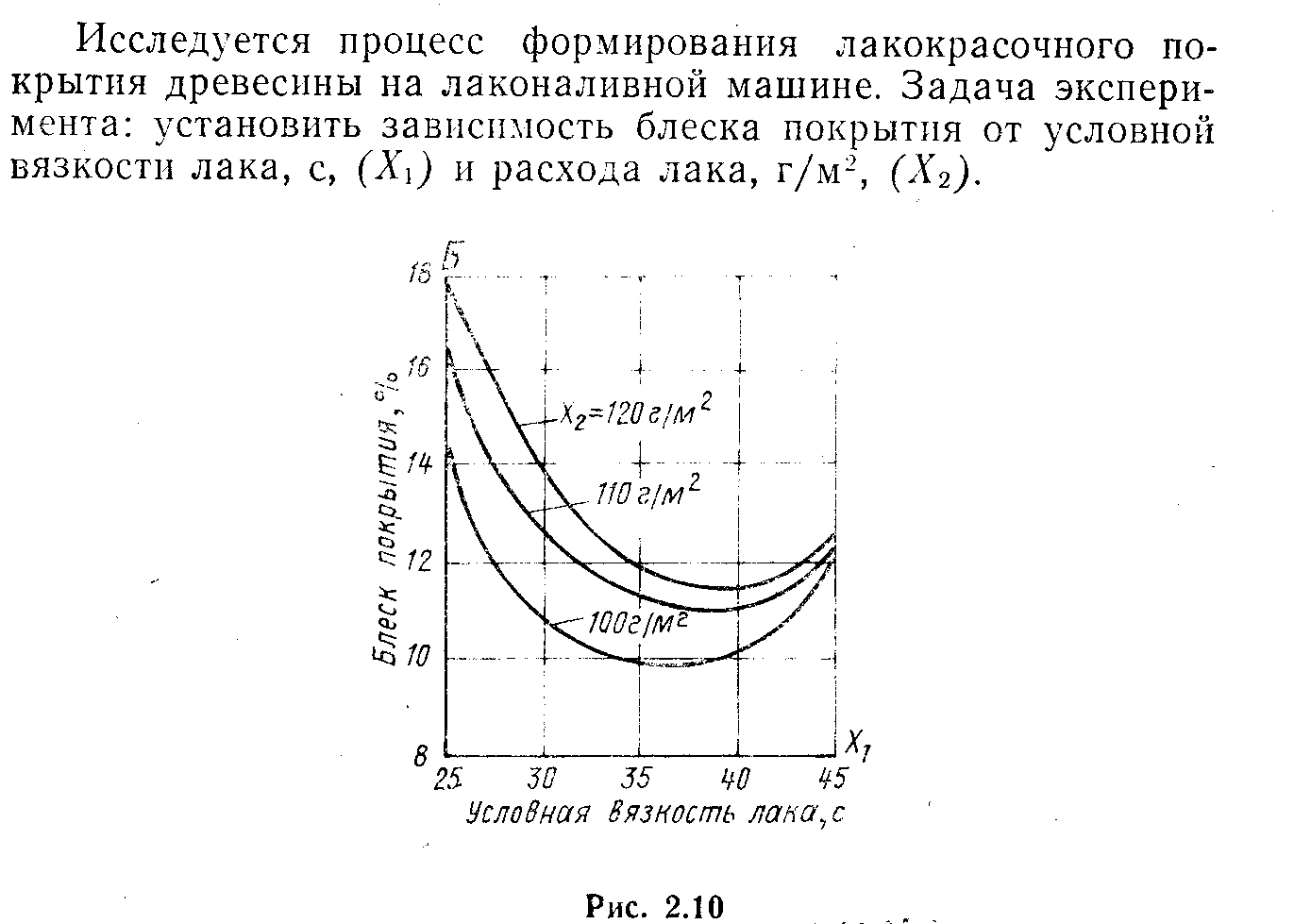
2. Исследование свойства древесностружечных плит.

2.1. Определение основных уровней факторов и интервалов варьирования.

Нижний уровень: для X_1min=25 с, для X_2min= 100 г/м²

Верхний уровень: для X_1max= 35 с, для X_2max=110 г/м².

Основные уровни факторов Х_i^о определяются по формуле:

X_i⁰= (X_imin+X_imax)/2,

где X_imin, X_imax - значения i-ого фактора на нижнем и верхнем уровнях в натуральном виде.

Для первого фактора основной уровень равен:

X₁⁰= (25+35)/2=30

а для второго фактора:

X₂⁰= (100+110)/2=105

Интервалы варьирования определяются по формуле:

I_i= X_imax - X_i⁰ = X_i⁰- X_{imin .}

Интервалы варьирования равны, соответственно:

I₁= 35-30=5

I₂= 110-105=5

2.2.Перевод нижних и верхних значений уровней факторов в кодированный вид.

Перевод нижних и верхних значений уровней каждого из факторов в кодированный вид производится по формуле:

х_i= (X_i - X_i⁰ )/ I_i ,

где х_i –значение i-ого фактора на нижнем, верхнем или любом другом уровне в кодированном виде,

X_i – значение i-ого фактора на нижнем, верхнем или любом другом уровне в натуральном виде.

х_1min= (25-30)/5= -1,

х_1max= (35-30)/5=+1,

х_2min =(100-105)/5= -1,

х_2max=(110-105)/5=+1.

2.3. План ПФЭ для двух факторов.

План ПФЭ приведен в [табл.2.1].

Таблица 2.1.

План ПФЭ с результатом статистической обработки наблюдений.

Номер опыта	х1	х2	X1	X2											Sj2
1	2	3	4	5	6									7	8
1	+1	+1	35	110	10,72	11,86	10,94	12,08	10,03	12,77	10,72	13,22	10,03	11,37	1,3435
2	-1	+1	25	110	14,19	18,48	13,86	18,81	15,84	18,48	16,17	17,49	16,5	16,65	3,3517
3	+1	-1	35	100	8,32	11,48	8,91	10,89	8,71	10,3	9,5	11,29	8,32	9,75	1,6133
4	-1	-1	25	100	13,05	15,08	12,18	15,66	13,34	15,37	12,18	15,66	12,76	13,92	2,2497

2.4. Имитационный эксперимент.

Проведем имитационный эксперимент в соответствии с планом, делая по n=9 наблюдений в каждом опыте (точке плана).

Значение выходного параметра в j-ом опыте при k-м наблюдении определяется по формуле:

,

где α – коэффициент, определяющий относительную погрешность наблюдений, для процессов деревообработки α = 0,02;

У_j^*- значение выходного параметра j-м опыте;

R_jk - число в таблице случайных чисел, находящееся на j-й строке в k-м столбце (берём 21-ый и 22-ой столбцы).

Первому наблюдению соответствует значение выходного параметра:

У₁₁=11,4•[1+(-1)¹•0,02•3]=10,72

У₂₁=16,5•[1+(-1)¹•0,02•7]= 14,19

У₃₁=9,9•[1+(-1)¹•0,02•8]=8,32

У₄₁=14,5•[1+(-1)¹•0,02•5]=13,05

и так далее.

Результаты эксперимента запишем в виде табл. 2.1

2.5. Обработка результатов наблюдений для каждого опыта.

Среднее значение выходного параметра в каждом опыте определяется по формуле:

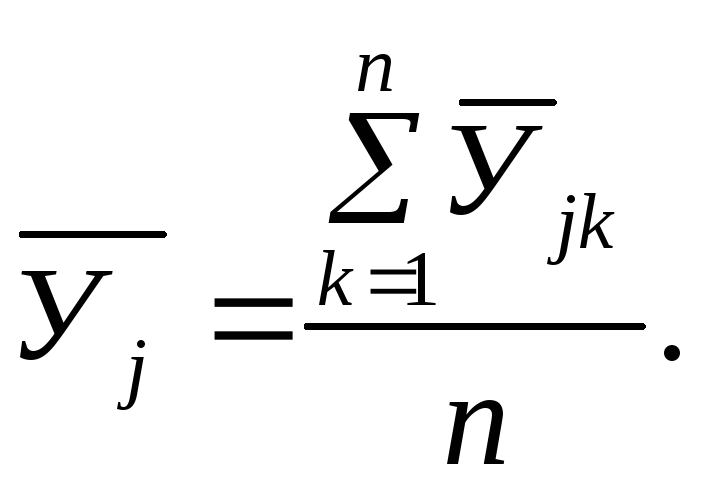
Аналогично для остальных опытов.

Дисперсии вычисляются по формуле:

Так, для первого опыта:

= [(10,72-11,37)²+ (11,86-11,37)²+ (10,94-11,37)²+ (12,08-11,37)²+ (10,03-11,37)²+(12,77-11,37)²+ (10,72-11,37)²+ (13,22-11,37)²+ (10,33-11,37)²]=1,3435

Аналогично для остальных опытов. Результаты заносим в таблицу 2.1.

2.6.Определение необходимого количества наблюдений для достижения требуемой точности с 95% уровнем достоверности.

Необходимое количество наблюдений n^* для достижения требуемой точности при доверительной вероятности p=0,95 определим для опыта, в котором дисперсия S²_j* максимальна, то есть для второго опыта.

Пусть максимальная относительная погрешность определителя выходного параметра равна ε =10%. Тогда по формуле:

,

где - среднее значение выходного параметра в j^*-м опыте.

Максимальная абсолютная погрешность

∆=10•16,65/100=1,665

Далее проверяем выполнение условия:

,

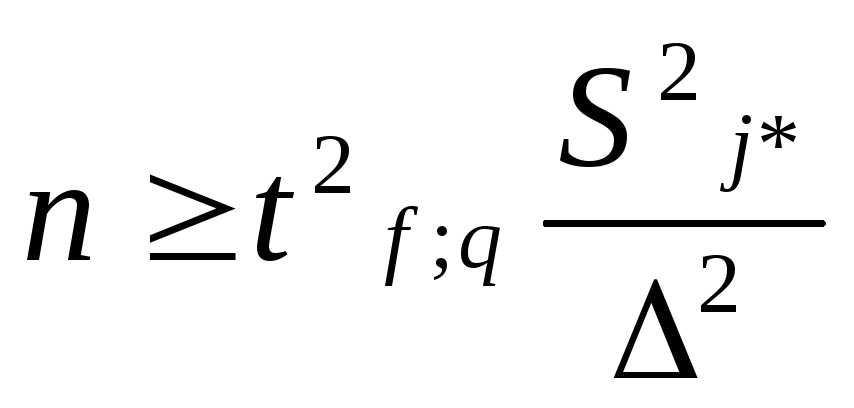где t_t;q – критерий Стьюдента для уровня значимости q=1-0,95=0,05 и числа степеней свободы f=n-1=9-1=8;t _табл.=2,306

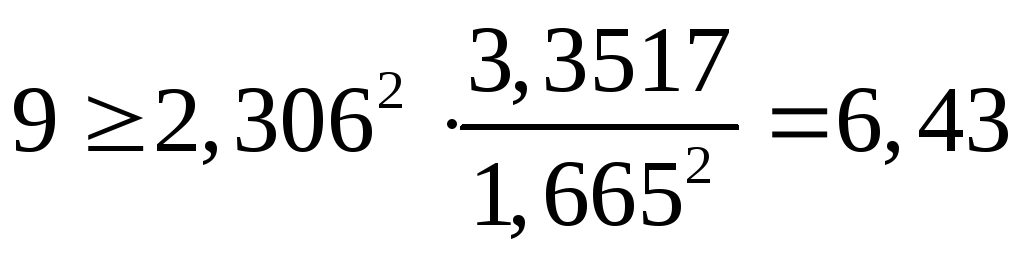
Поскольку условие выполняется, то выбранное первоначальное количество наблюдений n=9 является достаточным.

2.7.Оценка однородности дисперсии в различных опытах.

Оценим однородность дисперсии в различных опытах, для чего проверим выполнение условия:

,

где S²_j* - максимальная дисперсия;

G_f;N – критерий Кохрена для 95%-го уровня достоверности( уровень значимости 0,05), числа степеней свободы числителя f=(n-1) и знаменателя N;f=8,N=4

G_f;N ≥ 3,3517/(1,3435+3,3517+1,6133+2,2497) =0,39

G_{8; 4}=0,52>0,39

условие выполняется, дисперсии однородны.

2.8.Определение обобщенной дисперсии.

Обобщенная дисперсия (дисперсия воспроизводимости) находится по формуле:

S² = (1,3435+3,3517+1,6133+2,2497)/4=2,1396

2.9.Определение коэффициентов регрессионного уравнения.

Коэффициенты регрессионного уравнения определяются по формулам:

,

,

.

b₀= (11,37+16,65+9,75+13,92)/4=12,92;

b₁= (11,37-16,65+9,75-13,92)/4= -2,36;

b₂= (11,37+16,65-9,75-13,92)/4=1,09.

2.10.Оценка значимости членов регрессионного уравнения.

Оценим значимость членов регрессионного уравнения по условию :

,

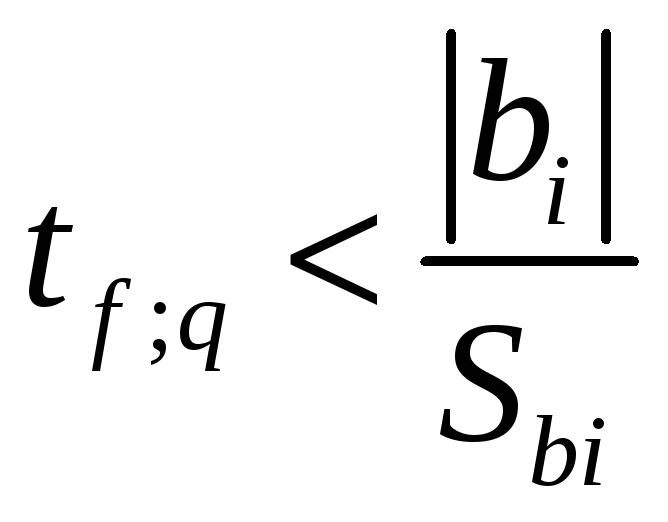где - дисперсия коэффициентов;

где , , = 2,036

То есть коэффициент значим, если он больше, чем 0,244•2,036=0,497.

12,92>0,497

|-2,36|>0,497

1,09>0,497

Все коэффициенты значимы.

2.11.Регрессинное уравнение.

Так как коэффициенты, определенные выше, больше чем 0,497, то регрессионное уравнение в кодированном виде будет содержать все члены выражения:

2.12.Проверка адекватности регрессионного уравнения.

Для проверки адекватности полученного регрессионного уравнения определим дисперсию адекватности:

,

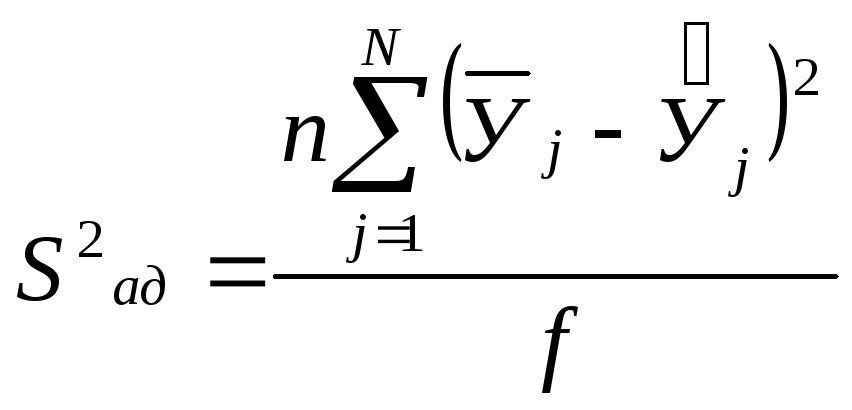где- значение выходного параметра в j-м опыте, рассчитанное по регрессионному уравнению;

f – число степеней свободы выборки.

Найдем предварительно значение для всех точек плана. Результаты представлены в табл. 2.2, где приведены также значения выходного параметра , полученные экспериментально для всех точек плана.

Таблица 2.2

Результаты расчета выходного параметра по регрессионному уравнению:

Номер опыта	x1	x2
1	2	3	4	5
1	+1	+1	11,37	11,65
2	-1	+1	16,65	16,37
3	+1	-1	9,75	9,47
4	-1	-1	13,92	14,19

Значения дисперсии адекватности для f=4-3=1 равно:

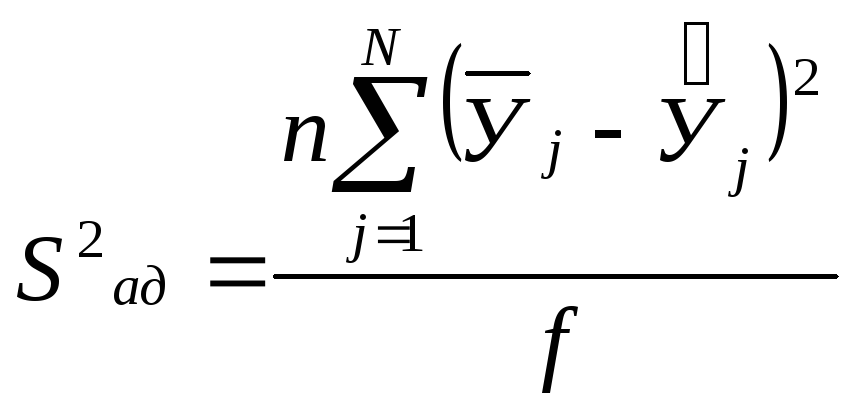
Правая часть выражения: равна 2,7729/2,1396=1,3, а левая представляет собой критерии Фишера F_{1; 32}=4,16.

Таким образом, условие 4,16>1,3 удовлетворяется, и полученное регрессионное уравнение адекватно.

2.13. Перевод регрессионного уравнения из кодированного вида в натуральный.

,

где x_i- значение i-го фактора на нижнем, верхнем или любом другом уровне в кодированном виде; X_i- значение i-го фактора на нижнем, верхнем и любом другом уровне в натуральном виде; X_iº- основной уровень i-го фактора; I_i- интервал варьирования i-го фактора.

То есть

X₁=5x₁+30 X₂=5x₂+105

x₁= x₂=

2.14. Вывод: Анализ полученного регрессионного уравнения показывает, что на изменение блеска покрытия большее влияние оказывает вязкость лака; причём, чем выше вязкость лака, тем меньше блеск покрытия. Чем больше расход лака, тем больше величина блеска, а поэтому меньше вязкость лака.

Список использованной литературы.

1. Чубов А.Б. Основы научных исследований. Методические указания по выполнению курсовой работы для студентов специальности 26.02. Санкт-Петербург: ЛТА, 1992.

2. Пижурин А. А., Розенблит М. С. Исследование процессов деревообработки. М.: Лесная промышленность, 1984.