Приклад виконання завдання з теми "Дослідження функцій однієї змінної"
За допомогою
функцій ППП Symbolic Math проведемо повне
дослідження функції однієї змінної(знайти
нулі функції, її асимптоти, точки
мінімуму та максимуму, точки перегину):
.
Визначити функцію та побудувати її графік.
>>syms x
>>y=(x^3+5)/(2*x^2+x-7)
y =
(x^3+5)/(2*x^2+x-7)
>>ezplot(y, [-10 10])
>>grid
Графік зображено на рис. 8.11.
Обчислити точки перетину з вісями координат:
>>y0=subs(y,’x’,0)% обчислюємо перетин з віссю Y
y0 =
0.7143
отже,
точка перетину з віссю
– це точка
Рис. 8.11. Графік функції x3/(2x2+x-7)
>>yzeros=solve(y)
% функція solve розв’язує
рівняння
,
% та знаходить як дійсні так і комплексні корені
yzeros =
5^(1/3)
1/2*5^(1/3)-1/2*i*3^(1/2)*5^(1/3)
1/2*5^(1/3)+1/2*i*3^(1/2)*5^(1/3)
Перетворимо символьні значення yzerosу числові:
>>yzeros=double(yzeros)
yzeros =
1.7100
0.8550 - 1.4809i
0.8550 + 1.4809i
Отже, наша функція
має лише один дійсний корінь, тому
перетином з віссю
є точка
.
За допомогою функціїplotнанесемо точки перетину на графік:
>>hold on
>>plot(0,y0,'ro',yzeros(1),0,'ro')
Результат виконаних команд міститься на рис. 8.12.
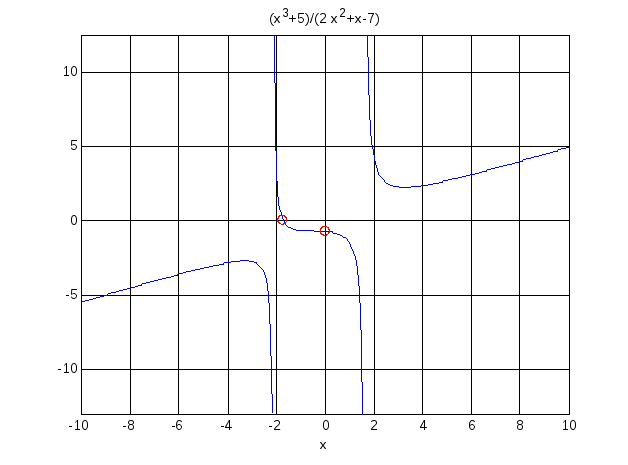
Рис. 8.12. Графік функції з нанесеними точками перетину з вісями
Дослідитиповедінку функції на нескінченності та з’ясувати питання про наявність асимптот.
>>limit(y, Inf)
ans =
Inf
>>limit(y, -Inf)
ans =
Inf
Отже, на нескінченності функція не обмежена, тому не має горизонтальних асимптот. Знайдемо вертикальні асимптоти, для чого потрібно обчислити нулі знаменника:
>>denom=(2*x^2+x-7)
denom =
2*x^2+x-7
>>denomzeros=double(solve(denom))
denomzeros =
1.6375
2.1375
Отже, функція має
дві вертикальні асимптоти:
та
.
Похилі асимптоти
шукаємо у вигляді
,
де
,
а
.
>>k1=limit(y/x,Inf), k2=limit(y/x,-Inf)
k1 =
1/2
k2 =
1/2
>>b1=limit((y-k1*x),Inf), b2=limit((y-k2*x),-Inf)
b1 =
1/4
b2 =
1/4
Отже, функція має
одну похилу асимптоту
.
Додамо знайдені асимптоти до графіка
(рис. 8.13):
>>plot(denomzeros(1)*[1 1], [-20 20],'r—','LineWidth',2)
>>plot(denomzeros(2)*[1 1], [-20 20],'r—','LineWidth',2)
>>Y=k1*x+b1 % похила асимптота
Y =
1/2*x-1/4
>>plot([-10 10],[subs(Y,'x',-10),subs(Y,'x',10)],'r',... 'LineWidth',2)
Рис. 8.13. Графік функції із асимптотами
Останні, три рази функція plot була викликана з ще двома аргументами. Пояснимо їх значення. Аргумент 'LineWidth' вказує на те, що буде змінена товщина лінії, а значення числового аргументу, що йде через кому після 'LineWidth', вказує товщину цієї лінії.
Обчислити екстремуми.
Обчислимо похідну від нашої функції:
>>dy=diff(y,'x')
dy =
3*x^2/(2*x^2+x-7)-(x^3+5)/(2*x^2+x-7)^2*(4*x+1)
спростимо цей вираз:
>>dy=simplify(dy)
dy =
(2*x^4+2*x^3-21*x^2-20*x-5)/(2*x^2+x-7)^2
>>pretty(dy)
4 3 2
2 x + 2 x - 21 x - 20 x – 5
------------------------------
2 2
(2 x + x - 7)
Обчислимо критичні
точки, розв’язавши рівняння
:
>>criticpts=double(solve(dy))
criticpts =
3.2501
3.3225
0.4638 + 0.1281i
0.4638 - 0.1281i
Нас інтересують
тільки дійсні значення змінної – це
і
.
З рис. 8.13. видно, що при
функція має локальний максимум, а при
- локальний мінімум. Нанесемо точки
мінімуму та максимуму на графік (рис.
8.14).
>>plot(criticpts(1),subs(y,'x',criticpts(1)),'ko',... criticpts(2),subs(y,'x',criticpts(2)),'ko')
Рис. 8.14. Графік функції з екстремумами
Обчислення точок перегину Обчислимо другу похідну від нашої функції:
>>d2y=diff(y,’x’,2)
d2y =
6*x/(2*x^2+x-7)-6*x^2/(2*x^2+x-7)^2*(4*x+1)+2*(x^3+5)/(2*x^2+x-7)^3*(4*x+1)^2-4*(x^3+5)/(2*x^2+x-7)^2
спростимо цей вираз:
>>d2y=simplify(d2y)
d2y =
6*(5*x^3+13*x^2+59*x+25)/(2*x^2+x-7)^3
>>pretty(d2y)
3 2
5 x + 13 x + 59 x + 25
6 ------------------------
2 3
(2 x + x - 7)
Розв’яжемо рівняння
:
>>inflectpts=double(solve(d2y))
inflectpts =
0.4625
1.0688 + 3.1095i
1.0688 - 3.1095i
Отже, функція має
єдину точку перегібу при
.
Нанесемо цю точку на графік функції:
>>plot(inflectpts(1),subs(y,’x’,inflectpts(1)),’ko’)
На рис 8.15 зображено остаточний вигляд графіка дослідженої нами функції. Назалишок розглянемо ще дві функції для роботи з графікою – це функція figure і функція subplot. Виклик першої приводить до створення порожнього графічного вікна, наприклад
>>figure
або
>>figure(n) % n – має числові значення з множини натуральних чисел
Рис. 8.15. Остаточний вигляд графіка функції
Корисно викликати цю функцію, коли є необхідність розмістити декілька графіків у різних вікнах. Якщо ж необхідно, щоб в одному графічному вікні було відображено декілька графіків, але на різних вісях, то саме для цього придатна функція subplot. Її викликають з трьома вхідними аргументами:
>> subplot(m,n,p), деm,n– кількість підграфіків по вертикалі і горизонталі, аp– номер графіка, який треба зробити текучим. Для демонстрації роботи функціїsubplotпобудуємо в одному вікні графік функції, яку ми дослідували, графіки її першої та другої похідних.
Виконаємо наступні команди:
>>subplot(2,2,1)
>>ezplot(y)
>> grid
На рис. 8.16 маємо графік функції, що досліджується.
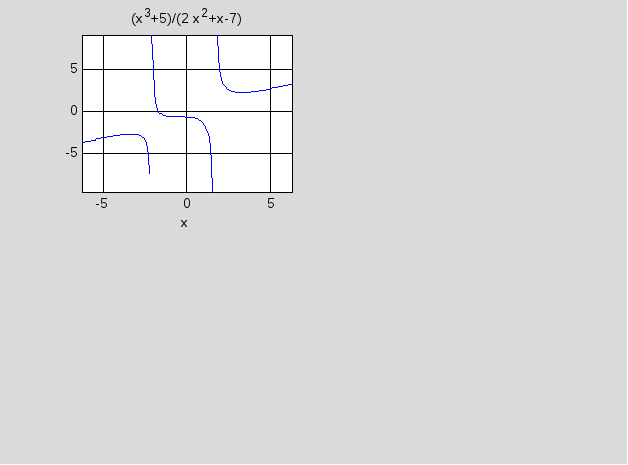
Рис. 8.16. Графік 1-ї функції, створений за допомогою команди subplot
Наступні команди приведуть до побудови графіка першої похідної (рис. 8.17)
>>subplot(2,2,2)
>>ezplot(dy)
>> grid
Рис. 8.17. Графіки двох функцій, створені за допомогою команди subplot
>>subplot(2,2,3)
>>ezplot(d2y)
>> grid
Остаточні графіки містяться на рис. 8.18.
Рис. 8.18. Графіки трьох функцій, створені за допомогою команди subplot