
- •Лекция 9. Обыкновенные дифференциальные уравнения первого порядка
- •2. Дифференциальные уравнения первого порядка
- •3. Уравнения с разделяющимися переменными Рассмотрим дифференциальное уравнение вида (4)
- •Общий интеграл его есть .
- •4. Однородные уравнения первого порядка
- •5. Линейные уравнения первого порядка.
- •6.Уравнения в полных дифференциалах
- •1. Линейные дифференциальные уравнения -го порядка
- •2. Линейный дифференциальный оператор и его свойства
- •3. Однородные линейные дифференциальные уравнения
- •4. Линейная независимость функций
- •5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •6. Метод Лагранжа (метод вариации произвольных постоянных)
- •7. Метод неопределенных коэффициентов
- •1. Числовые ряды. Сходимость и сумма рядов. Необходимый признак сходимости.
- •2. Достаточные признаки сходимости для рядов с положительными членами
- •3. Знакопеременные ряды. Признак сходимости Лейбница
- •Из (*) следует . (2)
- •Теорема умножения вероятностей:
- •Определение. Математическим ожиданием дсв х с законом распределения вероятностей
- •2.3 Планы практических занятий
Из (*) следует . (2)
Формула (2) называется формулой произведения вероятностей. В общем случае имеет место следующая теорема.
Теорема умножения вероятностей:
Пусть А1, А2,…An - некоторые события, тогда
![]() .
.
Определение. События![]() называются независимыми, если
вероятность появление любого из нихне
зависит от того произошли
или нет любые изостальных
событий. В
частности,если события
называются независимыми, если
вероятность появление любого из нихне
зависит от того произошли
или нет любые изостальных
событий. В
частности,если события
![]() и
и
![]() независимы, то
независимы, то
![]()
Теорема умножения вероятностей для независимых событий:
Пусть события
![]() независимы, тогда вероятность их
произведения равна произведению их
вероятностей, т.е.P(A1A2…An)=P(A1)P(A2)…P(An).
независимы, тогда вероятность их
произведения равна произведению их
вероятностей, т.е.P(A1A2…An)=P(A1)P(A2)…P(An).
Теорема. Пустьсобытия
А1,А2,…,Аn
попарно несовместны
и событие В может наступить
с одним из событий
![]() ,
,
![]() .
Тогда
.
Тогда
P(B)=P(A1)P(B/A1)+P(A2)P(B/A2)+…+P(An)P(B/An).
Эта формула называется формулой полной вероятности.
Теорема Байеса. Пустьсобытия
А1,А2,…,Аn
попарно несовместны
и событие В может наступить
с одним из событий
![]() ,
,
![]() .
Тогда
.
Тогда
![]() гдеР(В)находится по формуле полной
вероятности.
гдеР(В)находится по формуле полной
вероятности.
Повторение испытаний.
Пусть проводится
![]() независимых испытаний; причем, каждое
отдельное испытание имеет только два
исхода: рассматриваемое событие наступило
(удача) и рассматриваемое событие не
наступило (неудача), и в каждом отдельном
испытании вероятность наступления
рассматриваемого события (удачи)
постоянна и обозначается
независимых испытаний; причем, каждое
отдельное испытание имеет только два
исхода: рассматриваемое событие наступило
(удача) и рассматриваемое событие не
наступило (неудача), и в каждом отдельном
испытании вероятность наступления
рассматриваемого события (удачи)
постоянна и обозначается
![]() .Обозначим
.Обозначим
![]() - вероятность наступления рассматриваемого
события
- вероятность наступления рассматриваемого
события
![]() раз
в
раз
в
![]() независимых испытаниях. Справедлива
формула Бернулли:
независимых испытаниях. Справедлива
формула Бернулли:
![]() .
Здесь q есть вероятностьнаступления
неудачи в отдельном испытании и q
= 1 - p.
.
Здесь q есть вероятностьнаступления
неудачи в отдельном испытании и q
= 1 - p.
При достаточно больших значениях nискомую вероятность вычисляют приближенно
полокальной формуле Муавра – Лапласа:
![]() ,
где
,
где
![]() иq = 1 – p
иq = 1 – p
Функцией
![]() называется функция вида
называется функция вида
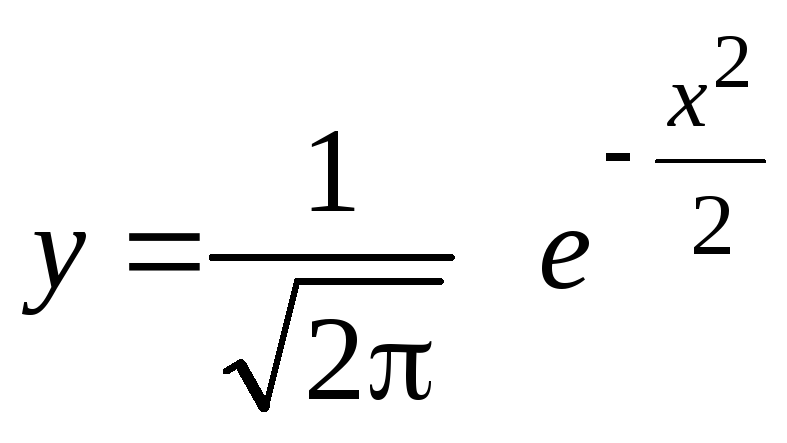 .Функция
.Функция
![]() табулируемая, т.е. есть таблица значений
этой функции.
табулируемая, т.е. есть таблица значений
этой функции.
Обозначим через Pn(k1,k2)вероятность того, что в схеме Бернулли
с параметрамиn, pчислоkнаступлений
событияАудовлетворяет
неравенству
![]() Назовем
функцией Лапласа функцию вида
Назовем
функцией Лапласа функцию вида
![]() .
Функция
.
Функция
![]() табулируема и в таблице даны значения
функции для
табулируема и в таблице даны значения
функции для
![]() ,
так как при
,
так как при
![]() выполняется условие
выполняется условие
![]() .Обозначим
.Обозначим
![]() .
Cправедлива приближеннаяинтегральная формула Муавра- Лапласа:
.
Cправедлива приближеннаяинтегральная формула Муавра- Лапласа:
![]() .
.
Пусть
![]() остается постоянным и
остается постоянным и
![]() .
Тогда для любого целого
.
Тогда для любого целого
![]() справедливаприближенная формула
Пуассона:
справедливаприближенная формула
Пуассона:![]()
Дискретные случайные величины (ДСВ). Закон распределения ДCВ
Определение. Случайнаявеличиной Хназывается величина, которая в результате испытания может принимать различие заранее неизвестные значения, причем только одно.
Определение. Случайнаявеличина Х называется дискретной (ДСВ), если она может принимать только конечное или счетное множество значений.
Пример: Число выигрышных билетов среди трех купленных билетов ; число бракованных изделий среди п изделий партии , количество ненастных дней в году и т.д.
Определение. Законом распределенияДСВ называется таблица,в одной строке которой стоят всевозможные значения этой величины, а в другой- вероятности их появления.
Обозначим:
![]() - значения ДСВ Х;
- значения ДСВ Х;
![]() ,
,
![]() .
.
Тогда закон распределения ДСВ имеет вид
|
|
|
|
… |
|
|
|
|
… |
Сумма всех вероятностей в законе
распределения ДСВ всегда равна единице:
![]() .
.
Пример. Пусть Х - число,выпавшее при бросании игральной кости, закон распределения Х имеет вид
-
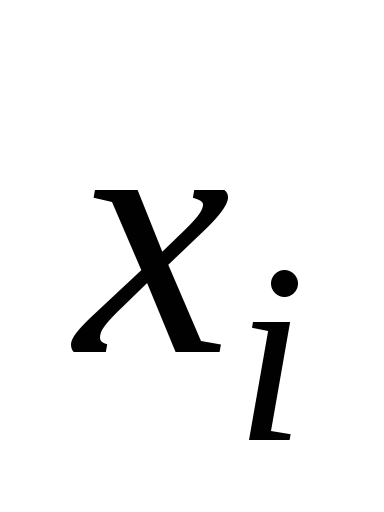
1
2
3
4
5
6
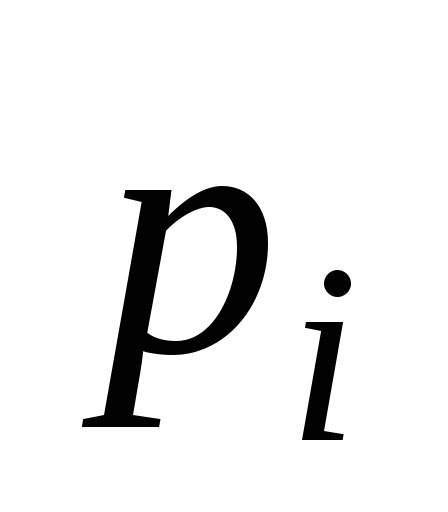
1/6
1/6
1/6
1/6
1/6
1/6
В данном примере
![]() .
.
Рассмотрим теперь некоторые стандартные
примеры ДСВ. Биномиальным
законом распределения
ДСВ Х
называется распределение
при котором
![]() определяются формулой Бернулли.
определяются формулой Бернулли.
|
|
0 |
1 |
… |
k |
… |
n-1 |
n |
|
|
|
npqn-1 |
… |
|
… |
npn-1 |
pn |
Закон распределения ДСВ
называется пуассоновским,
если вероятности
![]() определяются формулой
Пуассона.
определяются формулой
Пуассона.
Пусть Х- случайная величина, аx- любое действительное число.
Определение. Функцией распределения
вероятностиХназывается функция
действительного переменногох,равная вероятности того, что Х примет
значение меньшеx, т.е.
![]() Геометрически эта вероятность равна
вероятности попадания значенияхв промежуток
Геометрически эта вероятность равна
вероятности попадания значенияхв промежуток
![]()
Пример. Рассмотрим дискретную величинуХ со следующим законом распределения
-
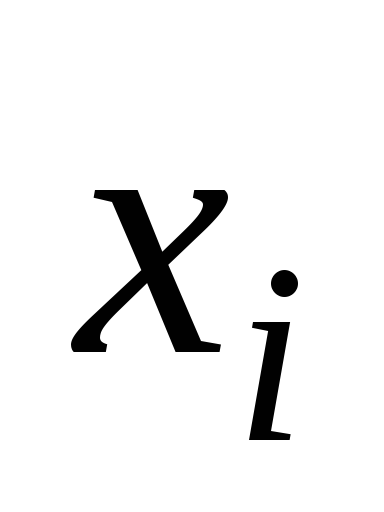
1
4
8
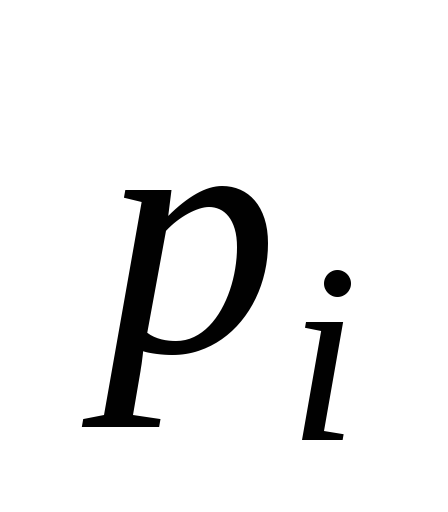
0,3
0,1
0,6
Найдем ее функцию распределения
вероятностей: а) если
![]() то
то
![]() (
(![]() )=0,
в)если
)=0,
в)если
![]() то
то
![]() (
(![]() )=
)=![]() (
(![]() =1)=0,3;
c)если
=1)=0,3;
c)если
![]() то
то
![]() (
(![]() )=
)=![]() ((
((![]() =1)+(
=1)+(![]() =4))=0,3
+0,1=0,4;
=4))=0,3
+0,1=0,4;
d) если
![]() >8,
то
>8,
то
![]() (
(![]() )=
)=![]() ((
((![]() =1)+(
=1)+(![]() =4)+(
=4)+(![]() =8))=0,3+0,1+0,6=1.
=8))=0,3+0,1+0,6=1.
Окончательно получим, что
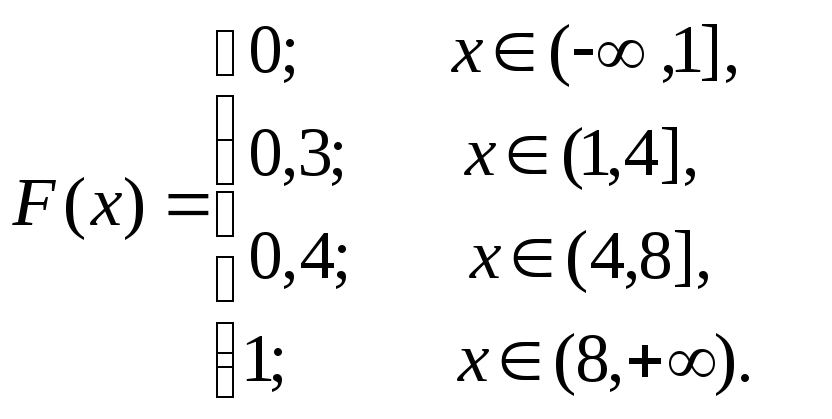
Рассмотрим свойства функции распределения вероятностей.
Свойство 1. Функция F(x) определена
на всей числовой оси и принимает свои
значение из промежутка [0,1]:
![]() 1.
Это свойство следует из определенияF(x) и свойств вероятности.
1.
Это свойство следует из определенияF(x) и свойств вероятности.
Свойство 2. Если
![]() любые числа, то вероятность того, что
значение Х попадет в промежуток
любые числа, то вероятность того, что
значение Х попадет в промежуток
![]() ,
равна
,
равна
![]()
Свойство 3.Функция
![]() не убывает для всех х.
не убывает для всех х.
Это свойство непосредственно следует
из предыдущего, поскольку при
![]() выполняется
выполняется
![]() .
.
Свойство 4. Для любой случайной величиныХ верно:
![]()
В частности, если всевозможные значения
Х принадлежит отрезку
![]() ,
то
,
то
![]() при
при
![]() >b
и
>b
и
![]() при
при
![]()
