Лабораторная работа 113 введение

Колебаниями называются процессы, в той или иной степени повторяющиеся во времени. При периодических колебаниях изменение наблюдаемой величины в точности повторяется через совершенно определенное время - период. Они описываются периодической функцией времени

(1)

где Т – период функции, n – произвольное целое число.

Колебание будет полным, если за кратчайшее время система полностью повторит свое движение. Время Т, в течение которого совершается одно полное колебание, является периодом колебания. Число полных колебаний в единицу времени называется частотой колебаний.

(Гц-герц) (2)

С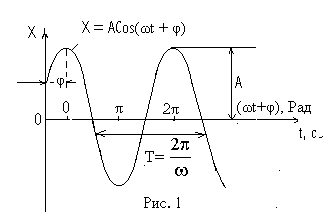истема, выведенная из положения равновесия и предоставленная самой себе, совершает свободные ( или собственные ) колебания. Если при этом энергия системы не изменяется, то ее колебания будут собственными незатухающими. Колебания с уменьшающейся энергией называются свободными затухающими. Колебания, совершаемые системой под воздействием внешней периодически изменяющейся силы, называются вынужденными.

Среди разнообразных колебаний, встречающихся в природе, основную и очень важную роль играют гармонические колебания (рис.1) представляют периодический процесс, в котором изменение наблюдаемой величины описывается функцией синуса ( или косинуса ):

или (3)

Здесь Х – отклонение ( смещение ) механической системы от положения равновесия. Наибольшее смещение А называется амплитудой колебаний. Аргумент синуса или косинуса (ωt + φ)определяет смещение в любой момент времени и называется фазой колебаний;φ– начальная фаза ( в моментt= 0). Величинаω, равная числу колебаний за 2πединиц времени, называется циклической ( или круговой) частотой. Она в 2π раз больше обычной частотыν:

илирадс^-1 (4)

Амплитуда А и начальная фаза φопределяются начальными условиями, т.е. смещением Х₀и скоростьюV₀в момент времениt= 0.

Система, совершающая гармонические колебания, называется гармоническим осциллятором. Для описания его колебаний составляют дифференциальное уравнение движения и, решая его, находят закон этих колебаний – зависимость смещения от времени.

Рассмотрим несколько простейших систем, совершающих гармонические колебания.

1. Пружинный маятник – тело массой m, способное совершать колебания под действием силы абсолютно упругой невесомой пружины (рис.2).

При смещении тела на расстояние Х от положения равновесия на него действует сила упругости пружины, направленная к положению равновесия:

F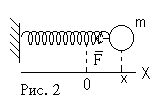= -kX(5)

где k– коэффициент упругости (жесткость) пружины. Уравнение второго закона Ньютона для тела имеет вид

mX= -kXили(6)

где – ускорение тела, равное второй производной смещения по времени).

Обозначив положительную величину k/mчерезω²₀, получим

(7)

Следовательно, движение тела под действием упругой силы описывается линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами без первой производной. Уравнение вида (7) называется уравнением гармонических колебаний. Общее решение уравнения (7)

X = A Cos(ω₀t + φ)(8)

является законом гармонического колебательного движения с собственной частотой

(9)

и периодом колебаний

. (10)

Таким образом, для того чтобы тело совершало гармонические колебания, действующая на него сила должна быть пропорциональна величине смещения тела и направлена в сторону, противоположную этому смещению. Если сила не является по своей природе упругой, но подчиняется закону (5), то ее называют “квазиупругой силой” (как бы упругой).

2. Физический маятник – это твердое тело, способное совершать колебания под действием своей силы тяжести вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр тяжести (масс) тела (рис.3).

При отклонении маятника от положения равновесия на угол φ возникает вращательный момент М, стремящийся вернуть его в положение равновесия:

М = - mga Sinφ,

где m– масса маятника,g– ускорение свободного падения,а– расстояние между точкой подвеса 0 и центром тяжести С.

Основной закон динамики вращательного движения в применении к физическому маятнику запишется в виде:

J = mga Sin φ, (11)

где J– момент инерции физического маятника относительно оси вращения 0,– угловое ускорение.

При малых угловых отклонениях Sin φ ≈ φ(в радианах) формула (11) переходит в уже известное нам уравнение гармонического колебания

. (12)

В данном случае круговая частота колебаний физического маятника выражается формулой

(13)

а период колебаний

(14)

3. Математический маятник – материальная точка, подвешенная на идеально гибкой, невесомой, нерастяжимой нити и способная совершать колебания в вертикальной плоскости под действием силы тяжести. Математический маятник представляет собой предельный случай физического маятника, вся масса которого сосредоточена в его центре масс, так что а = l– длина математического маятника, аJ=ml². Соответственно, круговая частота и период колебаний математического маятника равны

,(15)

Малые колебания рассмотренных маятников являются примерами изохронных колебаний, т.е. колебаний, частоты и периоды которых не зависят от амплитуды.

В общем случае период колебаний зависит от амплитуды, например, решив уравнение (2) для физического маятника, можно найти:

,(16)

где-наибольший угол отклонения от положения равновесия.

Из уравнений (14) и (15) следует, что математический маятник с длиной

L= (17)

будет иметь такой период колебаний, как и данный физический маятник. Величину (17) называют приведенной длиной физического маятника.

Точка на прямой (см. рис.3), соединяющий точку подвеса с центром масс, лежащая на расстоянииLот оси вращения 0, называется центром качания физического маятника.

По теореме Штейнера момент инерции маятника Jможет быть представлен в виде, (18)

где J₀– момент инерции относительно оси, параллельной оси вращения и проходящей через центр масс маятника. Подставив (18) в формулу (17), получим:

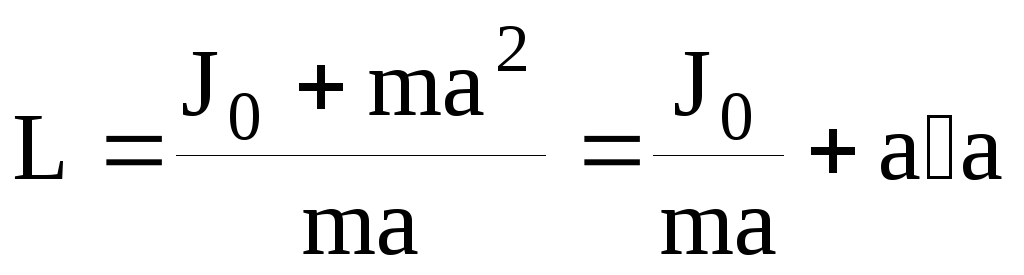, (19)

Следовательно, точка подвеса 0 и центр качания лежат по разные стороны от центра масс С. Точка подвеса и центр качания обладают свойством взаимности:при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания, т.е. приведенная длина и период колебаний маятника останутся прежними. Для доказательства этого утверждения достаточно, очевидно, показать равенство приведенных длинL= для двух положений маятника. Действительно, по формуле(19) имеем

и,

Из рис.3 следует:. Подставив это выражение в формулу для, найдем новую приведенную длину

и, следовательно, =Т.

На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника, в котором путем перераспределения масс можно добиться взаимности между двумя асимметричными точками подвеса относительно центра масс. Тогда при подвешивании за любую из этих двух точек подвеса период колебаний будет одинаков, а расстояние между точками будет равно LИзмерив период колебаний маятника и знаяL, можно по формуле

найти ускорение свободного падения g.