
книги / Экспериментальные методы в биомеханике
..pdf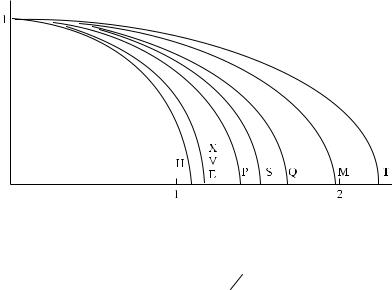
Рис. 7.13. Эллипсы структуры для различных образцов кости [70]
Величину R принято называть степенью анизотропии, она вычисляется как
α |
+ c |
12 |
|
||
R = |
|
|
|
. |
(7.14) |
α |
|
||||
|
− c |
|
|
||
Таким образом, отклонение от изотропии может быть описано при помощи некоторой единственной величины, например как отношение осей эллипса (см. формулу (7.14)) или как его эксцентриситет.
Итак, исходными измеряемыми величинами в работе [70] были относительная площадь кости AАb и длина проекции периметра границы на единицу площади поверхности образца JА(ω). Эти величины позволяли вычислить среднюю ширину трабекул W и среднее расстояние между порами Lb(ω). Мерой анизотропии образца служила величина R. Таким образом, существует несколько параметров, которые могут быть сравнимы с визуальным восприятием данного образца.
Повторяющиеся элементы вдоль какой-либо прямой линии в плоскости являются расстояниями между чередующимися элементами кость– пора (рис. 7.14). В сетке, состоящей из параллельных линий, или в прямоугольной сетке из точек каждое внутреннее пересечение дает одну оценку относительной длины траектории
261

|
в кости и в поре и, следователь- |
|||||
|
но, |
относительную |
площадь |
|||
|
кости AАb, а также одно наблю- |
|||||
|
дение |
проектируемой |
длины |
|||
|
границы. Даже в однородном |
|||||
|
образце эти |
расстояния |
вдоль |
|||
|
определенной |
линии |
способны |
|||
|
изменять свое среднее значение, |
|||||
|
и, так как образцы редко быва- |
|||||
|
ют изотропными, среднее зна- |
|||||
|
чение изменяется при измене- |
|||||
|
нии направления. В целом же |
|||||
Рис. 7.14. Иллюстрация повторения |
средняя повторяемость |
длины |
||||
для всех |
направлений |
на по- |
||||
длин в типичном образце кости [74] |
верхности образца определяется |
|||||
|
||||||
выражением L = π / BА. В |
среднем |
они |
составляют |
около |
||
1,25–1,5 мм, однако наименьшие могут быть менее 1 мм, а наибольшие – около 2 мм [74].
Сравнительно редко можно встретить площади исследуемых областей, превышающие 40 мм2, в пределах которой образец кости является однородным. Сторона таких областей была порядка 6–7 мм, что лишь в несколько раз больше L. В результате такая ситуация приводит к значительным колебаниям при измерениях. Более того, не существует строгого доказательства того, что бы позволило связать измерения на поверхности образца со свойствами трёхмерной структуры в случае, если данный образец не является однородным на некоторой допустимой глубине. Исходя из всего вышесказанного, можно сделать следующий вывод: для стереологических измерений образцы должны представлять собой кубик из однородной трабекулярной кости, чье ребро превышает L, как минимум, в несколько раз.
Подобные области легко можно найти в теле позвонка [69] и в концах большинства длинных трубчатых костей [72].Для подобных костей верна формула (7.1), то есть то, что относительный объем кости VVb численно равен ее относительной площади на поверхности шлифа AAb. Однако достаточно точное вычисление до-
262
полнительных параметров, таких как площадь поверхности пор в тестовом объеме SV, средняя ширина трабекул W и степени ориентации трабекулярной структуры, представляется невозможным из-за отсутствия соответствующей теории, за исключением некоторых простых случаев.
Стереологические формулировки, относящиеся к внутренним поверхностям, зачастую допускают изотропию внутренней структуры материала и, поскольку трабекулярная кость является почти всегда частично ориентированной, обычно подвержены влиянию ошибок, которые сложно оценить [74].
Наличие оси симметрии во внутренней структуре, если ее направление известно, существенно упрощает проблему. В структуре подобного типа поперечные сечения под правильными углами к данной оси проявляют изотропию; в частности, измерение среднего расстояния между порами будет одинаковым для всех направлений на поперечном сечении. Все сечения, перпендикулярные к первому, будут иметь одни и те же свойства; в частности, они будут иметь одни и те же графики средних расстояний между порами в кости в полярной системе координат как функции направления, и все они содержат в себе информацию, необходимую для определения полных свойств внутренней поверхности. В случае, если не возможно заранее определить осевую симметрию, тогда ситуация значительно усложняется.
Многие из вышеперечисленных трудностей в принципе предсказуемы. Огромное разнообразие структур в трабекулярных костях способствует уменьшению числа подходящих для обработки методами стереологии костных структур. Трабекулярная костная ткань может рассматриваться как статистически однородный композитный материал лишь для исключительно чётких картин, которые могут быть получены, например, с помощью растрового электронного микроскопа.
Однако же отсутствие метода для описания свойств анизотропных материалов, одновременно универсального и всегда эффективного, не является достаточно серьезной проблемой. Это объясняется тем, что общие свойства костной ткани намного больше значимы, чем ошибки, внесенные небрежностью измерений или только частичным допущением анизотропии [74].
263
7.3.О кривых и поверхностях второго порядка
Впредыдущем разделе данной главы упоминалось, что некоторые стереометрические зависимости могут быть описаны при помощи уравнения эллипса. В данном разделе мы напомним некоторые основные понятия из курса аналитической геометрии.
Общее уравнение второй степени относительно переменных x
иy может быть записано в следующем виде:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 . |
(7.15) |
Данное уравнение является общим уравнением линии второго порядка [9].
Уравнение эллипса является частным случаем уравнения (7.15), когда
A = |
1 |
, B = 0, C = |
1 |
, D = 0, E = 0, F = −1. |
|
a2 |
b2 |
||||
|
|
|
Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная [9].
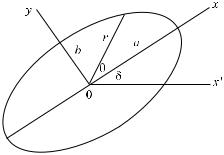
На рис. 7.15 показан эллипс, имеющий большую и малую полуоси a и b; большая полуось а расположена под углом δ к произвольно выбранному направлению 0x'. Предполагается, что ω = θ + δ, таким образом, радиус-вектор r расположен под углом ω
|
к произвольно |
выбранному |
|||||
|
направлению 0x', в котором |
||||||
|
будут производиться |
стерео- |
|||||
|
логические измерения, о чем |
||||||
|
будет сказано ниже. |
|
|||||
|
Каноническое |
уравнение |
|||||
|
эллипса в декартовой системе |
||||||
|
координат |
|
|
|
|
|
|
|
|
x2 |
+ |
y 2 |
|
= 1 |
(7.16) |
Рис. 7.15. Иллюстрация важнейших свойств |
|
a 2 |
b2 |
||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
эллипса [70]
264
может быть преобразовано для работы в полярной системе координат в уравнение вида
1 |
= |
cos 2 θ |
+ |
sin 2 θ |
(7.17) |
|
r 2 |
a 2 |
b 2 |
||||
|
|
|
или, после несложных тригонометрических преобразований, в следующем виде:
1 |
= |
a 2 |
+ b 2 |
− |
a 2 |
− b 2 |
cos 2θ . |
(7.18) |
|
r 2 |
2a 2 b 2 |
2a 2 b 2 |
|||||||
|
|
|
|
||||||
Очевидно, что величина, обратная квадрату радиуса-вектора эллипса, может быть представлена в виде косинусоиды в декартовой системе координат [9, 70].
Дальнейшее изложение будет касаться свойств поверхностей второго порядка. Принято устанавливать следующую классификацию поверхностей [9]:
1.Поверхность называется алгебраической, если в некоторой декартовой прямоугольной системе координат она определяется алгебраическим уравнением с тремя переменными.
2.Всякая не алгебраическая поверхность называется трансцендентной.
3.Алгебраическая поверхность называется поверхностью порядка n, если в некоторой декартовой прямоугольной системе коор-
динат она определяется алгебраическим уравнением степени n
стремя переменными.
Всилу данных определений поверхностью S второго порядка
называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a x2 |
+ a |
22 |
y 2 + a |
33 |
z 2 + 2a xy + 2a |
23 |
yz + 2a xz + |
(7.19) |
11 |
|
|
12 |
13 |
+2a14 x + 2a24 y + 2a34 z + a44 = 0,
вкотором, по крайней мере, один из коэффициентов a11 , a22 , a33 , a12 , a23 , a13 отличен от нуля.
265
Группа слагаемых |
a11x2 + a22 y2 + a33 z 2 + 2a12 xy + 2a23 yz + |
||
+ 2a13 xz называется |
группой старших членов |
этого уравнения, |
|
а группа слагаемых |
2a14 x + 2a24 y + 2a34 z + a44 – |
линейной частью. |
|
Данное определение аналогично определению гиперповерхности S второго порядка, которая определяется как геометрическое место точек x, удовлетворяющих уравнению вида
A(x, x) + 2B(x) + c = 0 |
(7.20) |
(см. [10]). Здесь под x подразумевается вектор n-мерного вещественного евклидова пространства; A(x, x) – не равная тождественно нулю квадратичная форма; B(x) – линейная форма; c – вещественное число.
Путем параллельных переносов можно упрощать группу линейных членов уравнения (7.19), не меняя при этом коэффициентов группы старших членов, а путем поворотов системы можно упрощать группу старших членов этого уравнения.
Величины
I |
1 |
= a + a |
22 |
+ a |
33 |
, I |
2 |
= |
a11 |
a12 |
+ |
a22 a23 |
+ |
a33 |
a13 |
, |
|||||||
|
11 |
|
|
|
|
|
a12 |
a22 |
|
a23 |
a33 |
|
a13 |
a33 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a11 |
a12 |
a13 |
|
|
|
|
a11 |
a12 |
a13 |
a14 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
I 3 = |
|
|
|
= |
a21 |
a22 |
a23 |
a 24 |
|
|
|
|
|
|
|||||||||
a21 a22 |
a23 |
, I 4 |
|
|
|
|
|
|
|||||||||||||||
a31 |
a32 |
a33 |
a34 |
|
|
|
|
|
|
||||||||||||||
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a41 |
a42 |
a43 |
a44 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(7.21)
являются инвариантами уравнения (7.19) поверхности второго порядка относительно преобразований декартовой системы координат. Аналогично инвариантами уравнения (7.20) гиперповерхности второго порядка являются коэффициенты характеристического
|
a11 |
… a1n |
многочлена матрицы A, где |
A = … |
… … , квадратичной формы |
|
|
|
|
an1 |
… ann |
266
A(x, x)
a
11
B = …an1
b1
и определитель расширенной матрицы B, где
… a1n b1
…… … (см. [10]).
…ann bn
…bn c
Поверхность второго порядка S будем называть центральной, если система линейных уравнений
a x |
0 |
+ a y |
0 |
+ a z |
0 |
+ a |
= 0 |
|
|
|
11 |
12 |
13 |
14 |
|
|
|||
a21 x0 |
+ a22 y0 |
+ a23 z0 + a24 = 0 |
(7.22) |
||||||
|
|
|
+ a32 y0 |
+ a33 z0 + a34 = 0 |
|
||||
a31 x0 |
|
||||||||
имеет единственное решение. Уравнения (7.22) называются уравнениями центра поверхности второго порядка, а точка (x0, y0, z0) называется центром этой поверхности [9].
Если начало координат перенести в центр поверхности, а затем перейти к новой системе координат путем параллельного переноса и поворота координатных осей, то уравнение поверхности (7.19) примет вид
a |
x2 + a |
22 |
y 2 + a |
33 |
z 2 + a = 0 . |
(7.23) |
11 |
|
|
14 |
|
Поскольку инвариант I3 для центральной поверхности отличен от нуля и его значение, вычисленное для уравнения (7.23), равно
а11a22a33 , то коэффициенты a11 ≠ 0 , a22 ≠ 0 , a33 ≠ 0 . Возможны следующие случаи:
1.Коэффициенты а11, а22, а33 одного знака, а коэффициент а44 отличен от нуля и противоположен знаку коэффициентов а11, а22, а33.
Вэтом случае поверхность является вещественным эллипсоидом.
2.Из четырех коэффициентов два одного знака, а два других – противоположного. Тогда поверхность будет однополостным гиперболоидом.
3.Знак одного из первых трех коэффициентов а11, а22, а33, а44 противоположен знаку остальных коэффициентов. Тогда поверхность называется двухполостным гиперболоидом.
4.Коэффициент а44 равен нулю. В этом случае поверхность является конусом второго порядка.
267
7.4.Некоторые необходимые сведения из тензорного исчисления
Вдальнейшем, при описании структуры костной ткани нам понадобится симметричный положительно определенный тензор второго ранга. Поэтому в данном разделе мы напомним некоторые основные понятия тензорного анализа.
Физические и геометрические величины, характеризующие состояние сплошной среды, не зависят от выбора системы координат, то есть являются инвариантными объектами. Однако эти величины удобно изучать в некоторой системе координат. При этом инвариантный объект определяется совокупностью величин, называемых его компонентами, которые зависят от системы координат. Такие многокомпонентные инвариантные объекты называют тензорами [7].
Инвариантный объект, который в системе декартовых осей
трехмерного пространства характеризуется девятью числами Tij, преобразующимися при повороте осей по закону
T ′ |
= α |
ki |
α |
T |
, |
(7.24) |
kl |
|
|
lj ij |
|
|
называется тензором второго ранга, а эти девять чисел с двумя в определенном порядке индексами называются его компонента-
ми [7].
Диада векторов (a b) – это простейший пример тензора второго ранга, образуемого по двум векторам a и b [4, 5]. Отметим, что для тензора второго ранга Т существует матричная форма представления, а именно:
T = |
t11 |
t12 |
t13 |
|
t12 |
t22 |
t23 |
. |
|
|
t13 |
t23 |
t33 |
|
Можно ввести понятие тензора второго ранга исходя из того, что тензорный характер какого-либо объекта можно распознать, подметив, что он определяется совокупностью чисел, которая образуется в результате операции над известными тензорами. Так, величина Tij, задающая преобразование вектора aj в вектор bi в форме произведения
268
bi = Tij a j |
(7.25) |
называется тензором второго ранга [7, 8].
Для доказательства этого утверждения рассмотрим теорему
об обратном тензорном признаке. Данная теорема гласит, что если в каждом ортонормированном базисе имеется совокупность 3p+q чи-
сел ci1…i p j1…jq такая, что в результате свертывания ее с произволь-
ным тензором ai1…i p ранга p получается тензор bj1…jq |
ранга q, то |
эта совокупность чисел образует тензор ранга p + q |
|
b j1…jq = ci1…ip j1…jq ai1…ip . |
(7.26) |
То есть если имеется равенство (7.25), в котором aj и bi – векторы, то совокупность девяти чисел Tij образует тензор второго ранга
[7].
Отметим также, что, в частности, если имеется равенство
b = cij aij = cij xi x j , |
(7.27) |
в котором aij = xi x j – диада, а b – скаляр, то совокупность девяти чисел Tij образует тензор второго ранга [7].
На основании соотношения (7.25) тензор второго ранга Tij можно определить как линейный оператор Т, посредством которого произвольному вектору a ставится в соответствие некоторый вектор b. Особую роль играет частный случай линейного оператора, когда
b = Ta = λ a , |
(7.28) |
где λ – скаляр, то есть когда направления векторов a и b совпадают, а модуль вектора b в λ раз отличается от модуля вектора a. В координатной форме равенство (7.28) запишется как
bi = λ ai . |
(7.29) |
Из сопоставления равенств (7.25) и (7.29) имеем |
|
Tij a j = λ ai . |
(7.30) |
269
Если вектор a при преобразовании посредством тензора Tij как линейного оператора изменяет только свою величину в λ раз, а направление его не меняется, то это направление называется главным направлением тензора Tij, а величина λ называется главным (собственным) значением тензора [7].
Симметричным называется такой тензор, транспонированный к которому совпадает с исходным [8], то есть
T′ ≡ TT = T . |
(7.31) |
Для симметричного тензора матрица его компонент в любом диадном базисе является симметричной, то есть T ij = T ji , Tij = Tji [8].
Для симметричного тензора результат скалярного умножения
на вектор а слева и справа одинаков: T a = a TT = a T . Собственные значения λα тензора Т всегда вещественны [7, 8].
Отметим также, что под положительной определённостью тензора понимается следующее. Положительно определенным называется симметричный тензор Т, если для всех ненулевых аргументов значение построенной на этом тензоре квадратичной формы положительно [8, 26], то есть
x E , x ≠ 0 |
x T x = T ij x x |
j |
> 0 . |
(7.32) |
3 |
i |
|
|
Симметричный тензор Т положительно определён тогда и только тогда, когда его собственные значения положительны:
λ α > 0 . |
(7.33) |
На практике для определения положительной определенности симметричного тензора Т удобно применять критерий Сильвестра: симметричный тензор положительно определен тогда и только тогда, когда положительны все главные миноры тензора [26].
Скалярное произведение тензоров A и B будет называться коммутативным, если выполняется следующее равенство:
A B = B A . |
(7.34) |
В противном случае скалярное произведение тензоров A и B
некоммутативно, то есть
270
