
книги / Труды IX Международной (XX Всероссийской) конференции по автоматизированному электроприводу АЭП-2016 , Пермь, 3-7 октября 2016 г
..pdf


ICPDS'2016 |
International Conference |
|
on Power Drives Systems (ICPDS’2016) |
|
___________________________________ |
|
IX Международная (XX Всероссийская) |
|
конференция по автоматизированному |
|
электроприводу АЭП-2016 |
Секция 4 ЭЛЕКТРИЧЕСКИЕ МАШИНЫ
____________________________________________________________________________________________________________________________
IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016
- 327 -
УДК 517.958; 536.2
Оптимальное проектирование броневых электромагнитов двухкоординатного электропривода
Ю.А. Бахвалов, В.В. Гречихин, О.А. Кравченко, А.Л. Юфанова
Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, Новочеркасск, Россия
Optimal design of shell-type electromagnets of xy-coordinate electric actuator
Y.A. Bakhvalov, V.V. Grechikhin, O.A. Kravchenko, A.L. Yufanova
The Platov South-Russia State Polytechnic University (NPI),
Novocherkassk, Russian Federation
Предложен метод оптимального проектирования бро- |
of optimal design of the shell-type electromagnet XY-coor- |
||
невых электромагнитов, основанный на решении методом |
dinate of electric actuator of magnetic levitation systems is |
||
конечных элементов обратных задач теории стационарного |
given. The method is highly efficient and can be used in design |
||
магнитного поля и на преобразовании ограничений на маг- |
of electromagnets that used not only in levitation systems, but |
||
нитную индукцию и подъемную силу в целевые функции. |
also for the design similar electrotechnical devices. Restriction |
||
Минимизация последних осуществляется численно мето- |
on the magnetic induction in the air gap can be omitted. |
||
дом градиентного спуска. |
Минимизация третьей целевой |
Ключевые слова: оптимальное проектирование, броневой |
|
функции (массы электромагнита) выполняется аналитиче- |
|||
электромагнит, электропривод, обратные задачи, магнитное |
|||
ски. Целевые функции ранжированы по важности. Метод |
|||
является модификацией метода решения многокритери- |
поле, методконечныхэлементов. |
||
альных задач – лексикографического метода упорядочения. |
Keywords: design optimization, electromagnets, actuators, |
||
Модификация учитывает |
особенности проектируемого |
inverse problems, magnetic fields, finite element analysis. |
|
объекта: каждая целевая функция зависит от ограниченно- |
|
||
го числа параметров объекта. Приведен пример оптималь- |
ВВЕДЕНИЕ |
||
ного проектирования броневого электромагнита систем |
|||
В различных областях техники в настоящее время |
|||
магнитной левитации двухкоординатного электропривода. |
|||
Предложенный метод отличается высокой эффективно- |
находят применение прецизионные двухкоординатные |
||
стью и может быть использован при проектировании элек- |
электроприводы (XY-приводы), позволяющие с высо- |
||
тромагнитов, применяемых не только в системах левита- |
кой точностью осуществлять перемещение тел в гори- |
||
ции, но и в других электротехнических устройствах. При |
зонтальной плоскости. Примером таких устройств |
||
этом ограничение на магнитную индукцию в воздушном |
являются несущие платформы для исследования об- |
||
зазоре может отсутствовать. |
разцов с помощью электронных микроскопов, изго- |
||
|
|
||
This article is devoted to the application of the method for |
товления интегральных микросхем и др. [1–5]. Для |
||
optimal design of the shell-type electromagnets based on the |
исключения механических контактов в таких устрой- |
||
solving inverse problems of stationary magnetic field theory |
ствах применяют магнитный подвес, который обеспе- |
||
by finite element method and on the transformation of con- |
чивает работу в различных средах и в вакууме, что |
||
straints on magnetic induction and a tractive force in the ob- |
невозможно с другими видами подвеса, включая воз- |
||
jective functions. Minimization of these objective functions is |
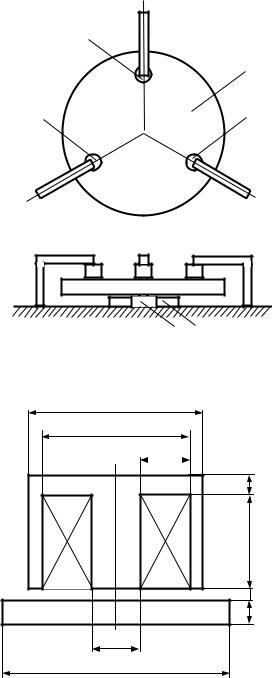
душные пленки (рис. 1) [6]. На рис. 1 обозначено: |
||
performed by gradient descent numerically. Minimizing third |
1 – электромагнит; 2 – платформа; 3 – линейный дви- |
||
objective function (mass of the electromagnet) is performed |
|||
гатель, осуществляющий перемещение по направле- |
|||
analytically. Objective functions are ranked by importance. |
|||
Method is a modification of the method for solving multicrite- |
нию 0y; 4 – линейный двигатель, осуществляющий |
||
ria problems and called the method of lexicographic ordering. |
перемещение по направлению 0x. |
||
The modification takes into account the features of the de- |
В системах магнитной левитации часто используют |
||
signed object; each objective function depends on a limited |
броневые электромагниты, обладающие минимальными |
||
number of parameters of the object. In addition, the example |
потоками рассеивания. |
||
____________________________________________________________________________________________________________________________
IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016
- 328 -
|
|
где B* |
– средняя магнитная индукция в воздушном зазо- |
||||||||||||
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ре δ, |
B* |
= 0,5 |
|
Тл; |
ε1 – |
допустимая относительная по- |
|||||||
1 |
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
грешность в определении магнитной индукции в зазоре; |
||||||||||||||
|
|
||||||||||||||
|
2 |
♦ подъемная сила F электромагнита должна быть не |
|||||||||||||
|
менее требуемой силы левитации F* |
|
|
|
|||||||||||
1 |
1 |
|
|
|
|
|
F* ≤ F ≤ (1+ ε2 (F* ))F* , |
|
(2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
где ε2 – допустимая относительная погрешность в опре- |
|||||||||||||
|
|
делении силы левитации. |
|
|
|
|
|
||||||||
|
|
В качестве целевой функции (критерия оптимально- |
|||||||||||||
|
|
сти) выберем массу электромагнита (без учета массы |
|||||||||||||
|
|
платформы). Для рассматриваемой конструкции (рис. 2) |
|||||||||||||
a) |
|
масса электромагнита определяется по формуле |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mem |
= (Sp |
+ Sp |
2 |
)h + πR32 h1 ρst + π(R22 − R12 )hρco , (3) |
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
где Sp1 |
и |
Sp2 |
– площади полюсов электромагнита; ρst, |
||||||||||
3 |
4 |
ρco – плотности ферромагнетика (стали) |
и меди соот- |
||||||||||||
ветственно. |
|
|
|
|
|
|
|
|
|
|
|||||
b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. Двухкоординатный электропривод с тремя системами |
|
I. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ |
|||||||||||||
магнитной левитации: а – вид сверху; б – вид сбоку |
Требуется определить магнитодвижущую силу ка- |
||||||||||||||
|
|
||||||||||||||
2R3 |
|
тушки (iw) и размеры электромагнита, при которых при |
|||||||||||||
|
заданном зазоре δ выполняются ограничения (1) и (2) |
||||||||||||||
|
|
||||||||||||||
2R2 |
|
и масса Mem (3) минимальна. |
|
|
|
|
|||||||||
l |
|
На основании ограничений введем дополнительно |
|||||||||||||
|
две целевых функции |
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
(n) |
− (1+ ε1 |
* |
* |
2 |
; |
|
|
h |
|
|
|
J1 (iw) = (Bδ |
|
(Bδ |
))Bδ ) |
|
||||||
|
|
|
|
|
J2 (Sp ) = (F(n) − (1+ ε2 (F* ))F* )2 , |
||||||||||
|
h |
где B(n) |
и F (n) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
– величины, найденные на n-м шаге ал- |
||||||||||||
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
горитма решения обратных задач теории стационарного |
|||||||||||||
|
δ |
магнитного поля [7]. Далее рассматриваются условно |
|||||||||||||
|
1 |
корректные обратные задачи (корректные по А.Н. Ти- |
|||||||||||||
|
h |
хонову) [8]. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2R1 |
|
Особенность конструкции устройства позволяет по- |
|||||||||||||
2R4 |
|
строить следующий итерационный алгоритм решения |
|||||||||||||
|
задачи. Для определения |
B(n) и |
F (n) |
будем решать по- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
Рис. 2. Центральное сечение броневого электромагнита |
следовательность прямых задач расчета стационарного |
||||||||||||||
|
|
плоскомеридианного магнитного поля. Минимизируя |
|||||||||||||
В данной работе предложен метод оптимального |
J1, определим МДС, Минимизируя J2, определим пло- |
||||||||||||||
проектирования броневых электромагнитов, который |
щадь сечения полюсов Sp1 и Sp2 |
. Минимизируя третью |
|||||||||||||
может быть использован при создании подобных элек- |
целевую |
функцию |
|
J3 |
= Mem , |
определим остальные |
|||||||||
тромагнитов различного применения (рис. 2). |
размеры электромагнита. |
|
|
|
|
|
|||||||||
Для того чтобы обеспечить работоспособность сис- |
|
|
|
|
|
||||||||||
темы магнитного подвеса, необходимо выбрать парамет- |
На основании рис. 2 получим следующие соотно- |
||||||||||||||
шения, связывающие параметры электромагнита: |
|||||||||||||||
ры электромагнита, при которых выполняются следую- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щие два условия: |
|
Sp = πR12 ; Sp |
|
= π(R32 − R22 ) ; h1 2πR1 |
= πR12 ; h1 = 0,5R1 ; |
||||||||||
♦ магнитная система ненасыщена, т.е. |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Bδ* ≤ B ≤ (1+ ε1 (Bδ* ))Bδ* , |
(1) |
R2 = R1 + l ; πR32 = Sp2 + πR22 ; π(R22 − R12 ) = π(2R1l + l2 ) . |
____________________________________________________________________________________________________________________________
IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016
- 329 -
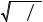

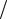
 h
h