Касательная плоскость и нормаль к поверхности

1°. Уравнения касательной плоскости и нормали для случая явного задания поверхности.

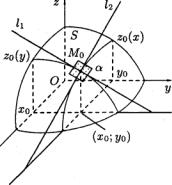
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция z = f(x;y) дифференцируема в точке (x0; у0) некоторой области D R2. Рассечем поверхность S, изображающую функцию z, плоскостями х = х0 и у = у0 (рис. 11).

Рис. 11

Плоскость х = x0 пересекает поверхность S по некоторой линии z0(y), уравнение которой получается подстановкой в выражение исходной функции z = =f(x;y) вместо х числа x0. Точка M0 (x0;y0,f(x0;y0)) принадлежит кривой z0(y). В силу дифференцируемой функции z в точке М0 функция z0(y) также является дифференцируемой в точке у =у0. Следовательно, в этой точке в плоскости х = х0 к кривой z0(y) может быть проведена касательная l1.

Проводя аналогичные рассуждения для сечения у = у0, построим касательную l2 к кривой z0(x) в точке х = x0- Прямые 11 и 12 определяют плоскость α , которая называется касательной плоскостью к поверхности S в точке М0.

Составим ее уравнение. Так как плоскость α проходит через точку Mo(x0; y0; z0), то ее уравнение может быть записано в виде

А(х - хо) + В(у - уо) + C(z - zo) = 0,

которое можно переписать так: z-z0 = A1(x – х0) + B1(y – у0) (1)

77

(разделив уравнение на -С и обозначив −AC = A1, −BC = B1 ).

Найдем A1 и B1.

Уравнения касательных 11 и 12 имеют вид

соответственно.

Касательная l1 лежит в плоскости α, следовательно, координаты всех точек l1 удовлетворяют уравнению (1). Этот факт можно записать в виде системы

Разрешая эту систему относительно B1, получим, что B1 = fy′(x0; y0 ) .Проводя аналогичные рассуждения для касательной l3, легко установить, что A1 = fx′(x0; y0 ) .

Подставив значения А1 и B1 в уравнение (1), получаем искомое уравнение касательной плоскости:

z − z0 = fx′(x0; y0 ) (x − x0 ) + fy′(x0; y0 ) (y − y0 )

Прямая, проходящая через точку М0 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.

Используя условие перпендикулярности прямой и плоскости, легко получить канонические уравнения нормали:

Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т. е. не особых, точек поверхности. Точка М0 поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.

Отсюда, применяя формулы (2) и (3), будем иметь: z-1=2(х-2)+2(у+1) или 2х+2у-z-1=0 —

2°. Уравнения касательной плоскости и нормали для случая неявного задания поверхности.

Если поверхность S задана уравнением F(x; у; z) = 0, то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:

— уравнение касательной плоскости и

78

— уравнения нормали.

Пример. Написать уравнения касательной плоскости и нормали к поверхности 3xyz − z2 = a2 в точке, для которой x=0, y=a.

Решение. Найдем аппликату точки касания, подставив x=0, у=а в уравнение поверхности: - z3 = а3, откуда z= -а. Таким образом, точка касания есть M(0; а; -а).

Обозначив через F(х, у, z) левую часть уравнения, найдем частные производные и их значения в точке М:

Fx '= 3yz,(Fx ')M = −3a2 , Fy '= 3xz,(Fy ')M = 0,

Fz '= 3xy − 3z2 ,(Fz ')M = −3a2.

Применяя формулы (4) и (5), получим: -3a²(x-0)+0(y-a)-3a²(z+a)=0 или х+z+а=0 —

уравнение касательной плоскости,

— уравнения нормали.

Формула Тейлора для функции нескольких переменных

Пусть функция f(х, у) имеет в окрестности точки (а; b) непрерывные частные производные всех порядков до (n+1)-го включительно. Тогда в рассматриваемой окрестности справедлива

формула Тейлора:

где

79

Частный случай формулы (1) при а=b=0 называется формулой Маклорена. Аналогичные формулы справедливы для функции трех и большего числа переменных.

Решение. Искомое приращение можно найти, применяя формулу (2). Вычислим предварительно последовательные частные производные и их значения в данной точке (1; 2):

Все дальнейшие производные тождественно равны нулю. Подставляя найденные результаты в формулу (2), получим:

Экстремум функции нескольких переменных

1°. Определение экстремума функции.

Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.

Пусть функция z = f(x; у) определена в некоторой области D, точка N(x0;y0) D.

Точка (x0;y0) называется точкой максимума функции z= f(x;y), если существует такая - окрестность точки (x0;y0), что для каждой точки (х;у), отличной от (x0;y0) из этой окрестности выполняется неравенство f(x;y) < f(x0;y0). На рисунке 12: N1 — точка максимума, a N2 — точка минимума функции z= f(x;y).

80

Приведенные условия эквивалентны следующим: пусть fx' (a,b) = f y' (a,b) = 0 и

A = fxx'' (a,b), B = fxy'' (a,b),C = f yy'' (a,b) . Составим дискриминант =AC — B².

Тогда:

1)если > 0, то функция имеет экстремум в точке Р (а; b) а именно максимум, если A<0 (или С<0), и минимум, если A>0 (или С>0);

2)если < 0, то экстремума в точке Р(а; b) нет;

3)если =0, то вопрос о наличии экстремума функции в точке Р(а; b) остается открытым (требуется дальнейшее исследование).

4°. Случай функции многих переменных. Для функции трех и большего числа переменных необходимые условия существования экстремума аналогичны условиям (1), а достаточные условия аналогичны условиям а), б), в) 3°.

Пример. Исследовать на экстремум функцию z=x³+3xy²-15x-12y. Решение. Найдем частные производные и составим систему уравнений (1):

или

x2 + y2 − 5 = 0,

xy − 2 = 0.

Решая систему, получим четыре стационарные точки:

P1( 1;2 ); P2( 2;1); P3( −1;−2 ); P4 ( −2;−1)

Найдем производные 2-го порядка

д2 z = 6 ,

дx2

д2 z = 6 y,

дxдy

д2 z = 6 x.

дy2

и составим дискриминант =AC — B² для каждой стационарной точки.

Значит в точке P1 экстремума нет.

2) Для точки P2: А=12, B=6, С=12; =144-36>0, A>0. В точке Р2 функция имеет минимум. Минимум этот равен значению функции при х=2, у=1: zmin=8+6-30-12=-28.

3) Для точки P3 : A= -6, B=-12, С= -6; = 36-144 <0. Экстремума нет.

4) Для точки Р4: A=-12, B=-6, С=-12; =144-36>0. B точке Р4 функция имеет максимум,

равный Zmах=-8-6+30+12=28.

5°. Условный экстремум. В простейшем случае условным экстремумом функции f(х,y) называется максимум или минимум этой функции, достигнутый при условии, что ее аргументы связаны уравнением φ(х,у)=0 (уравнение связи). Чтобы найти условный экстремум функции f(х, у) при наличии соотношения φ(х,у) = 0, составляют так называемую функцию Лагранжа

F(x,y)=f(x,y)+ λφ(x,y),

82

где λ — неопределенный постоянный множитель, и ищут обычный экстремум этой вспомогательной функции. Необходимые условия экстремума сводятся к системе трех уравнений

с тремя неизвестными х, у, λ, из которой можно, вообще говоря, определить эти неизвестные.

Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа

d 2F(x, y) = д2 F dx2 + 2 д2 F dxdy + д2F dy2

дx2 дxдy дy2

для испытуемой системы значений х, у, λ, полученной из (2) при условии, что dх и dу связаны уравнением

Именно, функция f(х,y) имеет условный максимум, если d²F< 0, и условный минимум, если d²F>0. В частности, если дискриминант для функции F(х,у} в стационарной точке положителен, то в этой точке имеется условный максимум функции f(х, у), если A< 0 (или С< 0), и условный минимум, если А > О (или С>0).

Аналогично находится условный экстремум функции трех или большего числа переменных при наличии одного или нескольких уравнений связи (число которых, однако, должно быть меньше числа переменных). Здесь приходится вводить в функцию Лагранжа столько неопределенных множителей, сколько имеется уравнений связи.

Пример. Найти экстремум функции z=6-4x-3y при условии, что переменные х и у удовлетворяют уравнению x²+y²=1.

Решение. Геометрически задача сводится к нахождению наибольшего и наименьшего значений аппликаты z плоскости z=6 - 4х - Зу для точек пересечения ее с цилиндром х2+у2=1.

Составляем функцию Лагранжа F(x,y)=6 -4x -3y+λ(x2+y2 -1).

Имеем ддFx = −4 + 2λx, ддFy = −3 + 2λy . Необходимые условия дают систему уравнений

− 4 + 2λx = 0,− 3 + 2λy = 0,

x2 + y2 = 1,

решая которую найдем:

то

83

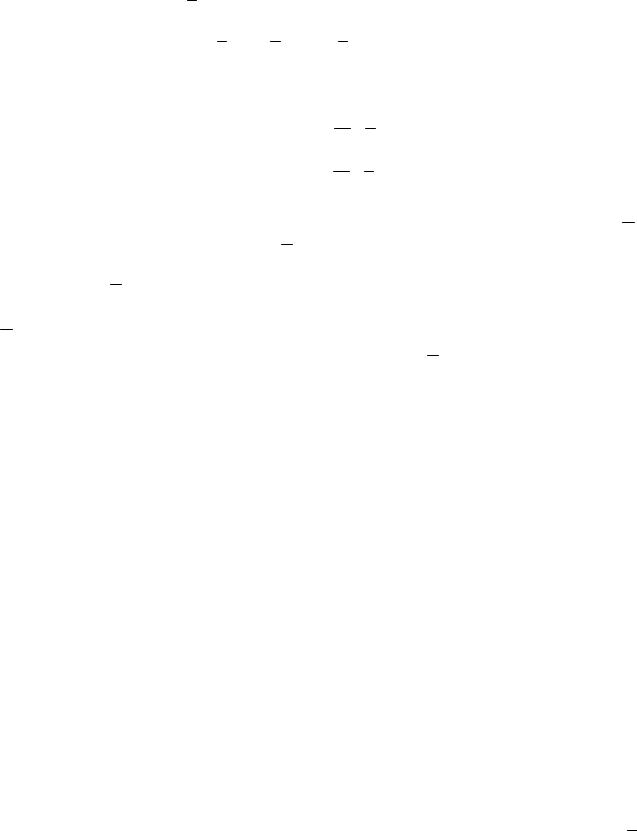
d²F=2λ(dx²+dy²).

Если λ = 52 , x = 54 и y = 53 , то d²F>0, и, следовательно, в этой точке функция имеет

условный минимум. Если λ = − 52 , x = − 54 и y = − 53 , то d²F<0, и, следовательно, в этой точке

функция имеет условный максимум. Таким образом,

zmax = 6 + 165 + 95 = 11, zmin = 6 − 165 − 95 = 1.

6°. Наибольшее и наименьшее значения функции.

Пусть функция z = f(x; у) определена и непрерывна в ограниченной замкнутой области D .

Тогда она достигает в некоторых точках D своего наибольшего М и наименьшего т значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных

внутри области D , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области

Dфункции z = f(x;y) состоит в следующем:

1.Найти все критические точки функции, принадлежащие D , и вычислить значения функции в них;

2.Найти наибольшее и наименьшее значения функции z = f(x; у) на границах области;

3.Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее

т.

Пример Определить наибольшее и наименьшее значения функции z=x²+y² -xy+x+y

в области

x ≤ 0, y ≤ 0, x + y ≥ −3 .

Решение. Указанная область есть треугольник (рис. 13). 1) Найдем стационарные точки:

z′x = 2x − y + 1 = 0,z′ = 2 y − x + 1 = 0,

y

отсюда x= -1, y= -1; получаем точку М(-1; -1).

В точке М значение функции zM = −1. Исследование на экстремум обязательно. 2) Исследуем функцию на границах области.

При х=0 имеем z=у²+у, и задача сводится к отысканию наибольшего и наименьшего значений этой функции одного аргумента на отрезке − 3 ≤ y ≥ 0 . Проведя исследование,

При у=0 имеем z=х²+х. Аналогично найдем, что (zнаиб )y=0 = 6 в точке (-3;0); (zнаим )y=0 = − 14 в

84