Второй метод представляет собой несколько видоизмененную схему первого метода и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:

на отрезке [а; b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; x].На этом отрезке величина А становится функцией х: А = A(x), т.е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х [а; b] – один из параметров величины А;

находим главную часть приращения A при изменении х на малую величину х = dx, т. е. находим дифференциал dA функции А = А(х): dA = f(x) dx, где f(x), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения);

считая, что dA ≈ A при x → 0, находим искомую величину путем интегрирования dA в пределах от а до b:

A(b) = A = ∫b f (x)dx.

a

Вычисление площадей плоских фигур

Прямоугольные координаты

Напомним, что, площадь криволинейной трапеции, расположенной «выше» оси абсцисс (f(x) ≥ 0), равна соответствующему определенному интегралу:

Отметим, что если криволинейная трапеция расположена «ниже» оси Ox (f (x) < 0), то ее площадь может быть найдена по формуле

Формулы (12) и (13) можно объединить в одну

S = ∫b y(x)dx

a

Площадь фигуры, ограниченной кривыми у = f1(x) и у = f2(x), прямыми х = а и х = b (при условии f2(x) ≥ f1(x)) (см. рис. 5), можно найти по формуле

S = ∫b f2 (x)dx − ∫b f1(x)dx = ∫b (f2 (x)− f1(x))dx .

Рис. 5.

Если плоская фигура имеет «сложную» форму (см. рис. 6), то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.

Если криволинейная трапеция ограничена прямыми у = с и у = d, осью Оу и непрерывной кривой х = ϕ (у) ≥ 0 (см. рис. 7), то ее площадь находится по формуле

49

S = ∫d x dy .

с

Пример. Найти площадь фигуры, ограниченной осью Ох и графиком функции у = х2 - 2х

при х [0; 3].

Решение:

Пример. Вычислить площадь фигуры, ограниченной эллипсом х = a cos t, у = b sin t.

Решение: Найдем сначала 1 площади S. Здесь х изменяется от 0 до a, следовательно, t

4

изменяется от π до 0 (см. рис. 9).

2

Рис. 9.

Находим:

50

Таким образом, 14 S = π 4ab . Значит, S = -π a b.•

Полярные координаты

Найдем площадь S криволинейного сектора, т.е. плоской фигуры, ограниченной непрерывной линией r = r(ϕ) и двумя лучами ϕ = α и ϕ = β (α < β), где r и ϕ – полярные координаты (см. рис. 10).

Рис. 10.

Дифференциал dS представляет собой главную часть приращения S при dϕ → 0 и равен площади кругового сектора ОАС (на рисунке 10 она заштрихована) радиуса r с центральным

углом dϕ. Поэтому dS = 12 r2 dϕ .

Интегрируя полученное равенство в пределах от ϕ = α до ϕ = β, получим искомую площадь

S= 1 ∫β r2 (ϕ )dϕ .

2 α

Пример. Найти площадь фигуры, ограниченной «трехлепестковой розой» Рис. 1 Решение:

Найдем сначала площадь половины одного лепестка «розы», т.е. 1 часть всей площади

6

фигуры:

Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, её следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 2, имеем:

51

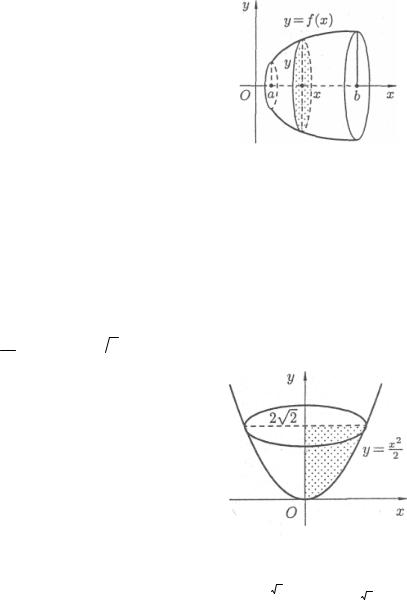
Объем тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = f(x) ≥ 0, отрезком а ≤ х ≤ b и прямыми х = а и х = b (см. рис.). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х [а, b]), есть круг с радиусом у = f(x). Следовательно, S(х) = π у2. Применяя формулу (16) объема тела по площади параллельных сечений, получаем

Vx = π ∫b y2dx

a

Если криволинейная трапеция ограничена графиком непрерывной функции х = ϕ(у) ≥ 0 и прямыми х = 0, у = с, у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой, равен

Vy = π ∫d x2dy .

c

Пример. Найти объем тела, образованного вращением фигуры, ограниченной линиями

y = x2 , х = 0, y = 2 2 вокруг оси Оу

2

Решение:

Вычисление объема тела по известным площадям параллельных сечений

Если известны площади S сечений какого-либо тела плоскостями, перпендикулярными некоторой оси, например оси Ox: S = S(x), а ≤ х ≤ b, то объем V этого тела можно найти по формуле

52