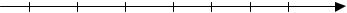
Модуль 7. Интегральное исчисление функций одной переменной.

Определенный интеграл

Понятие определенного интеграла и его свойства

Определенный интеграл как предел интегральной суммой

Пусть функция у = f(x) определена на отрезке [a; b], a < b. Выполним следующие действия.

С помощью точек x0 = a, x1, x2, …, xn = b (x0<x1< … <xn) разобьем отрезок [а, b] на п частичных отрезков [x0; x1], [x1; x2], …, [xn-1; xn] (рис. 1.).

c1 c2 ci cn x

О x0 = a, x1, xi-1 xi b = xn

Рис. 1.

Вкаждом частичном отрезке [xi-1; xi], i = 1, 2, …, n выберем произвольную точку ci [xi-1; xi],

ивычислим значение функции в ней, т.е. величину f(ci).

Умножим найденное значение функции f(ci) на длину xi = xi - xi-1 соответствующего частичного отрезка: f(ci) xi.

Составим сумму Sn всех таких произведений:

i =1

Сумма вида (1) называется интегральной суммой функции у = f(x) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max xi (i = 1, 2, …n).

5. Найдем предел интегральной суммы (1), когда n → ∞ так, что λ → 0.

Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется

определенным интегралом от функции у = f(x) на отрезке [а; b] и обозначается ∫b f (x)dx . Таким

a

образом,

Числа а и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, f(x) dx – подынтегральным выражением, х – переменной интегрирования, отрезок [а; b] – областью (отрезком) интегрирования.

Функция у = f(x), для которой на отрезке [а; b] существует определенный интеграл ∫b f (x)dx ,

a

называется интегрируемой на этом отрезке.

Если функция у= f(x) непрерывна на отрезке [а; b], то определенный интеграл ∫b f (x)dx

a

существует.

Непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

41

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (2).

1. Определенный интеграл не зависит от обозначения переменной интегрирования: ∫b f (x)dx = ∫b f (t)dt = ∫b f (z)dz

Это следует из того, что интегральная сумма (1), а, следовательно, и ее предел (2) не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: ∫a f (x)dx = 0

a

3. Для любого действительного числа с: ∫a c dx = c(b − a)

a

Геометрический смысл

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = f(x) ≥ 0. Фигура, ограниченная сверху графиком функции у = f(х), снизу – осью Ох, сбоку – прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [а; b] точками а = x0, x1, …, b = xn (x0 < x1 < … < xn) разобьем на n частичных отрезков [x0; x1], [x1;x2], …, [xn-1; xn] (рис. 2.). В каждом частичном отрезке [xi-1; xi], (i

= 1, 2, …, n) возьмем произвольную точку и вычислим значение функции в ней, т. е. f(ci).

Умножим значением функции f(ci) на длину xi = xi - xi-1 соответствующего частичного отрезка. Произведение f(ci) xi равно площади прямоугольника с основанием xi и высотой f(ci).

Сумма всех таких произведений

n

f(c1) x1 + f(c2) x2 + … + f(cn) xn = ∑ f (ci ) xi = Sn

i=1

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

n

S ≈ Sn = ∑ f (ci ) xi .

i=1

Суменьшением всех величин xi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится

площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max xi → 0:

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла. Формула Ньютона - Лейбница

Пусть функция у = f(x) интегрируема на отрезке [а; b].

Если функция у = f(x) непрерывна на отрезке [а; b] и F(x) – какая-либо её первообразная на [a; b] (F'(x) = f(x)), то имеет место формула

42

Равенство (4) называется формулой Ньютона - Лейбница.

Если ввести обозначение F(b) - F(a) = F(x) |ba , то формулу Ньютона-Лейбница (4) можно переписать так:

b

∫ f (x)dx = F(x)ba .

a

Формула Ньютона – Лейбница даёт удобный способ вычисления определённого интеграла. Чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке [а; b], надо найти её первообразную функцию F(x) и взять разность F(b) - F(a) значений этой первообразной на концах отрезка [а; b].

Основные свойства

1. Если с – постоянное число и функция f(x) интегрируема на [а; b], то

т.е. постоянный множитель с можно выносить за знак определенного интеграла.

2. Если функции f1(x) и f2(x) интегрируемы на [а; b], тогда интегрируема на [а; b] их сумма и

43

т. е. интеграл от суммы равен сумме интегралов. 3. ∫b f (x)dx = −∫a f (x)dx .

ab

4.Если функция f(x) интегрируема на [a; b] и а < с < b, то

∫b f (x)dx = ∫c f (x)dx + ∫b f (x)dx

т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).

«Теорема о среднем». Если функция f(x) непрерывна на отрезке [а; b], то существует точка с[а; b] такая, что

∫b f (x)dx = f (c) (b − a).

a

Свойство 5 («теорема о среднем»). При f(x) ≥ 0 имеет простой геометрический смысл: значение определённого интеграла равно, при некотором с (а; b), площади прямоугольника с

значением функции f(x) на отрезке [а; b].

1. Если функция f(x) сохраняет знак на отрезке [а; b], где, а < b, то интеграл ∫b f (x)dx имеет

a

тот же знак, что и функция. Так, если f(x) ≥ 0 на отрезке [а; b], то ∫b f (x)dx ≥ 0.

a

Неравенство между непрерывными функциями на отрезке [а; b], (а < b) можно интегрировать. Так, если f1(x) ≤ f2(x) при x [а; b], то

∫b f1(x)dx ≤ ∫b f2 (x)dx .

8. Если т и М – соответственно наименьшее и наибольшее значения функции у = f(x) на отрезке [а; b], (а < b), то

9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:

∫b f (x)dx ≤ ∫b f (x) dx ; a < b.

10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т.е.

Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

44