- •В.И. Гаркушенко теория автоматического управления
- •Введение
- •1. Задание на курсовую работу
- •1.1 Cиловые системы автоматического управления
- •1.1.1 Исходные данные
- •1.1.2 Техническое задание
- •1.2 Содержание пояснительной записки
- •2. Порядок выполнения работы
- •2.1 Расчет сау в линейном приближении
- •2.2 Расчет сау с учетом нелинейности
- •3. Практические рекомендации
- •3.1 Введение
- •3.2 Математическое описание функциональных элементов
- •3.2.1 Генератор постоянного тока
- •3.2.2 Тахогенератор
- •3.2.3 Электромашинный усилитель
- •3.2.4 Двигатель постоянного тока
- •3.3 Определение передаточных функций замкнутых систем
- •3.4 Определения коэффициента усиления электронного усилителя
- •3.5 Построение области устойчивости по коэффициенту усиления
- •3.5.1 Алгебраический метод построения области устойчивости
- •3.5.2 Частотный метод построения области устойчивости
- •3.6 Построение лах и лфх разомкнутой системы и определение запасов устойчивости замкнутой системы
- •3.7 Построение переходной характеристики замкнутой системы
- •3.8 Синтез последовательной коррекции с помощью лах и лфх
- •3.9 Электрическая схема корректирующего устройства
- •3.10 Синтез дискретного корректирующего устройства
- •3.10.1 Приближенный синтез дискретного корректирующего устройства
- •3.10.2 Синтез дискретного корректирующего устройства частотным методом
- •3.11 Определение параметров автоколебаний
- •3.12 Исследование системы на абсолютную устойчивость
- •Список литературы
- •Приложение а. Корректирующие цепи
- •Приложение б. Коэффициенты гармонической линеаризации нелинейных характеристик
- •Приложение в. Справочные данные
3.12 Исследование системы на абсолютную устойчивость
Если нелинейная
функция
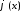 удовлетворяет секторному ограничению
удовлетворяет секторному ограничению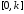 :
:
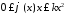 ,
,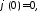
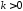 ,
,
например,
для нелинейностей типа № 1,2,3 (рис. 44), то
для проверки отсутствия автоколебаний
в замкнутой системе можно исследовать
систему на абсолютную устойчивость. 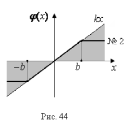
Состояние
равновесия замкнутой системы (рис. 39)
при
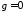 называется абсолютно устойчивым, если
оно асимптотически устойчиво в целом
при любой нелинейной функции
называется абсолютно устойчивым, если
оно асимптотически устойчиво в целом
при любой нелинейной функции ,
удовлетворяющей секторному ограничению
,
удовлетворяющей секторному ограничению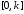 .
.
Для
определения абсолютной устойчивости
системы можно использовать частотный
критерий Попова. Практическая ценность
критерия Попова состоит в его простой
геометрической интерпретации. Для этого
введем преобразованную частотную
характеристику
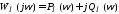 ,
у которой вещественная часть совпадает
с вещественной частью
,
у которой вещественная часть совпадает
с вещественной частью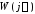 ,
а мнимая часть отличается на множитель
,
а мнимая часть отличается на множитель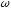 :
:
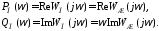
1. Рассмотрим основной случай, когда передаточная функция
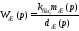
имеет
устойчивые полюса, т.е. корни уравнения
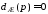 имеют отрицательные вещественные части.
Это соответствует вариантам схемА,
Б, В.
имеют отрицательные вещественные части.
Это соответствует вариантам схемА,
Б, В.
В этом случае критерий Попова формулируется следующим образом:
Состояние
равновесия замкнутой системы с одной
стационарной нелинейностью, удовлетворяющей
секторному ограничению
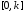 ,
при устойчивых корнях уравнения
,
при устойчивых корнях уравнения абсолютно устойчиво, если на комплексной
плоскости через точку
абсолютно устойчиво, если на комплексной
плоскости через точку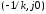 можно провести прямую так, чтобы
характеристика
можно провести прямую так, чтобы
характеристика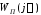 целиком лежала справа от этой прямой
(рис. 45).
целиком лежала справа от этой прямой
(рис. 45).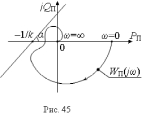
Построение
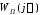 для рассмотренного выше примера можно
провести с помощью Script-файла:
для рассмотренного выше примера можно
провести с помощью Script-файла:
%Желаемая передаточная функция
Wgpas=75.5*tf([1/3.06 1],[1/0.7 1])*tf([1],[1/0.7 1])...
*tf([1],[1/45.31 1])*tf([1],[1/45.31 1]);
[Re,Im,w]=nyquist(Wgpas);
Wgpasn=squeeze(Re)+j*squeeze(w).*squeeze(Im);
figure(1);plot(Wgpasn);grid;%Преобразованная АФЧХ
Результат
построения приведен на рис. 46, из которого
следует, что для нелинейности № 1 со
значением
 можно провести прямую-1 через точку А
можно провести прямую-1 через точку А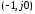 так, чтобы характеристика
так, чтобы характеристика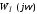 целиком лежала справа от этой прямой
и, следовательно, замкнутая система
абсолютно устойчива.
целиком лежала справа от этой прямой
и, следовательно, замкнутая система
абсолютно устойчива.
Это свойство
сохраняется для
 ,
где
,
где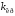 – критический коэффициент, соответствующий
точке В
– критический коэффициент, соответствующий
точке В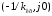 (прямая-2).
Здесь значение
(прямая-2).
Здесь значение
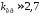 ,
что меньше ранее найденного коэффициента
,
что меньше ранее найденного коэффициента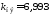 ,
соответствующего точке С
,
соответствующего точке С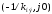 ,
поскольку
,
поскольку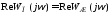 .
.
Таким образом,
согласно критерию Попова в замкнутой
системе отсутствуют автоколебания при
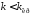 и она является абсолютно устойчивой. В
силу достаточности критерия Попова при
и она является абсолютно устойчивой. В
силу достаточности критерия Попова при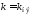 (точка С) абсолютная устойчивость не
гарантируется и согласно предыдущему,
возможно, что состояние равновесия
системы
устойчиво в большом и неустойчиво в
целом. Однако доказано [15], что в этом
случае автоколебания с частотой
(точка С) абсолютная устойчивость не
гарантируется и согласно предыдущему,
возможно, что состояние равновесия
системы
устойчиво в большом и неустойчиво в
целом. Однако доказано [15], что в этом
случае автоколебания с частотой
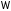 отсутствуют, если через точку С можно
провести прямую-3 слева от всех точек
на кривой
отсутствуют, если через точку С можно
провести прямую-3 слева от всех точек
на кривой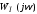 ,
которые соответствуют гармоникам
,
которые соответствуют гармоникам
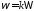 ,
,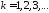
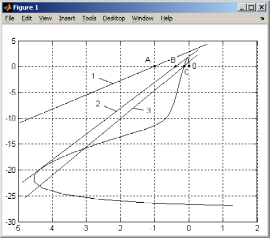
Рис. 46
2.
В случае, когда корни уравнения
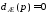 кроме устойчивых полюсов содержат
нулевые (схемыГ,
Д)
или неустойчивые полюса критерий Попова
формулируется следующим образом:
кроме устойчивых полюсов содержат
нулевые (схемыГ,
Д)
или неустойчивые полюса критерий Попова
формулируется следующим образом:
Состояние
равновесия замкнутой системы с одной
стационарной нелинейностью, удовлетворяющей
секторному ограничению
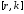 ,
при наличии нулевых и неустойчивых
корней уравнения
,
при наличии нулевых и неустойчивых
корней уравнения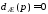 абсолютно устойчиво, если на комплексной
плоскости через точку
абсолютно устойчиво, если на комплексной
плоскости через точку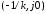 можно провести прямую так, чтобы
характеристика
можно провести прямую так, чтобы
характеристика ,
где
,
где
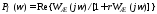 ,
,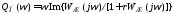 ,
целиком лежала справа от этой прямой.
,
целиком лежала справа от этой прямой.
Таким образом,
здесь необходимо, чтобы нелинейность
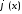 удовлетворяла секторному ограничению
удовлетворяла секторному ограничению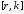 :
: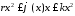 ,
,

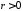 ,
,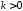 .
Этому условию не удовлетворяют
нелинейности № 1-3, поэтому применить
критерий Попова в этом случае не удается.
Однако для нелинейного элемента № 2
можно гарантировать отсутствие
автоколебаний
.
Этому условию не удовлетворяют
нелинейности № 1-3, поэтому применить
критерий Попова в этом случае не удается.
Однако для нелинейного элемента № 2
можно гарантировать отсутствие
автоколебаний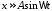 ,
если выполняется неравенство
,
если выполняется неравенство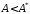 ,
где амплитуда
,
где амплитуда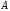 найдена методом гармонической
линеаризации, значение
найдена методом гармонической
линеаризации, значение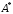 определяется из графика рис. 47.
определяется из графика рис. 47.