3.10.1 Приближенный синтез дискретного корректирующего устройства

Рассмотрим приближенный способ замены непрерывного регулятора с передаточной функцией

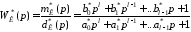
на дискретный регулятор с передаточной функцией

,

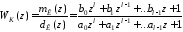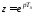где , где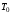– период дискретности.

Здесь период дискретности 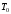рекомендуется выбирать из условия.

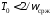Передаточная функция 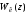находится в результате подстановки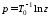в передаточную функцию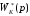. При малой величине периода дискретности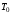функция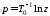допускает различные приближенные представления [9, с.73-78].

Рассмотрим распространенную на практике приближенную замену Тустена

.

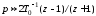Для рассмотренного ранее примера 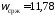рад/с, поэтому период дискретности должен удовлетворять условию 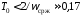с.

Определение 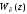и построение переходной характеристики замкнутой системы для различных значений периода дискретности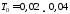с можно провести с помощьювспомогательной программы, составленной в Script-файле:

% Передаточная функция нескорректированной разомкнутой системы

Wpas=75.5*tf([0.4 1],[0.04 1])*tf([1],[0.2 1])*...

tf([1],[0.96 1])*tf([1],[0.38 1]);

% Непрерывное корректирующее устройство

Wk2=zpk([-25,-5,-3.06,-1.042],[-45.31,-45.31,-0.7,-0.7],2.3985*2.632/2.5);

% Модель непрерывного регулятора в пространстве состояний

sys=ss(Wk2);

% Дискретное корректирующее устройство при Т0=0,02;0,03;0.04с

for T0=0.02:0.01:0.04

Wkd=c2d(Wk2,T0,'tustin'); % построение дискретной модели

sim('DiskrKor'); % запуск на выполнение S-модели

figure(1);hold on; simplot(y)

figure(2);hold on; simplot(u)

end

Данная программа запускает на выполнение заранее составленную S-модель в системе SIMULINK, например, с именем DiskrKor, приведенную на рис. 30. Здесь на вход системы подается единичный скачок, для выходной координаты строится 5% трубка относительно установившегося значения .

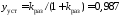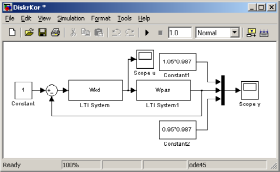
Рис. 30

Задание передаточных функций Wpas и Wkd в S-модели проводится с помощью блоков LTI System, выбор которых осуществляется с помощью окна Simulink Library Browser из раздела меню Control System Toolbox.

После раскрытия LTI блока указывается его имя Wpas , как показано на рис.31; аналогично задается блок Wkd.

Поскольку с помощью пиктограммы Print панели инструментов диалогового окна блока Scope не удается получить график желаемого вида, необходимо разместить массивы выходных данных в рабочей области системы MATLAB. Для этого необходимо у блока Scope на панели инструментов выбрать пиктограмму Parameters, выбрать вкладку Data history, установить флажок Save data to workspace и в текстовом поле Variable name задать имя переменной рабочей области системы MATLAB, которой присваиваются значения массива данных, как показано на рис.32 для блока Scope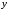 выходной переменной 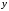. Аналогично в блокеScope устанавливается переменная .

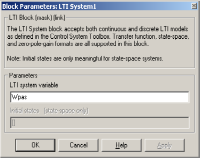
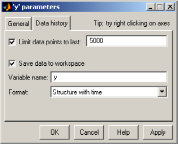
Рис. 31 Рис. 32

Для построения графиков в рабочей области системы MATLAB используется команда simplot.

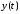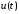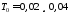В результате выполнения Script-файла строятся переходные процессы для выхода и кусочно-постоянного управленияприс, представленные на рис. 33 и рис.34 соответственно. Из переходных процессов рис. 33 следует, что в замкнутой системе сохраняются заданные показатели качества при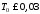с и нарушаются при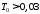с (значение).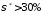

Если с помощью рассмотренного способа построения дискретной коррекции не удается обеспечить приемлемое значение 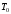, то можно доопределить выражение передаточной функции непрерывной коррекции с учетом влияния фиксатора нулевого порядка. Для этого необходимов качестве передаточной функции нескорректированной разомкнутой системы 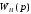принять

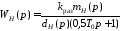
где апериодическое звено 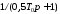имитирует фиксатор нулевого порядка, который вносит запаздывание в систему, и заново провести синтез непрерывной коррекции. Затем провести приближенный синтез дискретного корректирующего устройства.

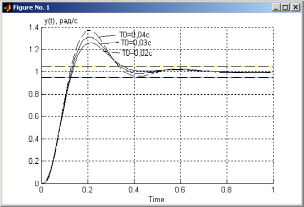
Рис. 33

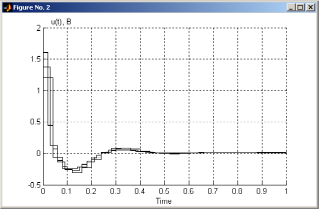
Рис. 34