2.8. Химические приложения определенного интеграла
Приведем в виде таблицы 11 химические приложения определенного интеграла.
Таблица 11.
|
Вычислить |
Формула |
|
Количество электричества, протекшее через электролизер за время Т |
|
|
Средняя и истинная теплоемкости |
|
|
Теплота испарения жидкости для температур, далеких от критической |
|
|
Теплота возгонки твердого тела |
|
|
Измерение энтропии при нагревании (охлаждении) от Т1 до Т2 при постоянном объеме или постоянном давлении |
|
,
,
Примеры:
При электролизе раствора CuSO4 силу тока в цепи, измеренную в амперах, изменяли по закону
,
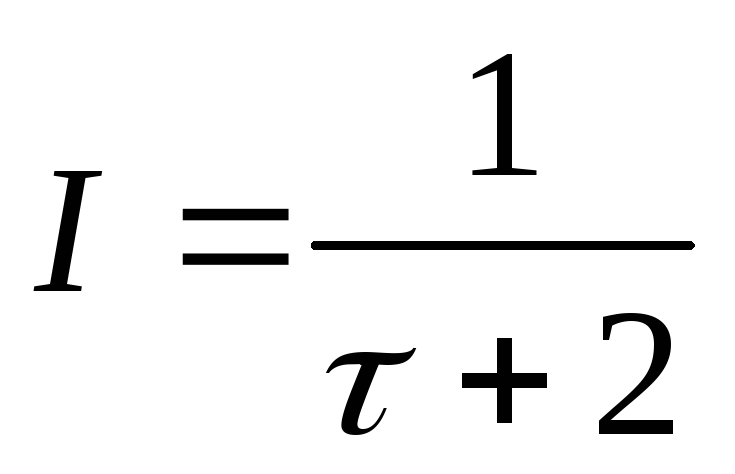где
- время электролиза, измеренное в часах.
Чему равна скорость осаждения меди в
начале и конце электролиза, если
электролиз длился 2 ч и выход по току
меди равен 100%? Определить количество
меди, образовавшееся за это время на
катоде.
Решение.
Скорость
электрохимической реакции определим,
согласно законам Фарадея, по формуле
.
Тогда по условию задачи для=0
и =2
ч получим
(мольс-1)
и
(мольс-1).
Соответственно количество меди, образовавшееся на катоде, найдем, предварительно определив количество электричества, протекшее через электролизер за это время:
(Кл).
(г).
Теплоты образования LiI при 298 К в газообразном и твердом состояниях составляют –67,0 и –271,3 кДж/моль соответственно. Зависимость теплоемкости твердого LiI от температуры выражается уравнением
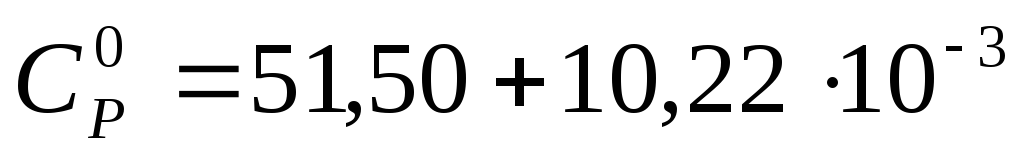Т.
Теплоемкость газообразногоLiI
Т. Определить теплоту возгонкиLiI
при 680 К.
Решение.
Теплоту
возгонки определяем по уравнению
.
Дж/моль.
Термический коэффициент объемного расширения ртути дается выражением:
,
гдеt
–
температура (0С)
и V0=V
при t=0.
Если показания идеального газового и
ртутного термометров совпадают при 0
и 1000
С, то какой кажущейся температуре по
ртутной шкале будет соответствовать
500
С по шкале идеального газового термометра?
Решение.
Вычисляется
с помощью формулы:
.
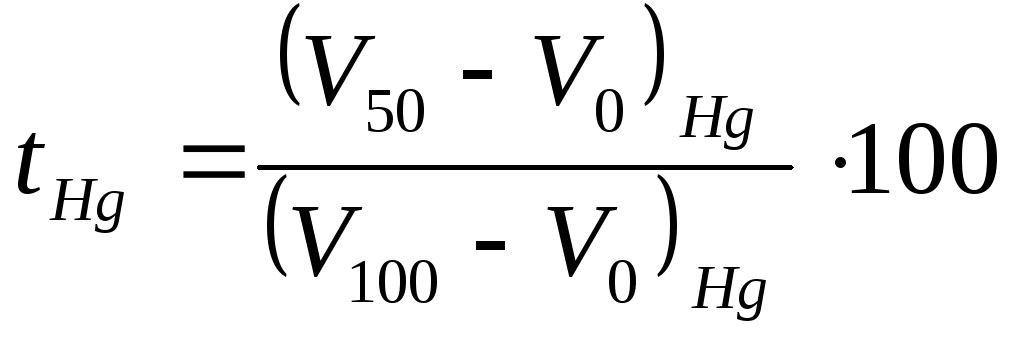Воспользуемся
формулой:
.
;
;
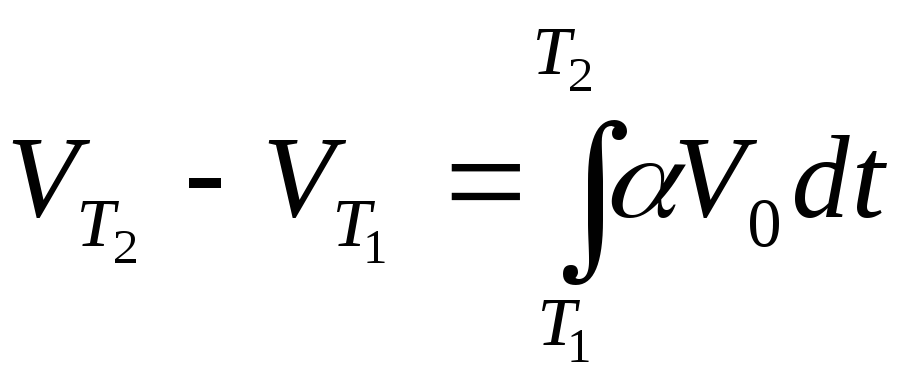Тогда
.
2.9. Задания для самопроверки №3
1. Постройте на бумаге в клетку систему координат, где единичный отрезок - 1см. Найдите приближенные значения следующих интервалов с помощью графиков подынтегральных функций:
|
a)
|
b) |
c) |
;
;
.
2. Пусть имеется
кардиоида
(рис.
см. приложение №1). Найти:
a)
площадь фигуры ограниченной кардиоидой
; Ответ:
.
b) длину дуги кардиоиды; Ответ: 8а.
3.
Пусть имеется
одна арка
циклоиды
,
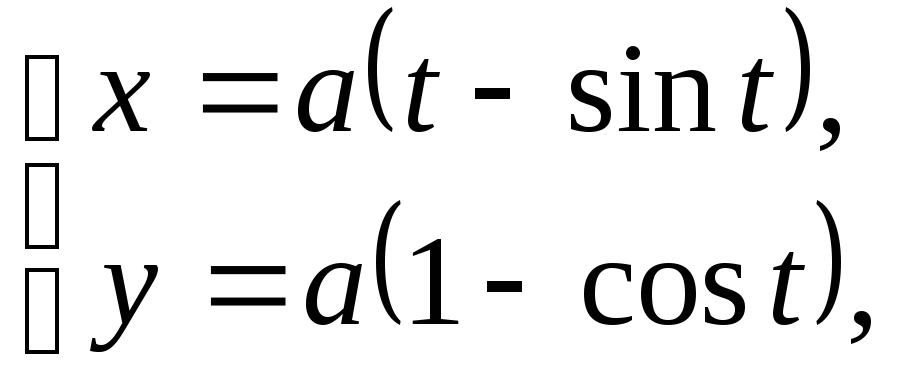
ограниченная осьюОх
(рис. см.
приложение №1). Найти:
a)
площадь циклоиды
Ответ:
.
b) длину дуги циклоиды; Ответ: 8а.
c) вычислить объём тела, образованного вращением вокруг оси Ох одной арки циклоиды. Ответ: 5π2а3.
4. Вычислить площадь
фигуры, ограниченной окружностями
и
.
Ответ:
.
5. Определить
площадь части круга
,
ограниченной кривыми
.
Ответ:
.
6.Найти силу давления
бензина, находящегося в цилиндрическом
баке высокой h
= 3,5 м и радиусом основания r
= 1,5 м, на его стенки, если
.
Ответ:
7.Найти работу, совершенную при выкачивании воды из емкости, имеющую форму полуцилиндра, длина которого a, радиус r.
Ответ:
8. Вычислить силу давления воды на пластину, имеющую форму параллелограмма с основанием а = 2 м и высота Н = 3 м, опущенную вертикально вниз на глубину 4 м, если основание параллельно поверхности воды. Плотность воды 1 т/м3.
Ответ: 156,8 кН.
9. Найти координаты центра масс однородной дуги окружности радиусом R с центром в начале координат, расположенной в первом квадранте.
Ответ:
(
;
).
10.
Найти координаты центра масс однородной
фигуры,
ограниченной линиями
.
Ответ:
(
;
).
11.
Вычислить работу, необходимую для того,
чтобы выкачать
воду из полусферического сосуда, диаметр
которого
20 м, если плотность воды
т/м3.
Ответ: 76969 кДж.
12.
Найти координаты центра масс однородной
плоской фигуры, ограниченной линиями
.
Ответ: (9;9).
13.
Производительность труда рабочего в
течение дня задается функцией
(ден.ед./ч.),
гдеt
–
время в часах от начала работы,
.
Найти функциюu=u(t),
выражающую объем продукции (в стоимостном
выражении) и его величину за рабочий
день.
Ответ: 4,53 ден. ед.
14.
Стоимость перевозки одной тонны груза
на один километр (тариф перевозки)
задается функцией
(ден.ед./км.).
Определите затраты на перевозку одной
тонны груза на расстояние 20 км.
Ответ: 23,98 ден. ед.
15.
Вычислить среднюю теплоемкость аммиака
в интервале температур от 298 до 1000 К.
Ответ: 45,79 Дж/(моль К).
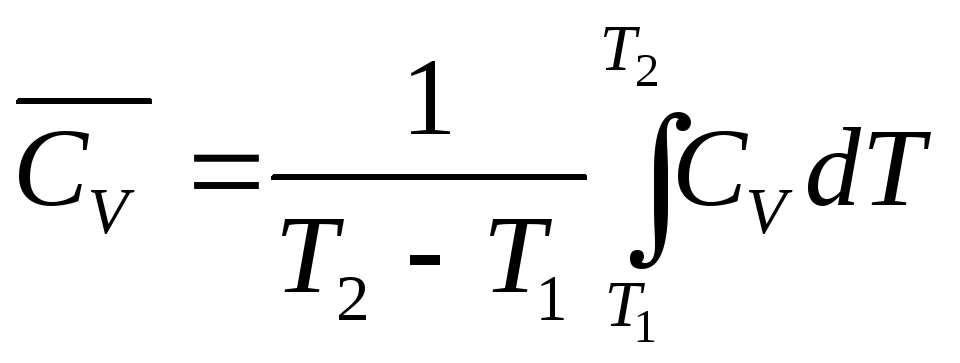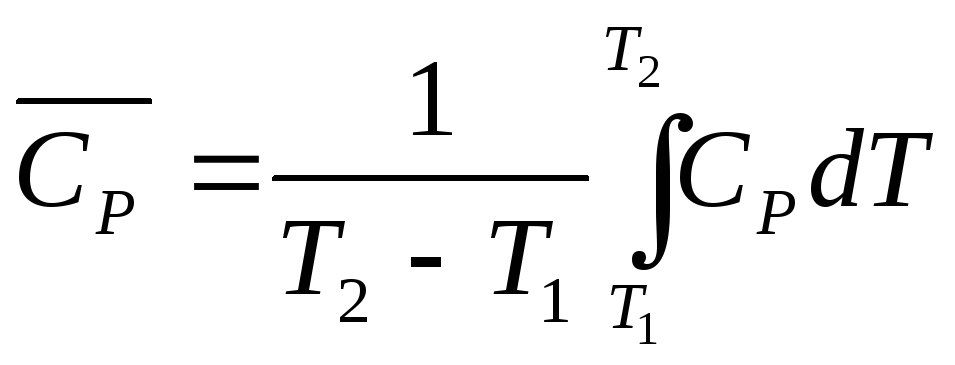
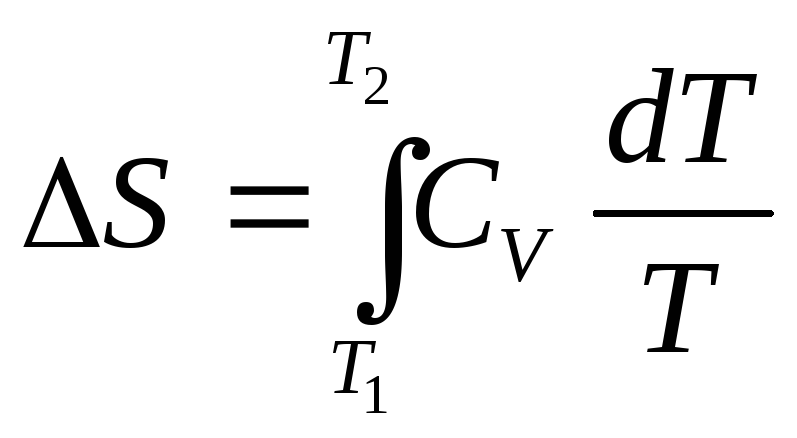