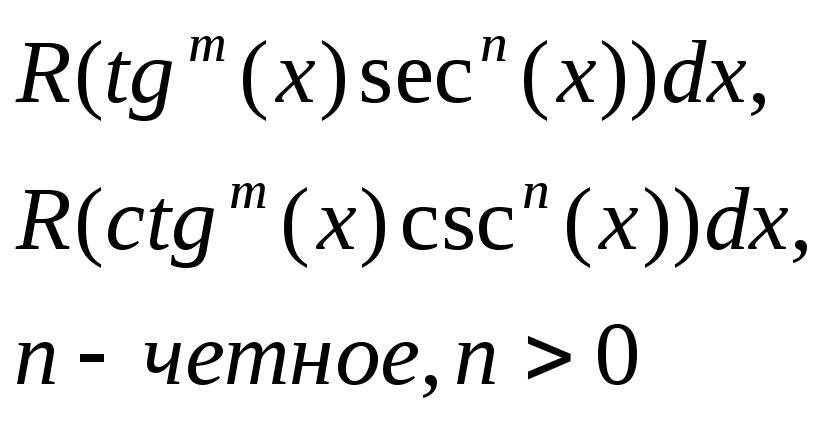1.4. Интегрирование тригонометрических функций

• Метод тождественных преобразований.

Примеры:

a)

b)

• Метод замены переменной.

Примеры:

c)

d)

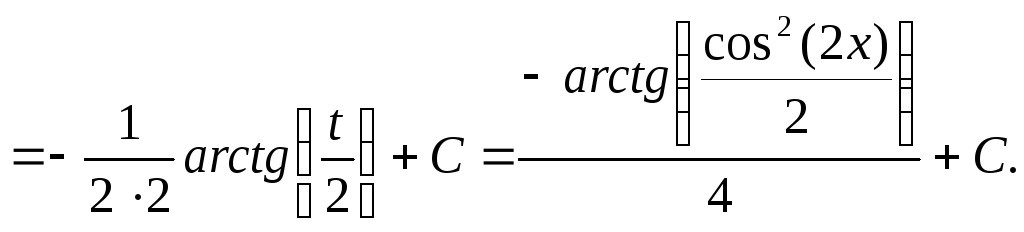
e)

• Метод универсальной тригонометрической подстановки (универсальной замены).

Примеры:

f)

g)

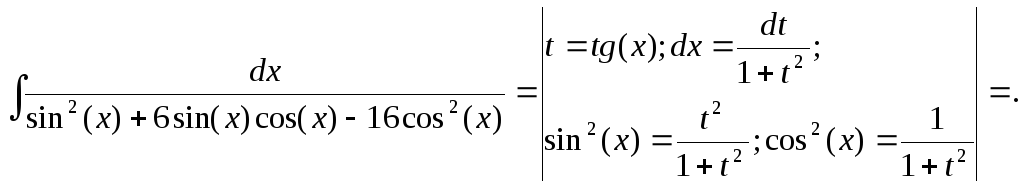
h)

Интеграл вычисляется методом неопределенных коэффициентов:

Получается:

.

Учитывая выше сказанное, представим основные типы тригонометрических функций в виде таблицы 4.

Таблица 4.

№	подынтегральное выражение	замена
1.		универсальная замена
2.
3.
4.
5.
6.		, ,
7.		Понижается степень по формуле
8.
9.		Применяются рекуррентные формулы

Здесь R – обозначение некоторой рациональной функции от переменных sin(x) и cos(x) . Функции sec(x)=1/cos(x) и csc(x)=cosec(x)=1/sin(x).

1.5. Интегрирование иррациональных функций

Выделяют четыре основных типа интегралов, содержащих иррациональные функции:

• Первый тип включает в себя интегралы, которые вычисляются методом замены переменной.

Примеры:

a)

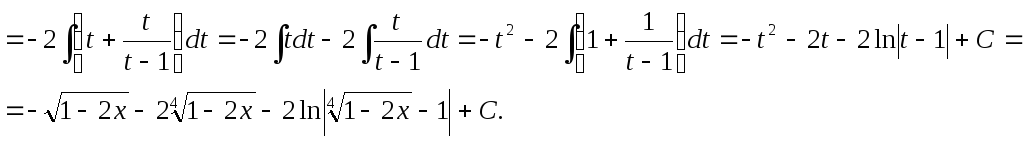
b)

с)

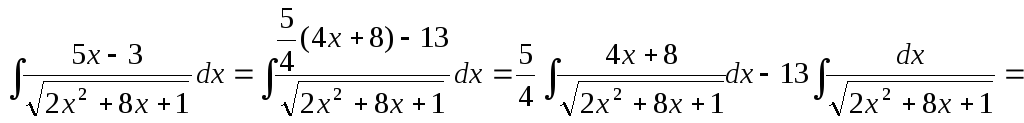
Таким образом, к первому типу можно отнести следующие подынтегральные выражения, представленные в таблице 5.

Таблица 5.

№	подынтегральное выражение	преобразования	замена	dx
1.
2.
3.
4.			,
5.	, где

• Ко второму типу относят интегралы вида , гдеP_n(x) – многочлен п-ой степени. Интеграл находится с помощью тождества, называемое методом неопределённых коэффициентов:

=,

где Q_n-1(x) – многочлен степени равной п-1 с неопределёнными коэффициентами, λ – некоторый неопределённый коэффициент.

Примеры:

а)

Здесь n = 3, поэтому соответствующее тождество имеет вид:

.

Продифференцируем полученное выражение:

Умножим на и сгруппируем коэффициенты при одинаковых степенях х:

=

=

Итого =

=

b)

Здесь n = 4, поэтому соответствующее тождество имеет вид:

Дифференцируем полученное выражение:

Перегруппировываем:

• К третьему типу относят интегралы вида .

Интегрируются с помощью тригонометрической подстановки, которая называются подстановкой Эйлера. При необходимости выделяют под радикалом полный квадрат, т.е. , и вводят обозначение:,.

Примеры:

a)

b)

с)

Таким образом, введя новые обозначения имеем следующие подынтегральные выражения, которые будут иметь соответствующие тригонометрические подстановки, представленные в таблице 6.

№	подынтегральное выражение	замена	dt
1		или	или
2		или	или
3		или	или

Таблица 6.

• Четвёртый тип ,где m, n, и p – рациональные числа, называют интегралами от дифференциального бинома.

Академиком Чебышевым П.Л.¹ было доказано, что интеграл от дифференциального бинома может быть выражен через элементарные функции только в следующих трех случаях: Таблица 7.

№	случаи	замена
1	р – целое число	или , где -общий знаменатель m и n.
2	–целое число	подстановкой , где s – знаменатель числа р.
3	- целое число	, где s – знаменатель числа р.

Примеры:

a)

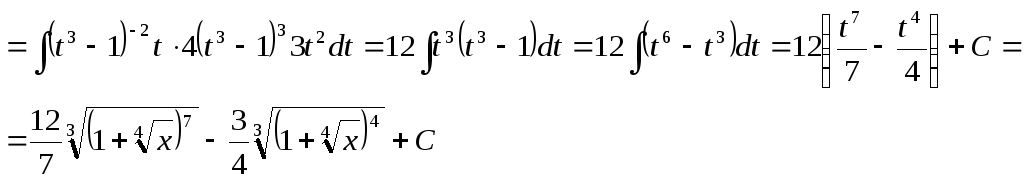
b)