Логический уровень.

Модели дискретных каналов передачи.

Н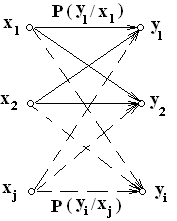а логическом уровне может быть построена модель дискретного канала, которая отражает процесс передачи элементов кода по этому каналу. В общем случае дискретный канал имеет на входе множество символов кодаХс энтропией источникаН(Х), а на выходе множество символовY с энтропиейH(Y). Модель такого канала можно изобразить в виде графа, в узлах которого расположены символы кода, а дуги отображают вероятности перехода из одного символа в другой. Количество символов конечно и определяется основанием системы счисления кода на входе канала. Вероятности переходов могут быть записаны в виде матрицы. Элемент матрицыP(y_i/x_j)определяет появление на выходе символаy_iпри подаче на вход символаx_j.

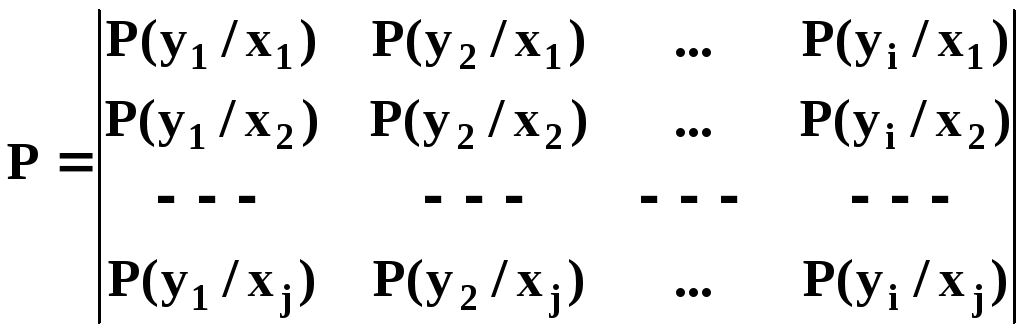
Вероятности, связывающие символы с одинаковыми индексами, называются вероятностями прохождения, остальные –вероятности трансформации.

Для определенных соотношений между вероятностями, входящими в данную матрицу можно выделить симметричныеканалы, у которых элементы, входящие в строки и столбцы, являются перестановками одних и тех же чисел.

По основанию системы счисления кода на входе канала различают двоичные, десятичные и другие каналы.

Пропускная способность канала на логическом уровне определяется количеством бит на один символ (знак) и не связана со временем. Количество информации, передаваемое одним символом, составит

I_max= H_max(Y) – H_min(Y/X).

Если n– количество символов на входе канала,m– количество символов на выходе канала, слагаемые можно подсчитать так.

Максимальная энтропия выходного сигнала:

, где

Энтропия шумов:

Конкретные типы дискретных каналов.

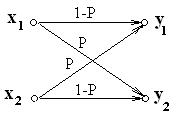
Двоичный симметричный канал с шумом.

При наличии шума (помех) в канале передачи входной символ x_jпереходит в символy_iс вероятностьюP(y_i/x_j). Обозначим вероятность искажения символаР

Вероятность его прохождения будет равна P(y_i/x_j)приi = j, что для двоичного канала составит1 – Р.

Граф симметричного двоичного канала, и матрица вероятностей будут иметь вид.

Количество информации, передаваемое одним символом по такому каналу, составит при равновероятных входных символах I_max= 1 – H_min(Y/X), т.к. выше было показано, что в этом случаеH_max(Y) = 1.

Находим условную энтропию:

H(Y/X) = -(1-P)log₂(1-P)-Plog₂P

Следовательно:

I = 1 + (1-P)log₂(1-P) + Plog₂P

Если P(x₁)  P(x₂),тоH_max(Y) вычисляется по общей формуле

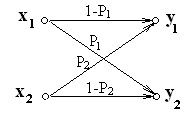
Несимметричный двоичный канал с шумом

Здесь вероятность искажения символа x₁равнаР₁, а вероятность искажения символаx₂равнаР₂.

Граф несимметричного двоичного канала, и матрица вероятностей будут иметь вид.

Количество информации, передаваемое символом по каналу:

I = H (Y) – H (Y/X)

При этом максимальная энтропия в выходных сигналах рассчитывается по формуле полной энтропии: H(Y) = -Р(у₁)log₂Р(у₁) - Р(у₂)log₂Р(у₂)

Энтропия шумов вычисляется по формуле условной энтропии:

H(Y/Х) = -Р(х₁)[Р(у₁/х₁)log₂Р(у₁/х₁)+Р(у₂/х₁)log₂Р(у₂/х₁)] -

- Р(х₂)[Р(у₁/х₂)log₂Р(у₁/х₂) + Р(у₂/х₂)log₂Р(у₂/х₂)]

Двоичный канал передачи со стиранием.

Для уменьшения вероятности трансформации символов в каналах с помехами (шумами), используют каналы со стиранием. В таких каналах в приемном устройстве существует специальная зона стирания, при попадании в которую формируется символ стирания. Не следует думать, что при попадании в зону стирания входной символ пропадает совсем. В данном случае вместо трансформированного (ошибочного) символа вырабатывается новый символ – символ неопределенности. Во многих случаях это позволяет легче исправить искажения информации. На выходе двоичного канала со стиранием будут присутствовать уже не два, а три символа.

О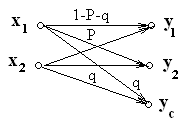бозначим вероятность стирания символаq, и рассмотрим граф канала со стиранием и соответствующую матрицу вероятностей.

Найдем количество информации, передаваемое одним символом по такому каналу. При наличии символов стирания понятие равновероятности символов на выходе канала не имеет смысла, поэтому энтропия на выходе канала определится так:

где P(y_i)– вероятность возникновения на выходе канала символаy_i.

Для равновероятных символов на входе канала и одинаковой вероятности их искажения Римеют место следующие соотношения.

Р(х₁) = Р(х₂) = 1/2

Р(у₁) = Р(х₁)Р(у₁/х₁) + Р(х₂)Р(у₁/х₂) = (1-Р-q)/2 + Р/2 = (1-q)/2

Р(у₂) = Р(у₁)

Р(у_С) = Р(х₁)Р(у_С/х₁) + Р(х₂)Р(у_С/х₂) = q/2 + q/2 = q

Отсюда

H(Y) = (1-q)[1-log₂(1-q)]-qlog₂q

Соответственно условная энтропия в общем виде:

Или для рассматриваемого канала:

H(Y/Х) = -(1-Р-q)log₂(1-P-q) + Рlog₂Р + qlog₂q

Отсюда количество информации, передаваемое одним символом по каналу со стиранием при равновероятных входных сигналах и одинаковой вероятности их искажения:

I = (1-q)[1-log₂(1-q)] + (1-Р-q)log₂(1-P-q) + Рlog₂Р