
- •Глава 1. Предмет и задачи метрологии
- •1.1. Предмет метрологии
- •1.2. Структура теоретической метрологии
- •3.3. Международная система единиц (система си)
- •3.4. Воспроизведение единиц физических величин и передача их размеров
- •3.4.1. Понятие о единстве измерений
- •3.4.2. Эталоны, единиц физических величин
- •3.4.3. Поверочные схемы
- •Глава 4. Основные понятия теории погрешностей
- •4.1. Классификация погрешностей
- •4.2. Принципы оценивания погрешностей
- •4.5. Правила округления результатов измерений
- •Глава 5. Систематические погрешности
- •5.1. Систематические погрешности и их классификация
- •5.2. Способы обнаружения и устранения систематических погрешностей
- •Глава 6. Случайные погрешности
- •6.1. Вероятностное описание случайных погрешностей
- •6.3. Основные законы распределения
- •6.3.1. Общие сведения
- •6.3.2. Трапецеидальные распределения
- •6.3.3. Экспоненциальные распределения
- •6.3.4. Нормальное распределение (распределение Гаусса)
- •6.3.6. Семейство распределений Стъюдента
- •Глава 7. Грубые погрешности и методы их исключения
- •7.1. Понятие о грубых погрешностях
- •7.2. Критерии исключения грубых погрешностей
- •Глава 8. Обработка результатов измерений
- •8.1. Прямые многократные измерения
- •8.1.1. Равноточные измерения
- •8.2. Однократные измерения
- •8.3. Косвенные измерения
- •Глава 9. Суммирование погрешностей
- •9.1. Основы теории суммирования погрешностей
- •9.2. Суммирование систематических погрешностей
- •9.3. Суммирование случайных погрешностей
- •9.4. Суммирование систематических и случайных погрешностей
- •9.5. Критерий ничтожно малой погрешности
- •Глава 11. Средства измерений
- •11.1. Понятие о средстве измерений
- •11.2. Статические характеристики и параметры средств измерений
- •11.3. Динамические характеристики и параметры средств измерений
- •11.4.Классификация средств измерений
- •11.5. Элементарные средства измерений
- •11.6. Комплексные средства измерений
- •11.6.1. Измерительные приборы и установки
- •11.6.2. Измерительные системы и измерительно-вычислительные комплексы
- •11.7. Моделирование средств измерений
- •11.7.1. Структурные элементы и схемы средств измерений
- •11.7.2.Структурная схема прямого преобразования
- •11.7.3.Уравновешивающее преобразование
- •11.7.4. Расчет измерительных каналов средств измерений
- •Глава 12. Метрологические
- •12.2. Метрологические характеристики, предназначенные для определения результатов измерений
- •12.3. Метрологические характеристики погрешностей средств измерений
- •12.4. Характеристики чувствительности средств
- •Измерений к влияющим величинам.
- •Неинформативные параметры выходного
- •Сигнала
- •12.5. Нормирование динамических характеристик средств измерений
- •12.6. Метрологические характеристики влияния на инструментальную составляющую погрешности измерения
- •12.7. Комплексы нормируемых метрологических характеристик средств измерений
- •12.8. Расчет погрешностей средств измерений по нормированным метрологическим характеристикам
- •12.9.Классы точности средств измерений
- •Глава 13. Метрологическая надежность средств измерений
- •13.1. Основные понятия теории метрологической надежности
- •13.2. Изменение метрологических характеристик средств измерений в процессе эксплуатации
- •13.5. Метрологическая надежность и межповерочные интервалы
- •Приложение 1. Статистические таблицы
- •Глава 1. Предмет и задачи метрологии 1
- •Глава 12. Метрологические 100
- •Глава 13. Метрологическая надежность средств измерений 126
9.2. Суммирование систематических погрешностей
При определении границ систематическая погрешность оценивается по ее составляющим, называемым элементарными систематическими погрешностями. Если для части составляющих находят их оценки и эти погрешности устраняют введением поправок, то в качестве рассматриваемых элементарных погрешностей выступают погрешности определения поправок, которые также характеризуются границами.
При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых:
9.3. Суммирование случайных погрешностей
Правила суммирования случайных погрешностей основаны на известных из теории вероятностей положениях:
а) оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих;
б) оценка СКО суммарной погрешности определяется выражением
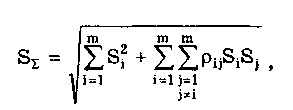 (9.7)
(9.7)
где Si — оценка СКО i-й составляющей погрешности; m — число суммируемых составляющих погрешностей; ρij — коэффициент корреляции между i- и j-й составляющими.
9.4. Суммирование систематических и случайных погрешностей
При проведении многократных измерений случайная погрешность может быть уменьшена во много раз. Однако погрешность усредненного результата будет определяться не этой весьма малой случайной погрешностью, а не зависящей от числа усредняющих отсчетов систематической погрешностью.
Механизм суммирования систематической и случайной составляющих погрешности отличается от механизма суммирования случайных погрешностей. Согласно ГОСТ 8.207—76 погрешность результата измерения определяется по следующим правилам. Если границы неисключенной систематической погрешности 6 и оценка СКО результата измерения S связаны соотношением
![]() (9.16)
(9.16)
то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. При этом доверительные границы погрешности результата = tpS, где tp — коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа проведенных измерений п. Если же имеет место неравенство
![]() (9.17)
(9.17)
то, наоборот, следует пренебречь случайной составляющей и результат характеризовать лишь границами его суммарной систематической погрешности = . Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности, при выполнении указанных неравенств не превышает 15%.
9.5. Критерий ничтожно малой погрешности
Вопрос о том, какими составляющими при расчете погрешностей можно пренебрегать, возникает постоянно. Это связано с тем, что степень точности определения суммируемых погрешностей невысока, поэтому нет смысла суммировать те из них, которые имеют по сравнению с другими малые значения, "поскольку это не повысит точности суммарной погрешности. Пренебрежение малыми погрешностями позволит упростить вычисления при нахождении результирующей погрешности. Следовательно, необходимо установить критерий ничтожно малой погрешности, т.е. математическое правило, позволяющее исключать последнюю из расчета. Этот критерий также необходим при выборе класса точности образцового средства измерений в зависимости от класса точности поверяемого средства измерений.
Один из возможных вариантов определения критерия ничтожно малой погрешности состоит в том, что если одна величина больше другой на порядок, то ею можно пренебречь.
При сложении некоррелированных случайных составляющих суммируются их дисперсии (СКО). В случае двух составляющих суммарная случайная погрешность определяется по формуле

где (1), (2) — СКО первой и второй составляющих.
В соответствии с критерием, если дисперсия первой составляющей 2(1), больше дисперсии второй составляющей 2(2), более чем в 10 раз, то СКО (), суммарной случайной погрешности составит 1,05(1). Следовательно, пренебрежение дисперсией второй составляющей по сравнению с дисперсией первой составляющей приводит к тому, что СКО суммарной случайной погрешности будет определено с ошибкой в 5%. Критерий ничтожно малой погрешности для СКО случайной погрешности запишется в виде (1) > 10̅(2) 3(2). Таким образом, погрешностью можно пренебречь, если ее СКО или доверительный интервал в 3 раза меньше, чем у оставляемых погрешностей.
Контрольные вопросы
1. На чем основана теория расчетного суммирования погрешностей?
2. Как могут быть определены квантильные множители суммарной погрешности результата измерения?
3. Сформулируйте правила, по которым суммируются систематические погрешности.
4. Расшифруйте понятия коррелированных и некоррелированных случайных величин. Что считается границей между этими случайными величинами при их суммировании?
5. Каким образом суммируются коррелированные случайные величины?
6. По каким правилам суммируются некоррелированные случайные величины?
7. Как суммируются случайные и систематические погрешности? Какой нормативный документ регламентирует эти правила?
8. В чем состоит суть критерия ничтожно малой погрешности?
