1. Свойство коммутативности:

а) (AB) ~ (BA)

б) (AB) ~ (BA)

2. Ассоциативный закон:

а) [A (BC)] ~ [(AB) C]

б) [A (BC)] ~ [(AB) C]

3. Дистрибутивный:

а) [A (BC)] ~ [(AB)  (AC)]

б) [A (BC)] ~ [(AB)  (AC)]

4. Идемпотентность:

AA ~ A

AA ~ A

5. ¬Л ~ И

¬И ~ Л

6. АИ ~ И

АИ ~ А

7. АЛ ~ А

АИ ~ А

8. Законы Аристотеля:

а) А ~ И - 1-ый закон (закон исключенного третьего),

б) А ~ Л - 2-ой закон (закон противоречия)

9. Закон элиминации:

а) A (AB) ~ A

б) A (AB) ~ A

10.Закон де Моргана:

а) ~

б) ~

11. Закон двойного отрицания

() ~A

12. (A→B) ~ (B)

Теорема 3. (О замене эквивалентных формул).

Пусть С_­А­ – формула, содержащая в качестве составной части некоторую формулу А. Формула С_­В­­_­­­­­_­­_­­ получена из формулы С_­А­ путем замены А на В. ­

С_­А­ и С_­В­ - посылки. Тогда, если А ~ В, то ­С_­А­ ~ С_­В­.

Доказательство: A~B, это означает, что в таблице истинности относительно знака эквиваленции мы имеем одинаковые значения, следовательно, в исходной формуле С­­­­_­­А мы можем заменить А на эквивалентное В. Следовательно, полученное значение C_В будет эквивалентно С_А.

правило 12 (т.2)

Рассмотрим пример:

~

~~

~~~~

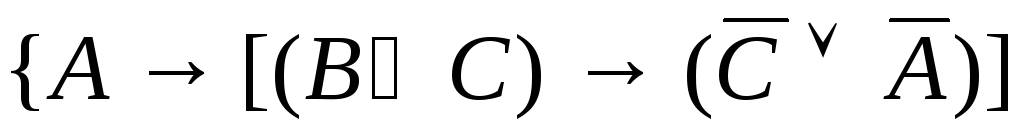
пр.2 пр.4б пр.10а пр.9а

Законы теоремы 2 совпадают с законами алгебры Буля.

ą_Буля = {{a, b, c, …; 0, 1};+,-,=}

^{перемен. пост. операции}

_­­­­­­

Свойства алгебры Буля.

1. a·b=b·a

a+b=b+a

2. a·(b·c)=a·b·с

a+(b+c)=(a+b)+c=a+b+c

3. a+(b·c)=(a+b)·(a+c) дистрибутивность

a·(b+c)=(a·b)+(a·c)

4. a·a=a 7. =·

a+a=a =+

5. a·ā=0 8. a·1=a

a+ā=1 a+0=a

6. a+(a·b)=a 9. =1

a·(a+b)=a =0

Классы формул:

1. Тавтология: P(A, B, C, …) ≡ И (╞ p).

2. Тождественно ложные: P(A, B, C, …) ≡ Л

3. Выполнимые: P(A, B, C, …)

Теорема 4. Если╞A и ╞ (AB), то ╞В, т.е.[╞A & ╞(АВ)]  ╞B.

Доказательство:

Пусть 1) А.

2) АВ. посылки.

Тогда при истинности посылок (А и АВ) по свойству импликации имеем, что заключение ╞В.

Теорема 5. При любых значениях логических переменных А, В, С выполняются тождества:

1. А(ВА) ≡ И

2. ((АВ)  ((А(ВС))  (АС))) ≡ И

2.1. ((АВ)  А) ≡ И

2.2. ((АВ)  В) ≡ И

2.3. (А(В(АВ))) ≡ И

3.1. (А(АВ)) ≡ И

3.2. (В(АВ)) ≡ И

3.3. ((АС)  ((ВС)  ((АС)  С))) ≡ И

4.1. ((АВ)  ((А¬В)  ¬А)) ≡ И

4.2. (А) ≡ И

	А		B		C		AC		BC		AC			(AC) C
	И		И		И		И		И		И			И
	И		И		Л		Л		Л		И			Л
	И		Л		И		И		И		И			И
	И		Л		Л		Л		И		И			Л
	Л		И		И		И		И		И			И
	Л		И		Л		И		Л		Л			И
	Л		Л		И		И		И		И			И
	Л		Л		Л		И		И		Л			И

A	B	С	(BC) ((AC)C	AB	((AB) ((A(BC))(AC)))
И	И	И	И	И	И
И	И	Л	И	И	И
И	Л	И	И	Л	И
И	Л	Л	Л	Л	И
Л	И	И	И	И	И
Л	И	Л	И	И	И
Л	Л	И	И	И	И
Л	Л	Л	И	И	И

Доказательство: (с помощью соответствующей таблицы истинности)

A	B	BA	A( BA)	AB	A(AB)A	B(AB)	A&B
И	И	И	И	И	И	И	И
И	Л	И	И	И	И	И	Л
Л	И	Л	И	И	И	И	Л
Л	Л	И	И	Л	И	И	Л

A	B	A	B	A&B	A&BA	A(B((A&B)
И	И	И	И	И	И	И
И	Л	И	Л	Л	И	И
Л	И	Л	И	Л	И	И
Л	Л	Л	Л	Л	И	И

A	B	A	B	AB *	A	(A)**	*  **
И	И	И	И	И	Л	И	И
И	Л	И	Л	Л	И	Л	И
Л	И	Л	И	И	И	И	И
Л	Л	Л	Л	И	И	И	И