ПРИЛОЖЕНИЕ 2. СХОДИМОСТЬ МЕТОДА ГАЛЕРКИНА
Основные понятия и определения1
Последовательность {xn } X называется фундаментальной, еслиε > 0 N = N(ε), что n > N и любых натуральных p выполняется неравенство 
 xn+ p − xn
xn+ p − xn 
 < ε.
< ε.
Нормированное пространство X вложено в нормированное пространст-
во |
ˆ |
если всюду на X задана линейная функция J(x) со значениями в |
ˆ |
при- |
X , |
X , |
чем существует постоянная β > 0 такая, что |
|
|
|
|
|
|
|
J (x) |
|
|
|
ˆ ≤β |
|
|
|
x |
|
|
|
x X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
|
Прямой суммой Z = X + Y двух линейных пространств X и Y называется совокупность пар z = (x, y), для которых операции сложения пар и умножения пары на число определяются следующим образом: если z1 = (x1, y1), z2 = (x2, y2) и α1, α2 – скаляры, то
α1z1 + α2 z2 = (α1x1 + α2 x2 , α1 y1 + α2 y2 ).
Линейное многообразие L, лежащее в нормированном пространстве E (L E), называется плотным в E, если x E, ε > 0 найдется элемент u L
такой, что 
 x − u
x − u
 < ε.
< ε.
Нормированное пространство называется полным, если в нем всякая фундаментальная последовательность сходится. Полное нормированное пространство называется банаховым.
Пусть X – банахово пространство, а R – вещественная ось, L(X , R) – банахово пространство линейных ограниченных функционалов, заданных на X. Это
|
|
|
пространство называется сопряженным к X и обозначается |
X * = L(X , R). Зна- |
чение линейного функционала f X * на x X обозначается |
x, f . |
Последовательность |
{xn } X называется слабо сходящейся к элементу |
x X , если xn , f → x, f |
f X * . Если xn → x слабо, то x называется сла- |
бым пределом {xn }. В отличие от слабо сходящихся последовательности, схо-
дящиеся по норме пространства X, называются сильно сходящимися.
1 Основные понятия и определения вводятся в соответствии с [41].
401

Множество M банахова пространства X называется слабо компактным, если из любой (бесконечной) последовательности его элементов можно выбрать слабо фундаментальную (в смысле слабой сходимости) последовательность.
Нормированное пространство X называется сепарабельным, если в нем существует счетное множество, плотное в X.
Пространство H со скалярным произведением называется гильбертовым, если оно полно в смысле сходимости по норме, порожденной скалярным произведением.
Пусть в гильбертовом пространстве H задано подпространство M. Согласно теореме Рисса1 каждому x H можно поставить в соответствие единственный элемент y M – ортогональную проекцию x на M. Тем самым в H опреде-
лен оператор ортогонального проектирования (для краткости – проектор) y = Px.
~1
Пространство H[a,b] состоит из всевозможных функций u(x), непрерывно
дифференцируемых (верхний индекс возле символа Н показывает, сколько именно раз дифференцируемы функции) на [a, b], со скалярным произведением
(u,v)= ∫b u(x)v(x)dx + ∫b u′(x)v′(x)dx
инормой, соответствующей этому скалярному произведению,
1Рисс Фридьеш [22.1.1880 – 28.2.1956] – венгерский математик. Учился в Цюри-
хе (1897 – 1899), Будапеште (1899 – 1901), Геттингене и Париже (1903 – 1904). В 1916 году стал членом Венгерской академии наук. Профессор университетов в Клуже (1912 – 1919), Сегеде (1920 – 1945), Будапеште (с 1946). Основные труды опубликовал по функциональному анализу. Изучал векторные пространства, исследовал системы линейных уравнений с бесконечным числом неизвестных, один из основателей теории топологических пространств.
Теорема Ф. Рисса [41]: пусть H – гильбертово пространство. Для любого линейного ограниченного функционала f, заданного повсюду на H, существует единственный элемент
y H такой, что x H x, f = x, y , при этом
, при этом 
 f
f 
 =
= 
 y
y
 .
.

|
|
|
b |
|
b |
1 2 |
|
|
|
|
u |
= ∫u2 |
(x)dx + ∫u′2 |
(x)dx . |
|
|
|
|
|
a |
~1 |
a |
|
|
|
1 |
является пополнением |
в этой норме. Элементами |
1 |
явля- |
H(a,b) |
H[a,b] |
H(a,b) |
ются классы, состоящие из последовательностей { m } ~[1a,b], фундаментальных u H
~1
вH[a,b] в среднем, то есть таких, что
|
b |
[u |
m |
(x) − u |
n |
(x)]2 dx + b |
[u′ |
(x)− u′ |
(x)]2 dx →0. |
|
∫ |
|
|
∫ |
m |
n |
|
m,n→∞ |
|
|
a |
|
|
|
|
a |
|
|
|
~1 |
|
|
Из условия фундаментальности {um } в среднем в |
следует, что по от- |
|
H[a,b] |
дельности
b
∫[um (x)− un (x)]2 dx →0,
m,n→∞
a
b
∫[um′ (x)− un′ (x)]2 dx →0.
m,n→∞
a
Согласно определению [41] пространства L2 (a,b) существуют функции u(x) L2 (a,b) и w(x) L2 (a,b) такие, что
u |
m |
(x) →u(x), |
u′ (x) →w(x) |
|
|
|
|
m→∞ |
m |
m→∞ |
|
|
|
|
|
~1 |
(a,b) определены элемент u с предста- |
в среднем. Пусть {um } H(a,b) , тогда в L2 |
|
|
|
|
′ |
}. Элемент w называется обоб- |
вителем {um } и элемент w с представителем {um |
щенной производной (в смысле Соболева) от u. |
|
|
|
|
|
|
|
|
|
|
|
Пространство H(1a,b) |
является пополнением в метрике |
|
|
|
u |
|
|
|
2 1 |
(a,b) |
= ∫b u′2 (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
a |
линейного пространства непрерывно дифференцируемых функций, прини-
мающих на границе значения, равные нулю. H(1a,b) является гильбертовым про-
b |
|
странством со скалярным произведением (u,v)= ∫u′(x)v′(x)dx. |
|
a |
|
Обобщенное решение дифференциального уравнения |
|
Рассматривается уравнение |
|
Ax = y, |
(П2.1) |

где A – линейный оператор, действующий из плотной в вещественном гильбертовом пространстве X области определения D(A) в то же самое пространство X. Скалярное произведение в X обозначается через (x, y), а соответствующая ему норма – через 
 x
x
 . H – еще одно гильбертово пространство со скалярным произ-
. H – еще одно гильбертово пространство со скалярным произ-
ведением [x, y] и нормой ||| x ||| , соответствующей этому скалярному произведению. Пусть выполнены следующие условия:
1. H вложено в X, H D(A), причем в H + H определен билинейный ограниченный функционал a(u, v), то есть вещественнозначная функция, линейная по u при фиксированном v, линейная по v при фиксированном u, такая, что
|
a(u,v) |
|
≤ c ||| u ||| ||| v ||| , |
(П2.2) |
|
|
при этом x D(A) и v H |
|
|
a(x,v)≡ (Ax,v). |
(П2.3) |
2. Существует константа γ > 0 такая, что u H выполняется неравенство |
|
a(u,v)≥ γ ||| u |||2 . |
(П2.4) |
Оператор, удовлетворяющий условиям 1 и 2, называется H-эллиптическим. x H – обобщенное решение уравнения (П2.1) с H-эллиптическим оператором A,
если имеет место тождество |
|
a(x,v)= (y,v). |
(П2.5) |
В H выбирается координатная система ϕi , i =1,∞. Пусть Pm – проектор H на линейное подпространство Hm, натянутое на первые m векторов этой систе-
мы. Элемент xm Hm |
называется галеркинским приближением обобщенного |
решения уравнения (П2.1), если vm Hm имеет место тождество |
|
|
|
a(xm ,vm )= (y,vm ). |
(П2.6) |
Лемма П2.1. Решение задачи (П2.6) имеет вид |
|
|
|
|
m |
|
|
|
xm = ∑biϕi , |
(П2.7) |
|
|
|
i=1 |
|
где коэффициенты bi , |
i = |
|
определяются решением системы m линейных |
1,m |
уравнений с m неизвестными, |
|
∑m |
a(ϕi ,ϕj )bi = (y,ϕj ), j = |
|
. |
(П2.8) |
1,m |
i=1 |
|
|
|
|
|
|
Доказательство. Элемент xm принадлежит Hm и, значит, имеет вид (П2.7). При подстановке в (П2.6) представления (П2.7) и выражения
j=1
всилу билинейности a(u, v) и линейности скалярного произведения получается
|
|
|
|
|
|
∑m |
a(ϕi ,ϕj )bic j = ∑m (y,ϕj )c j . |
(П2.10) |
i, j=1 |
j=1 |
|
Но vm Hm произвольно, то есть c j , j = |
|
|
в (П2.9) и (П2.10) – произ- |
1,m |
вольные постоянные. Следовательно, (П2.6) и (П2.10) эквивалентны. Что и требовалось доказать.
Лемма П2.2. Пусть оператор A является H-эллиптичным. Тогда для всякого m существует единственное галеркинское приближение xm обобщенного решения уравнения (П2.1).
Доказательство. Если a(xm ,vm )= 0 vm Hm , то это верно и при vm = xm . Но тогда в соответствии с (П2.4) условия 2
0 = a(xm , xm )≥ γ ||| xm |||2 ,
откуда следует, что xm = 0. Поскольку однородная задача, получающаяся из (П2.6) при y = 0, имеет лишь тривиальное решение, то задача (П2.8), а вместе с ней и (П2.6), будут однозначно разрешимы. Что и требовалось доказать.
|
|
Лемма П2.3. Если |
u |
m |
→u |
0 |
слабо в H, а v |
m |
→v |
0 |
сильно в H, то |
a(u |
|
|
|
) →a(u |
|
|
|
|
|
|
m→∞ |
|
|
|
m→∞ |
|
m |
,v |
m |
0 |
,v |
0 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Вследствие билинейности |
|
|
|
|
|
|
|
|
a(um ,vm )− a(u0 ,v0 )= a(um ,vm − v0 ) + a(um − u0 ,v0 ). |
|
(П2.11) |
|
|
Так как последовательность {um } |
сходится слабо, то согласно [41] она ог- |
раничена. Поэтому из неравенства (П2.2) следует |
|
|
|
|
|
|
|
|
|
a(u |
|
,v |
|
− v |
) |
|
≤ c ||| u |
|
||| ||| v |
− v ||| →0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
0 |
|
|
|
m |
m |
0 |
|
m→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку v0 фиксировано, u H выражение a(u,v0 ) определяет в H линейный ограниченный функционал. Но тогда, по теореме Рисса, найдется элемент w0 H такой, что a(u,v0 ) = [u, w0 ] u H. Согласно определению слабой сходимости {um } к u0, имеет место

a(um −u0 ,v0 )= [um − u0 , w0 ] →0.
m→∞
В(П2.11) оба слагаемых в правой части равенства стремятся к нулю, что
идоказывает утверждение леммы.
Теорема П2.1. Пусть пространство H сепарабельно и оператор A является H-эллиптичным, тогда:
1) для всякого m галеркинское приближение xm обобщенного решения уравнения (П2.1) существует и единственно;
2) обобщенное решение уравнения (П2.1) существует и единственно;
3) x |
m |
→x |
0 |
слабо; при этом справедлива оценка |
|
|
m→∞ |
|
|
|
|
|
|
|
|
|
|
||| x |
m |
− x |
0 |
|||≤ cγ−1 ||| P x − x |||. |
(П2.12) |
|
|
|
|
|
|
m |
|
Доказательство. Утверждение 1) теоремы верно в силу леммы П2.2. Для доказательства утверждения 2) используется сепарабельность пространства H. Пусть, как и ранее, ϕi , i =1,∞ – ортонормированный базис в H. v H
Pmv →v , то есть ряд Фурье, построенный для элемента v, сходится к v.
m→∞
Рассматривается последовательность галеркинских приближений {xm }. Полагая
в (П2.6) |
|
vm = xm и пользуясь неравенством (П2.4), можно получить |
|
|
|
|
|
|
|
|
γ ||| xm |||2 ≤ a(xm , xm )= (y, xm )≤ |
|
|
|
y |
|
|
|
|
|
|
|
xm |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Но H вложено в X, и поскольку xm H , то найдется постоянная k > 0 та- |
кая, что |
|
|
|
xm |
|
|
|
≤ k ||| xm ||| при m = 1, 2, … . Следовательно, |
|
|
|
|
γ ||| xm |||2 ≤ k ||| xm |||
 y
y
 ,
,
откуда
||| xm |||≤ kγ−1 
 y
y
 .
.
Значит, последовательность галеркинских приближений {xm } ограничена в H, и тогда она слабокомпактна. Пусть {xm′} – ее подпоследовательность, сходящаяся в H слабо к некоторому элементу x0 H. Если зафиксировать произ-
вольный |
элемент v H, то |
в |
соответствии с (П2.6) |
получается, что |
a(x |
′, P |
′v)= (y, P |
′v). При этом |
P |
′v →v |
сильно, а |
x |
′ →x |
0 |
слабо. |
m |
m |
|
m |
|
m |
′ |
|
m |
′ |
|
|
|
|
|
|
|
m →∞ |
|
|
m →∞ |
|
|
По лемме П2.3 и свойству непрерывности скалярного произведения имеет место a(x0 ,v)= (y,v). Из произвольности v H следует, что x0 – обобщенное решение уравнения (П2.1).
Пусть x0 , x0′ – два обобщенных решения. Для произвольного v H a(x0 ,v) = (y,v), a(x0′,v)= (y,v).
Вычитание второго тождества из первого дает выражение a(x0 − x0′,v)= 0. Полагая v = x0 − x0′ и используя (П2.4), можно получить
|
0 = a(x0 − x0′, x0 − x0′ )≥ γ ||| x0 − x0′ |||2 , |
|
и, следовательно, |
x0 = x0′. Подстановка в (П2.5) v = vm |
и вычитание его из |
(П2.6) дает |
a(xm − x,vm )= 0 vm Hm . |
|
|
|
В частности, |
a(xm − x, xm )= a(xm − x, Pm x) = 0. Но тогда по условию 2 |
γ ||| xm − x |||2 ≤ a(xm − x, xm − x) = −a(xm − x, x)= |
|
= a(xm − x, Pm x − x)≤ c ||| xm − x |||||| Pm x − x ||| . |
Отсюда следует оценка (П2.12). Что и требовалось доказать. |
Сходимость метода конечных элементов |
|
Рассматривается дифференциальное уравнение |
|
|
− (g(t)x′)′ + c(t)x = y(t) |
(П2.13) |
с граничными условиями |
|
|
x(0) = 0, x(1) = 0. |
(П2.14) |
Коэффициент g(t) считается непрерывно дифференцируемым на [0, 1], а коэффициенты c(t) и y(t) – непрерывными на [0, 1]. Пусть на отрезке [0, 1]
g(t)≥ α > 0, c(t)≥ β > 0. |
(П2.15) |
Функция x(t) H(10,1), удовлетворяющая для всех v(t) H(10,1) |
тождест- |
ву (П2.5), называется обобщенным решением задачи (П2.13)–(П2.14), где в данном случае
a(x,v)≡ ∫1 g(t)x′(t)v′(t)dt + ∫1 c(t)x(t)v(t)dt ,
1
(y,v) ≡ ∫ y(t)v(t)dt.
0
Тождество (П2.5) получается в результате скалярного умножения в L2 (0,1)
уравнения (П2.13) на произвольную функцию v(t) H(10,1) и интегрирования по
частям. Это позволяет понизить требования гладкости к функции x(t), одновременно повысив требования дифференцируемости функции v(t). В качестве ко-
ординатной системы в Hm H(10,1) выбирается система функций (рис. П2.1)
|
|
|
ϕ0 |
1 − mt, t [0, 1 m], |
|
|
|
(t)= |
|
|
|
|
0, t [1 m, 1]; |
|
|
|
|
|
|
|
1 − i + mt, t [(i − 1) m, i m], |
|
|
|
|
|
|
|
ϕ |
(t)= |
|
+ i |
− mt, t [i m, (i + 1) m], |
1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
t [(i −1) m, (i + 1) m], i = 1,m − 1; |
|
|
|
|
|
|
|
|
|
|
|
0, t [0, 1 −1 m], |
|
ϕm (t) = |
|
|
|
|
m −1 + mt, t [1 − 1 m, 1]. |
|
|
|
|
|
Рис. П2.1. Вид функции ϕi координатной системы
в Hm H(10,1)
Для задачи (П2.13)–(П2.14) показано [41], что ее обобщенное решение
в действительности принадлежит C[20,1] . Там же получена оценка, показывающая, что для всякой функции x(t) H(20,1) при m → ∞

 x − Pm x
x − Pm x
 H(10,1) = O(1
H(10,1) = O(1 m),
m),
где Pm – проектор в H(10,1) на подпространство кусочно-линейных функций, натянутое на ϕi , i =1,m . Таким образом, из оценки теоремы П2.1 следует сходимость галеркинских аппроксимаций xm к точному решению задачи.
ПРИЛОЖЕНИЕ 3. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица П3.1 |
Тип уравнения |
|
|
|
|
Фундаментальное |
|
|
|
|
|
|
|
|
|
|
|
|
|
решение [4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одномерные уравнения, r = |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Лапласа |
|
′′ |
|
|
|
|
u = r 2 |
|
|
|
|
|
|
|
|
uxx + δ(x) = 0 |
|
|
|
|
|
|
|
Уравнение |
|
′′ |
|
|
|
|
u = −sin(λr) 2λ |
|
|
|
|
|
|
uxx + λ u + δ(x) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гельмгольца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Волновое уравнение |
|
2 |
|
′′ |
|
′′ |
u = −h(ct − r) 2λ |
|
|
|
|
|
c |
uxx − utt + δ(x)δ(t)= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение диффузии |
|
′′ |
|
−1 |
′ |
u = −h(t)e |
−r2 |
4kt |
|
4πkt |
|
|
uxx − k |
|
ux + δ(x)δ(t) = 0 |
|
|
|
Уравнение конвекции |
|
ut′ + vu′x + βu + δ(x)δ(t)= 0 |
u = −e−βr |
vδ(t − r v) |
(распада) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двумерные уравнения, r = |
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Лапласа |
|
′′ |
|
′′ |
+ δ(r) = 0 |
u = −ln(r) 2π |
|
|
|
|
|
uxx + uyy |
|
|
|
|
Уравнение |
|
u′′xx + u′′xx |
+ λ2u + δ(r)= 0 |
u = H0(2)(λr) |
4i |
|
|
|
|
Гельмгольца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
′′ |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
Уравнение Дарси |
|
|
|
|
u = − ln(x |
kx + y |
ky ) 4π kxky |
|
kxuxx + kyuyy + δ(r)= 0 |
|
|
(случай ортотропии) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Волновое уравнение c2 (u′xx′ + u′yy′ )− utt′′ + δ(r)δ(t)= 0 u = −h(ct − r)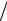 2πc(c2t 2 − r2 )
2πc(c2t 2 − r2 )
|
|
|
|
|
|
Уравнение |
utt′′ − μ2 |
u + δ(r)δ(t)= 0 |
|
u = h(t)Si(r 4μt) 2πμ |
для пластины |
|
|
|
|
|
|
|
|
|
|
Трехмерные уравнения, r = |
|
|
|
|
|
|
x2 + y2 |
+ z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Лапласа |
′′ |
′′ |
′′ |
|
|
u =1 2πr |
|
|
uxx + uyy + uzz + δ(r)= 0 |
|
|
|
Уравнение |
′′ |
′′ |
′′ |
2 |
|
u = e |
−iλr |
2πr |
Гельмгольца |
uxx + uyy + uzz + λ u + δ(r)= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
410



 xn+ p − xn
xn+ p − xn 
 < ε.
< ε.
 x − u
x − u
 < ε.
< ε.





 2πc(c2t 2 − r2 )
2πc(c2t 2 − r2 )
 , при этом
, при этом 


 =
= 


 .
.


 .
. 


 ,
,


 .
.
 x
x 

 m
m