xk, yk, zk |
ϕi (x, y)= αi + βi x + γi y + δi z |
xn, yn, zn |
z
Коэффициенты αi, βi, γi и δi определяются из системы уравнений
y
xj, yj, zj
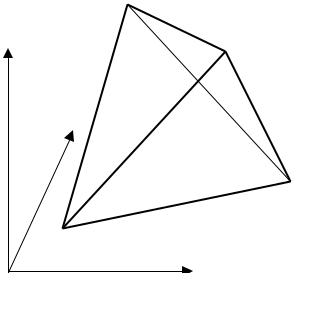
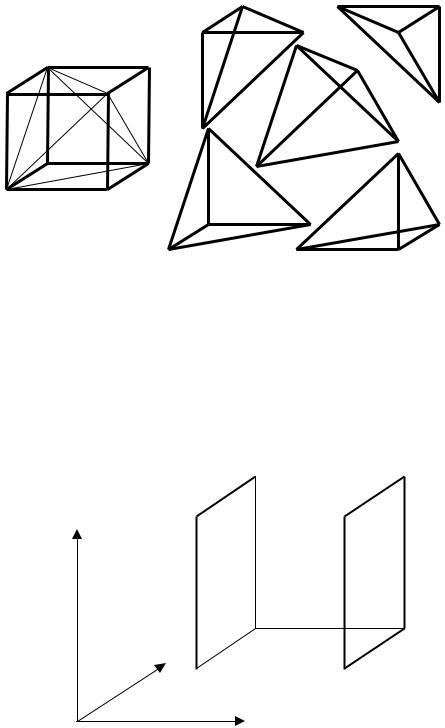
Рис. 13.15. Тетраэдральныйконечныйэлемент дляаппроксимациитрехмерныхтел
ϕi (xi , yi , zi )= αi + βi xi + γi yi + δi zi =1, |
|
|
(x |
|
, y |
|
, z |
|
)= α |
|
+ β |
x |
|
+ γ |
|
y |
|
+ δ |
z |
|
= 0, |
ϕ |
j |
j |
k |
i |
j |
i |
j |
j |
|
i |
|
|
|
|
i |
|
|
|
i |
|
|
ϕ |
(x |
k |
, y |
k |
, z |
k |
) = α |
i |
+ β |
x |
k |
+ γ |
i |
y |
k |
+ δ |
z |
k |
= 0, |
|
i |
|
|
|
|
i |
|
|
|
i |
|
|
|
|
(x |
|
, y |
|
, z |
|
) = α |
|
+ β |
x |
|
+ γ |
|
y |
|
+ δ |
z |
|
= 0. |
ϕ |
n |
n |
n |
i |
n |
i |
n |
n |
|
i |
|
|
|
|
i |
|
|
|
i |
|
|
Главный и вспомогательные определители этой системы уравнений соответственно равны
|
1 |
xi |
yi |
zi |
|
|
1 |
xi |
yi |
zi |
|
= |
1 |
x j |
y j |
z j |
, |
α = |
0 |
x j |
y j |
z j |
, |
|
1 |
xk |
yk |
zk |
|
|
0 |
xk |
yk |
zk |
|
|
1 |
xn |
yn |
zn |
|
|
0 |
xn |
yn |
zn |
|
|
1 |
1 |
yi |
zi |
|
|
1 |
xi |
1 |
zi |
|
β = |
1 |
0 |
y j |
z j |
, |
γ = |
1 |
x j |
0 |
z j |
, |
|
1 |
0 |
yk |
zk |
|
|
1 |
xk |
0 |
zk |
|
|
1 |
0 |
yn |
zn |
|
|
1 |
xn |
0 |
zn |
|
|
|
1 |
xi |
yi |
1 |
|
|
δ = |
1 |
x j |
y j |
0 |
. |
|
1 |
xk |
yk |
0 |
|
|
|
|
|
1 |
xn |
yn |
0 |
|
Искомые коэффициенты определяются выражениями
α = α  , β = β
, β = β 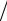 , γ = γ
, γ = γ  , δ = δ
, δ = δ 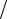 .
.
Следует отметить, что набором тетраэдральных конечных элементов могут быть представлены области в виде параллелепипедов (рис. 13.16).
311
а б
Рис. 13.16. Представление параллелепипеда (а) с помощью набора тетраэдральных конечных элементов (б)
В случае (рис. 13.17), когда конечный элемент является параллелепипедом со сторонами, параллельными координатным осям (hx, hy и hz – размеры сторон параллелепипеда), пробные функции определяются выражениями
|
|
xs, ys, zs |
|
xr, yr, zr |
z |
xp, yp, zp |
|
|
|
|
|
|
|
xq, yq, zq |
|
|
|
|
hz |
xn, yn, zn |
|
|
|
|
|
xk, yk, zk |
|
|
|
|
y |
|
hx |
|
hy |
xi, yi, zi |
|
xj, yj, zj |
x
Рис. 13.17. Конечный элемент а виде параллепипеда со сторонами, параллельными координатными осями
ϕi = −(x − x j )(y − yn )(z − zp )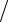 hx hy hz,
hx hy hz,
312
ϕj = (x − xi )(y − yn )(z − zp )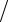 hx hy hz,
hx hy hz,
ϕk = −(x − xi )(y − yi )(z − zp )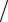 hx hy hz,
hx hy hz,
ϕn = (x − x j )(y − yi )(z − zp )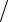 hx hy hz ,
hx hy hz ,
ϕp = (x − x j )(y − yn )(z − zi )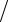 hx hy hz ,
hx hy hz ,
ϕq = −(x − xi )(y − yn )(z − zi )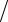 hx hy hz ,
hx hy hz ,
ϕr = (x − xi )(y − yi )(z − zi )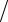 hx hy hz ,
hx hy hz ,
ϕs = −(x − x j )(y − yi )(z − zi )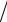 hx hy hz.
hx hy hz.
Контрольные вопросы и задания
13.1.Опишите процедуру аппроксимации заданной функции с использованием набора кусочно-постоянных пробных функций.
13.2.Опишите процедуру аппроксимации заданной функции с использованием набора кусочно-линейных пробных функций.
13.3.Опишите процедуру аппроксимации заданной функции с использованием набора кусочно-квадратичных пробных функций.
13.4.Какой смысл имеют коэффициенты разложения заданной функции по системе пробных функций?
13.5.Какая система пробных функций носит название иерархической?
13.6.В чем преимущество иерархической системы полиномов перед обычными пробными функциями?
13.7.Установите смысл коэффициентов разложения заданной функции по иерархической системе полиномов (по выбору).
13.8.Проверьте ортогональность (в указанном смысле) полиномов Лежандра для приведенной системы функций ϕi , i = 0, …, 5.
13.9.Постройте, используя указанную процедуру, дополнительные полиномы Лежандра ϕi , i = 6, …,10.
14. МЕТОД ГАЛЕРКИНА: ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
Рассматриваются последовательность и особенности применения метода Галеркина как частного случая метода моментов (взвешенных невязок) для решения ряда прикладных задач механики сплошных сред. Вопросы сходимости метода Галеркина обсуждаются в прил. 2.
14.1. Уравнение стационарной теплопроводности
Распределение температуры в тонком однородном стержне с теплоизолированной боковой поверхностью (рис. 14.1, а) описывается параболическим уравнением стационарной теплопроводности
|
|
(λT ′)′x +W = 0 |
(14.1) |
|
|
x |
|
с граничными условиями1 |
|
λTx′ |
|
x=0 = Q0 ; λTx′ |
|
x=L = − QL, |
(14.2) |
|
|
|
|
где T – температура, W – мощность внутреннего теплового источника, Q0, QL – проекции векторов тепловых потоков на внешние нормали к торцевым поверхностям стержня на левом и правом концах, λ – коэффициент теплопроводности.
L
а
qi 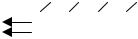


 qj
qj
h
xi xj
б
Рис. 14.1. Схема одномерной задачи теплопроводности (а); отдельный элемент рассматриваемого стержня (б)
Для упрощения выкладок величины W и λ считаются постоянными.
1 Корректность постановки этой задачи обсуждается далее.
14.1.1. Аппроксимация решения кусочно-линейными функциями
Стержень, имеющий длину L, разбивается на 4 (для определенности) равных отрезка длиной h = L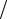 4 каждый. Для произвольного отрезка [xi , x j ]
4 каждый. Для произвольного отрезка [xi , x j ]
(рис. 14.1, б) температурное поле описывается уравнением (14.1), граничные условия (14.2) записываются в форме
λTx′ |
|
x=x = qi , |
λTx′ |
|
x=x |
= −q j , |
(14.3) |
|
|
|
|
i |
|
|
|
j |
|
где qi , q j – проекции векторов тепловых потоков на внешние нормали к грани-
цам конечного элемента. Для построения разрешающих соотношений метода Галеркина выбираются кусочно-линейные пробные функции в виде
ϕi = (x j − x)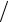 h, ϕj = (x − xi )
h, ϕj = (x − xi ) h .
h .
Эти функции позволяют искать решение задачи на отрезке [xi , x j ] в виде
Tm = Tiϕi + Tj ϕj , |
(14.4) |
где Ti, Tj – узловые значения искомого распределения температуры. Невязка уравнения (14.1), получаемая на приближении (14.4), взвешивается с использованием тех же функций ϕi и ϕj,
x j |
|
′ |
|
|
|
|
|
|
|
|
|
∫ |
(λTm′,x |
)x |
+W ϕi dx = 0; |
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
(14.5) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
j |
′ |
|
|
|
|
|
|
|
|
∫ |
(λTm′,x |
)x |
+W ϕj dx = 0. |
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
Первое из этих уравнений преобразуется к виду |
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
∫j (λTm′,x )′x ϕi dx + ∫jWϕi dx = 0, |
|
|
|
|
|
|
|
xi |
|
|
xi |
|
|
|
|
|
x j |
|
|
|
′ |
|
x j |
x j |
|
|
|
|
|
|
′ |
|
|
|
′ |
′ |
|
|
|
|
|
∫(λTm,xϕi ) xdx − |
∫ λTm,x |
ϕi,xdx + ∫Wϕidx = 0, |
|
|
|
|
xi |
|
|
|
|
|
xi |
xi |
|
|
|
|
|
|
|
|
|
|
x j |
|
x j |
|
|
|
|
|
λTm′,xϕi |
|
xxij − ∫ λTm′,xϕ′i,xdx + ∫Wϕidx = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
xi |
|
|
|
|
= 0, из послед- |
Поскольку по построению пробные функции ϕi |
|
x |
=1, |
ϕi |
|
x |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
него выражения следует
x j x j
−λTm′,x xi − ∫ λTm′,xϕ′i,xdx + ∫Wϕidx = 0.
xi xi
С учетом условия (14.3) и представления решения в виде (14.4) получается выражение
x j
ϕ′i,x dx −Tj ∫λϕ′j,x
xi
x j |
|
ϕ′i,x dx + ∫Wϕi dx = 0. |
(14.6) |
xi
Преобразования второго уравнения системы (14.5) приводят к уравнению
x j |
x j |
− q j −Ti ∫λϕ′i,xϕ′j,x dx −Tj ∫λϕ′j,x |
xi |
xi |
x j |
|
ϕ′j,x dx + ∫Wϕj dx = 0. |
(14.7) |
xi
В итоге получена система линейных алгебраических уравнений относительно узловых значений температур Ti и Tj, то есть коэффициентов разложения (14.4) решения по пробным функциям. Подсчитываются интегралы в вы-
ражениях (14.6) и (14.7):
|
|
ϕ′i,x = −1 h, |
|
x j |
x j |
|
∫λϕ′i,xϕ′i,x dx = λ∫dx h2 = λ / h, |
|
xi |
xi |
|
x j |
x j |
|
∫λϕ′i,xϕ′j,x dx = ∫λϕ′j,xϕ′i,x |
|
xi |
xi |
x |
x |
(x j − x)dx h =Wh 2 , |
∫j Wϕi dx =W ∫j |
xi |
xi |
|
ϕ′j,x =1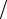 h ;
h ;
x∫j λϕ′j,xϕ′j,x dx = λx∫j dx h2 = λ/ h,
h2 = λ/ h,
x j
dx = −λ∫dx h2 =−λ/ h;
h2 =−λ/ h;
xi
x∫jWϕj dx =W x∫j (x − xi )dx h =Wh 2 .
Подстановка полученных значений в формулы (14.6) и (14.7) приводит к системе линейных алгебраических уравнений относительно искомых коэффициентов Ti и Tj ,
− qi − λTi |
h + λTj |
h + Wh 2 = 0, |
|
|
(14.8) |
|
h − λTj |
− q j +λTi |
h + Wh 2 = 0. |
|
|
|
Удобно эту систему уравнений представить в матричной форме:
−λ h λ h Ti |
qi −Wh 2 |
|
(14.9) |
|
λ h |
|
= |
. |
|
−λ h Tj |
q j −Wh 2 |
|
14.1.2. Процедура ансамблирования конечных элементов
Рассматривается композиция из четырех конечных элементов, для каждого из которых записывается собственная система уравнений вида (14.8):
|
|
|
|
|
|
|
|
|
|
|
λT h − λT h =Wh 2 |
− Q0 , |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
Q |
|
|
q2 |
|
|
|
|
|
− q |
; |
|
|
|
|
|
|
|
|
|
|
− λT h + λT h =Wh 2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
|
|
|
′ |
|
|
|
|
|
|
|
λT2 h − λT3 h =Wh 2 |
− q2′, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
|
|
q3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− λT h + λT h =Wh 2 |
− q |
|
; |
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
λT3 h − λT4 h =Wh 2 |
− q3′, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q3′ |
|
|
q4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− q |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− λT h + λT h =Wh 2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
4 |
|
|
|
|
|
|
|
′ |
|
L |
|
λT4 h − λT5 h =Wh 2 − q4′, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q4 |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− λT h + λT h =Wh 2 |
− QL . |
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
|
|
|
В итоге получена система восьми алгебраических уравнений с одиннадцатью неизвестными T1, T2 , T3 , T4 , T5 , q2 , q2′, q3 , q3′, q4 , q4′ . Для замыкания системы уравнений следует добавить три уравнения теплового баланса
q2 + q2′ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ q3′ = 0, |
|
|
|
|
(14.10) |
q3 |
|
|
|
|
|
|
+ q′ = 0. |
|
|
|
|
|
q |
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
Отметим, что внутренние переменные |
′ |
′ |
, q4 |
′ |
можно исклю- |
q2 , q2 |
, q3 , q3 |
, q4 |
чить из системы уравнений, складывая уравнения попарно и используя равенства (14.10). Так, для двух первых систем уравнений получается
+ λT h − λT h |
=Wh 2 − Q0 , |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
− λT h + λT h |
=Wh 2 |
− q |
|
, |
|
1 |
2 |
|
2 |
|
|
|
+ λT2 h |
− λT3 h =Wh 2 − q2′, |
|
|
|
|
− λT h |
+ λT h =Wh 2 |
− q |
. |
|
|
|
|
2 |
3 |
3 |
|
|
Покомпонентное сложение второго и третьего уравнений системы, с учетом (14.10), приводит к соотношениям
+ λT1 h − λT2 |
h |
= Wh 2 − Q0 , |
|
|
|
|
|
|
h + 2λT2 |
h − λT3 |
h = Wh, |
|
− λT1 |
|
|
− λT h + λT h = Wh 2 − q |
. |
|
|
2 |
3 |
3 |
|
Выполнение аналогичных преобразований для всех уравнений системы приводит к системе пяти уравнений относительно неизвестных T1, T2 , T3 , T4 , T5:
+ λT h − λT h |
|
= Wh 2 − Q0 , |
|
1 |
2 |
|
|
|
|
|
− λT h |
= Wh, |
|
− λT h + 2λT h |
|
|
1 |
2 |
3 |
|
|
|
|
− λT2 h |
+ 2λT3 h − λT4 h |
= Wh, |
|
|
|
|
|
|
|
− λT3 h + 2λT4 h − λT5 h = Wh, |
|
|
|
|
|
|
|
|
− λT h |
+ λT h = Wh |
2 − QL . |
|
|
|
|
|
|
4 |
5 |
|
В матричной форме эта система уравнений имеет вид
|
1 |
− 1 0 |
0 |
0 T1 |
|
|
|
|
2 |
− 1 |
0 |
0 |
|
|
|
|
−1 |
T |
|
λ |
|
|
|
|
|
|
|
2 |
|
|
0 |
− 1 2 |
−1 0 |
|
|
|
|
h |
T3 |
|
|
|
0 |
− 1 |
2 |
|
|
|
|
|
|
0 |
− 1 |
T |
|
|
|
|
|
|
|
|
|
|
4 |
|
0 |
0 |
0 |
−1 1 |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
5 |
|
Wh 2 − Q0 |
|
|
|
|
|
|
|
Wh |
|
|
|
|
|
|
|
Wh |
|
(14.11) |
= |
. |
|
Wh |
|
|
|
|
|
|
|
|
|
Wh 2 − QL |
|
|
|
|
|
Следует вернуться к вопросу о корректности постановки задачи (14.1)– (14.2). Неоднородная система линейных алгебраических уравнений (14.8)
λTi h − λTj h = Wh 2 − qi , |
|
|
|
|
h + λTj |
h = Wh 2 − q j |
− λTi |
|
|
|
имеет определитель, равный нулю. Также равен нулю определитель системы алгебраических уравнений (14.11). Покомпонентное сложение обоих уравнений последней системы приводит к выражению
− q j − qi +Wh = 0, |
(14.12) |
являющемуся условием баланса тепла в отдельном конечном элементе: количество тепла Wh, выделившееся за счет внутренних источников, должно быть вы-

ведено из него за счет тепловых потоков qi и qj с торцов. Это становится очевидным, если вспомнить, что решается стационарное уравнение теплопроводности, решением которого является температурное поле, установившееся за бесконечно большой промежуток времени. Невыполнение балансового соотношения (14.12) приведет либо к накоплению тепла в стержне (при Wh > qi + q j ) и, следовательно, к бесконечно высоким температурам, либо –
к принудительному отводу тепла из стержня (при Wh < qi + q j ) и, соответствен-
но, к бесконечно низким температурам. При точном выполнении соотношения (14.12) стержень будет находиться в состоянии термического равновесия при любом распределении температуры, удовлетворяющем уравнению (14.11). Это означает, что решение оказывается неединственным, то есть исходная задача сформулирована некорректно. Это следует из уравнений (14.1)–(14.2), которые определяют решение задачи с точностью до постоянной величины.
Вырожденность системы уравнений (14.8) на уровне отдельного конечного элемента приводит к вырожденности системы алгебраических уравнений (14.11) для всего ансамбля конечных элементов. В этом случае суммирование всех уравнений системы (14.11) также приводит к балансовому соотношению Q0 + QL =WL. Несмотря на некорректность постановки задачи (14.1)–(14.2),
рассмотренный порядок формирования разрешающих соотношений является верным и используется для построения решения прикладных задач. Для корректной постановки задачи следует изменить граничные условия. Пусть на ле-
= ~
вом конце стержня поддерживается постоянная температура T x=0 T . Для уче-
та этого граничного условия к полученной системе (14.11) следует добавить
= ~
уравнение T1 T (коэффициент T1, как это уже отмечалось ранее, аппроксими-
рует значение искомой температуры в первом узле) и считать поток тепла Q0 на левом конце стержня неизвестным. В этом случае получается система шести
уравнений с неизвестными тель,
T |
|
|
|
1 |
|
|
+ λT |
h − λT |
h |
|
1 |
2 |
|
− λT |
h + 2λT |
h |
|
1 |
2 |
|
|
|
− λT2 |
|
|
|
h |
|
|
|
|
|
|
|
|
T1, T2 , T3 , T4 , T5 , Q0 , имеющая ненулевой определи-
|
~ |
|
|
=T , |
|
|
=Wh 2 − Q0 , |
− λT3 h |
=Wh, |
|
+ 2λT3 h − λT4 h |
=Wh, |
|
− λT3 h + 2λT4 h − λT5 h =Wh, |
|
− λT h |
+ λT h =Wh |
2 − QL . |
4 |
5 |
|

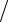 hx hy hz,
hx hy hz,
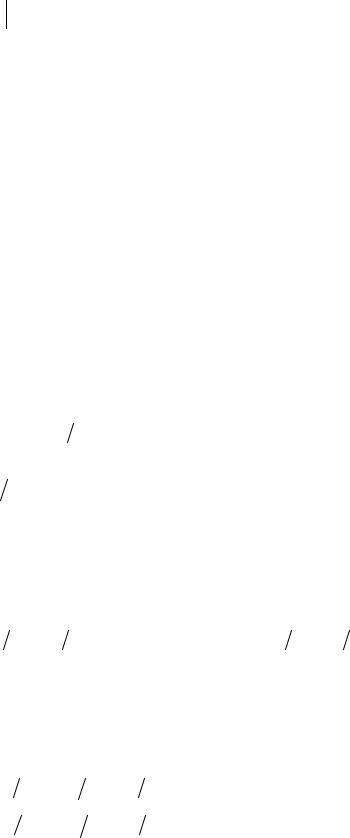






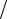


 q
q 4 каждый. Для произвольного отрезка
4 каждый. Для произвольного отрезка 

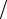
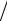
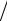 h
h