v′y,t + vxv′y,x + vy v′y, y = −Py′ + Re−1 (v′y′,xx + v′y′, yy ), |
(16.5) |
v′x,x + v′y,y = 0. |
(16.6) |
Здесь обозначено: x, y – координаты произвольной точки рассматриваемой двумерной области, t – время, P – давление, Re = LV 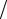 ν – число Рейнольдса, L,
ν – число Рейнольдса, L,
V – характерные размер области и скорость течения, ν – коэффициент вязкости жидкости. Уравнение несжимаемости (16.6) при подстановке формул (16.2), то есть при использовании функции тока, –
v′x,x + v′y, y = ψ′xy′ − ψ′yx′ = 0
– выполняется тождественно. Дифференцирование уравнения (16.4) по переменной y, уравнения (16.5) – по переменной x приводит к выражениям
(v′x, y )′t + v′x, y v′x,x + vxv′x′, yx + v′y, y v′x, y + vy v′x′, yy = −Pyx′′ + Re−1 (v′x′′, yxx + v′x′′, yyy ),
(v′y,x )′t + v′x,xv′y,x + vxv′y′,xx + v′y,xv′y, y + vy v′y′,xy = −Pxy′′ + Re−1 (v′y′′,xxx + v′y′′,xyy ).
Вычитание первого выражения из второго дает соотношение
(v′y,x −v′x,y )t′ +vx (v′y,x −v′x,y )′x +vy (v′y,x −v′x,y )′y +v′y,y (v′y,x −v′x,y )+v′x,x (v′y,x −v′x,y )=
= Re−1 (v′y,x − v′x, y )″xx |
+ (v′y,x − v′x, y )″yy . |
|
|
С использованием уравнения несжимаемости (16.6) и определения (16.3) функции завихренности ω полученное соотношение принимает вид дифференциального уравнения
′ |
′ |
′ |
−1 |
′′ ′′ |
(16.7) |
ωt |
+ vxωx + vy ωy = Re |
|
(ωxx + ωyy ). |
Подстановка формул (16.2) в выражение (16.3) позволяет получить дифференциальное уравнение относительно функции тока ψ,
ω= v′y,x − v′x, y = (− ψ′x )′x − (ψ′y )′y ,
′′ |
′′ |
(16.8) |
ψxx + ψyy = −ω. |
Выполненные преобразования позволили тождественно удовлетворить уравнению несжимаемости (16.6) и исключить из уравнений Навье–Стокса давление P. Решение системы уравнений (16.7) и (16.8) позволяет найти распределения функций ω и ψ, а использование соотношений (16.2) – определить



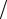
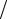
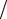
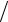
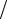 ψ
ψ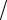
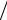
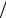 ψ
ψ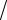
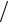
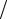 ψ
ψ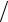
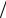 ψ
ψ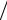
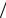 ψ
ψ