2.4. Расчет концентрации электронов и положения уровня Ферми в дырочном полупроводнике

При расчете концентрации электронов и положения уровня Ферми в дырочном полупроводнике воспользуемся методикой, которая применялась нами для анализа статистики носителей заряда в электронных полупроводниках. Полагаем, что при комнатной температуре проводимость дырочного полупроводника определяется, главным образом, дырками, образовавшимися при ионизации акцепторной примеси. Дырки в полупроводниках p-типа проводимости называютосновными носителями заряда, а электроны -неосновными носителями заряда.

Каждый однократно ионизированный атом акцепторной примеси (акцептор) можно рассматривать как примесный центр, захвативший электрон. Поэтому первое уравнение электронейтральности (1.38) для дырочного полупроводника имеет следующий вид:

p_p=, (2.28)

где p_p - концентрация свободных дырок в валентной зоне полупроводника, м^-3;- концентрация ионизированных акцепторов на примесных уровнях, м^-3.

Умножая левую и правую части уравнения (2.28) на значение p_p и решая полученное уравнение относительноp_p, получим выражение для закона действующих масс в дырочном полупроводнике в виде, откуда следует, что концентрация дырок в полупроводникеp-типа проводимости определяется уравнением вида

. (2.29)

Для определения концентрации дырок p_pи заряженных акцепторовв дырочном полупроводнике, применяется тот же метод, что и для расчета концентраций носителей заряда в электронном полупроводнике. В результате получим, что концентрация дырок в дырочном полупроводнике рассчитывается по формуле

. (2.30)

Концентрация отрицательных ионов на примесных уровнях в дырочном полупроводнике определяется из выражения

, (2.31)

где N_a- эффективная плотность состояний электронов на уровнях акцепторной примеси, фактически представляющая концентрацию атомов акцепторной примеси, м^-3.

Подставив значения p_p ииз выражений (2.30) и ( 2.31) в уравнение (2.29), получим, что концентрация дырок в дырочном полупроводнике рассчитывается по формуле

, (2.32)

где W_a= W_a-W_v- энергия ионизации акцепторного уровня.

Так же, как и в случае электронных полупроводников, формула (2.32) справедлива при расчетах концентрации основных носителей заряда в дырочных полупроводниках для ограниченного диапазона температур - от 0 до 30...70 К. Для дырочных полупроводников остаются справедливыми также понятия температуры истощения и появления собственной проводимости при сильном нагреве полупроводника. Значение температуры истощения Т=Т_s и температуры появления собственной проводимостиТ=Т_iрассчитываются по формулам типа (2.22) и (2.23) с подстановкой в них соответствующих значений определяемых величин:

, (2.33)

. (2.34)

Температурная зависимость концентрации носителей заряда pв полупроводникеp-типа, построенная в координатахln p=f(1/T), аналогична представленной выше на рис. 2.3 для электронного полупроводника. Эта зависимость характеризуется областями слабой ионизации, истощения и перехода к собственной проводимости.

Для определения положения уровня Ферми в дырочном полупроводнике воспользуемся очевидным равенством p_p=, справедливым в диапазоне комнатных температурТ300 К. Подставляя в это равенство значенияp_pииз выражений (2.30) и (2.31) и беря натуральные логарифмы от левой и правой частей, получим следующее выражение

. (2.35)

И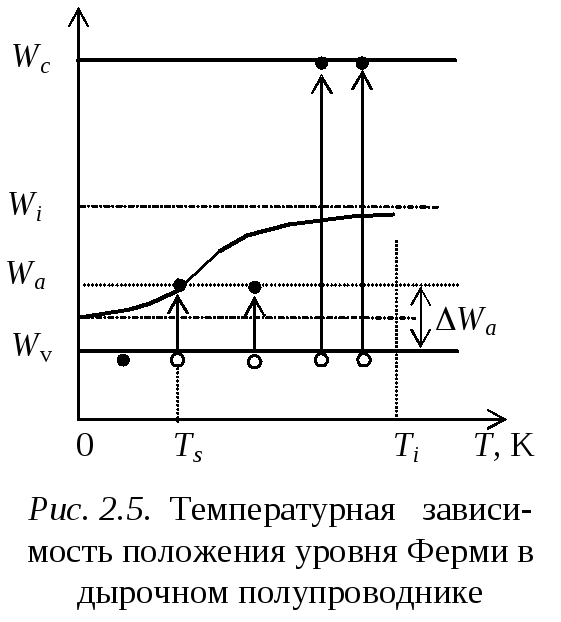з этого выражения получаем, что значение энергии, соответствующей положению уровня ФермиW_Fв дырочном полупроводнике рассчитывается по формуле

. (2.36)

График функции W_F=f(T) приведен на рис. 2.5. Анализ этого рисунка и формулы (2.36) позволяет сделать следующие выводы.

При Т=0 уровень Ферми в дырочном полупроводнике располагается посередине между потолком валентной зоны и уровнем акцепторной примеси, то естьW_F =(W_v+W_a)/2.

С возрастанием температуры энергия уровня Ферми W_Fначинает постепенно увеличиваться и при температуре истощенияТ=Т_s пересекает уровень акцепторной примесиW_a. ПосколькуW_F=W_a, то равенство (2.35) можно записать в виде lnN_a=lnN_v+(W_v-W_F)/kT, откуда следует, что

. (2.36)

Подставляя в выражение (2.36) значение Т=Т_sиз формулы (2.33) и, учитывая, чтоW_a=W_a-W_v, действительно получаем, чтоW_F=W_a.

При температурах, больших температуры истощения, положение уровня Ферми смещается вверх к середине запрещенной зоны, что свидетельствует о плавном переходе от дырочной к собственной проводимости полу проводника.

В полупроводнике p-типа в диапазоне температурT_sTT_iконцентрация основных носителей (дырок)p_p=N_a, а концентрация неосновных носителей – ,электронов, рассчитывется исходя из закона равновесия масс

. (2.37)

Заметим, что примесные энергетические уровни, для которых характерна небольшая энергия ионизации, составляющая несколько сотых долей эВ, принято называть мелкими уровнями. Наряду с примесями, создающими мелкие уровни, для легирования полупроводников используют примеси, при введении которых в запрещенной зоне создаются уровни с энергией ионизации порядка 0,1...0,4 эВ, сообщающие полупроводнику качественно новые свойства. Такие уровни называютглубокими уровнями (центрами). В качестве примесей, создающих глубокие примесные уровни в запрещенной зоне полупроводников используют элементы 1-й группы (Cu, Ag, Au), 6-й группы (S), элементы группы железа (Fe, Co, Ni) и некоторые другие.