22. Определение нагрузок и воздействий. Постоянные нагрузки и воздействия в случае невыгодных сочетаний этих конструкций. Понятие о грузовой площадке.

СНиП приводит 6 постоянных нагрузок и воздействий: № 1 - № 6.

Нагрузка № 1 называется собственный вес конструкции.Эта нагрузка всегда действует; не учитывается только, когда она пренебрежительно мала по отношению к другим нагрузкам.

Она вертикальна – направлена сверху вниз, постоянная. Определяется путем взвешивания по табличным данным, по графикам, номограммам, формулам и путем расчета по проектным объемам.

Последний метод – самый распространенный при проектировании инженерных сооружений, причем могут использоваться и указанные выше способы. Нагрузка – от собственного веса конструкции. N = ۷ ^. ﻻ

Для сложных конструкций необходима разбивка их на элементарные объемы. Например, подсчитаем нагрузку от собственного веса (расчетную) одного квадратного метра ездового полотна городского путепровода.

Задаемся типом покрытия – асфальтобетон.

Защитный слой – из цементобетона (4 см).

Гидроизоляция – 1 см.

Выравнивающий слой – 3 см.

Определяем объем каждого слоя:

V_покр. = 1 ^. 1 ^. 0,07 = 0,07 м³

ﻻ _покр. = 2,3 т/м³

ﻻ ж/б = 2,5 т/м³

ﻻ _{гидроиз.} = 1,5 т/м³

ﻻ _защ. = 2,2

Нормативное значение нагрузки – N

N = V_пок. ﻻ _пок + V_защ. ﻻ _защ + V_гид. ﻻ _{гидроиз} + V_вырав. ﻻ _вырав.

Расчетное значение определяется путем умножения нормативной нагрузки на свое соответствующее значение коэффициента надежности ﻻ_f

ﻻ_f покрытия сооружений в городских условиях = 2,0, для остальных слоев ﻻ_f = 1,3.

23. Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модельидеализированногодеформируемоготела, включающая следующие допущения и упрощения:

• Гипотезасплошности и однородности:материалпредставляет собойоднороднуюсплошную среду;свойстваматериала во всех точках тела одинаковы и не зависят от размеров тела.

• Гипотеза об изотропностиматериала:физико-механическиесвойства материала одинаковы по всем направлениям.

• Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.

• Гипотеза (допущение) о малости деформаций: деформациив точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.

• Допущение о справедливости закона Гука: перемещенияточекконструкциивупругой стадииработы материала прямо пропорциональны силам, вызывающим эти перемещения.

• Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешнихфакторовравенсуммерезультатов воздействия каждого из них, прикладываемого в отдельности, и не зависит отпоследовательностиих приложения.

• Гипотеза Бернуллио плоских сечениях: поперечныесечения, плоские и нормальные к осистержнядо приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

• Принцип Сен-Венанна: в делениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.

Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.

Теории прочности

Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупкоипластично. В зависимости от условий (температуры, распределения напряжений, вида нагрузки и т. п.) большинство материалов может быть отнесено к хрупким, пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред не всегда достаточен.

Математически теория разрушения выражается в виде различных критериев разрушения, справедливых для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение, это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.

Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:

1. Теория наибольших нормальных напряжений.

2. Теория наибольших деформаций.

3. Теория наибольших касательных напряжений Треска.

4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса.

5. Теория Мора.

Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона.Кулон(Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал вниманиеА. А. Гвоздев, который доказал неприменимость теории Мора для бетона.[1]

На смену «классическим» теориям прочности в современной практике пришли многочисленные новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:

Друкера-Прагера(Drucker-Prager).

Бреслера-Пистера(Bresler-Pister) — для бетона.

Вильяма-Варнке(Willam-Warnke) — для бетона.

Хенкинсона(Hankinson)- эмпирический критерий, используемый для ортотропных материалов типа древесины.

Хила(Hill) — для анизотропных тел.

критерий Tsai-Wu — для анизотропных материалов.

критерий Hoek-Brown -для скальных массивов.

Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.

Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементови вычислительной техники. При макро-моделировании предварительно выполняетсягомогенизация— условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий.Критерии разрушения каменных конструкцийучитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.

Применение

Методы сопротивления материалов широко используются при расчете несущих конструкцийзданий и сооружений, в дисциплинах связанных спроектированиемдеталей машини механизмов.

Как правило, именно из-за оценочного характера результатов, получаемых с помощьюматематических моделейэтой дисциплины, при проектировании реальных конструкций все прочностные характеристикиматериалови изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).

26.

Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет её средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. По мнению автора рассматриваемого коэффициента К. Пирсона — коэффициент вариации эффективнее абсолютного показателя вариации^[3].

Известно, что коэффициент вариации может быть записан посредством долей^[4]:

где .

где  — математическое ожидание. Эта формула применяется для вероятностных моделей.

КОЭФФИЦИЕНТ ИЗМЕНЧИВОСТИ ВЫБОРКИ — ,

где m₂ — второй выборочный момент, x — выборочное среднее. Характеризует изменчивость изучаемого признака. Широко используется при оценке ошибок подсчетов.

Коэффициент надежности

установленный нормами расчета коэффициент, учитывающий возможность отклонения нагрузки (коэффициент надежности по нагрузке) или прочности материала (коэффициент надежности по материалу) от нормативных их значений, приводится в СНиП. Для примера –коэффициенты надежности по нагрузкам.

27.

Расчётная схема сооружения — в строительной механике, упрощённое изображение сооружения, принимаемое для расчёта. Различают несколько видов расчётных схем, отличающихся основными гипотезами, положенными в основу расчёта, а также используемым при расчёте математическим аппаратом. Чем точнее расчётная схема соответствует действительному сооружению, тем более трудоёмок его расчёт.

Расчётная схема состоит из условных элементов: стержней, пластин, оболочек, массивов и связей.

Стержни используют в расчётных схемах стержневых конструкций (стоек, балок, арок и др.), систем из таких конструкций (ферм, рам, сетчатых оболочек), а также для приближённого расчёта плоскостных конструкций (например, несущих стен зданий).

Пластины треугольной и прямоугольной формы являются основными конечными элементами при расчёте методом конечных элементов плоскостных конструкций (стен и плит перекрытий зданий).

Оболочки являются расчётной схемой различных пространственных конструкций (куполов, сводов, оболочек).

Массивы в расчётных схемах используются, как правило, в качестве недеформируемых опор пролётных конструкций, опирающихся на сжимаемое основание.

Связи в расчётных схемах соединяют между собой отдельные элементы, а также конструкцию с основанием. В расчётных схемах связи различаются по числу степеней свободы, которые они отнимают от системы. Связи могут быть дискретные и распределённые (континуальные). Стержни и пластины, соединённые распределёнными связями называются составными стержнями и пластинами. ^[1]

Расчётные схемы многоэтажных зданий

Многоэтажное здание является сложной пространственной системой, которая в зависимости от этажности, особенностей конструктивной системы и действующих нагрузок, рассчитывается с разной степенью детализации с использованием различных расчётных схем. В современной практике проектирования расчёт здания, как правило, выполняется по специальным программам с применением вычислительной техники. ^{[2] [3]}

При одномерной расчётной схеме здание рассматривается как консольный тонкостенный стержень или система стержней, упруго или жёстко закреплённых в основании. Предполагается, что поперечный контур стержня или системы стержней неизменяем.

При двухмерной расчётной схеме здание рассматривается как плоская конструкция, способная воспринимать только такую внешнюю нагрузку, которая действует в её плоскости. Для определения усилий в вертикальных несущих конструкциях условно принимается, что все они расположены в одной плоскости и имеют одинаковые горизонтальные перемещения в уровне перекрытий.

При трёхмерной расчётной схеме здание рассматривается как пространственная система, способная воспринимать приложенную к ней пространственную систему нагрузок.

Двухмерные расчётные схемы стены с регулярно расположенными по вертикали проёмами (a): составной стержнь (b); многоэтажная рама (c); пластинчатая система МКЭ (d)

В дискретных расчётных схемах неизвестные усилия или перемещения определяют для конечного количества узлов системы путём решения систем алгебраических уравнений. Дискретные расчётные схемы наиболее приспособлены для расчёта методом конечных элементов. Такие схемы широко используют для моделирования не только стержневых систем, но и сплошных пластин и оболочек.

В дискретно-континуальных расчётных схемах неизвестные силовые факторы или перемещения задают в виде непрерывных функций вдоль одной из координатных осей. Неизвестные функции определяются решением краевой задачи для системы обыкновенных дифференциальных уравнений.

В теории составных стержней принимается, что стержни деформируются только от продольных сил и изгиба. Между тем вертикальные диафрагмы жесткости многоэтажных зданий часто имеют такие соотношения размеров в плане и по высоте здания, для которых необходимо учитывать деформации сдвига.

28.

Чтобы обеспечить безопасные условия эксплуатации зданий и сооружений, производят расчет конструкций. Строительные конструкции рассчитывают в два этапа: 1) статический (или динамический) расчет, который заключается в составлении расчетных схем, наиболее близко отвечающих работе конструкции в реальных условиях и определении внутренних усилий (изгибающих моментов М, поперечных Qи продольныхNсил и др.) в опасных сечениях проектируемых конструкций. Этот расчет производится по формулам сопротивления материалов и общим правилам строительной механики; 2) конструктивный расчет - выбор материала, рациональных форм и размеров сечения, марок и класса материала (камня, бетона), класса стали, породы и качества древесины и т.д. Известны три метода конструктивного расчета: 1) по допускаемым напряжениям; 2) по разрушающим нагрузкам; З) по предельным состояниям Проектировщики применяют третий метод расчета. Цель такого расчета - не допускать предельных состояний при эксплуатации в течение всего срока службы конструкции, здания или сооружения. Расчет выполняют исходя из того, чтобы значения усилий, напряжений, деформаций, перемещений не превышали предельных значений, устанавливаемых СНиП. Значения нагрузок, действующих на конструкции, прочностные характеристики материалов, из которых они сделаны, и условия их эксплуатации обладают определенной изменчивостью и могут отличаться от установленных нормами. В расчете по методу предельных состояний это учитывается введением ряда коэффициентов перегрузкиn, условий работыmв, надежности и др. Числовые значения этих коэффициентов приводятся в СНиП.

Любая задача расчета конструкций имеет три стороны: статическую (или динамическую), геометрическую и физическую.

Статическая(динамическая) сторона задачи заключается в установлении связи между внешними нагрузками, действующими на конструкцию, и внутренними усилиями в любом ее сечении, которая определяется условиями статического (динамического) равновесия. Поскольку внутренние усилия заранее неизвестны, приходится привлекать геометрические и физические соотношения.

Геометрическиесоотношения связывают перемещения и деформации конструкции.

Физическиеопределяют закон, по которому напряжения зависят от деформаций.

31.Основными причинами, приводящими к авариям строительных конструкций, являются: ошибки при проектировании; недостаточный технический надзор и контроль качества при изготовлении и монтаже; нарушение правил эксплуатации зданий и сооружений; несовершенство норм и технических условий; ошибки в выдаче исходных данных для проектирования. Указанные ошибки могут привести к внезапному отказу (аварии) или постепенному отказу (аварийному состоянию) сооружения.

29.Воздействие агрессивной окружающей среды на строительные конструкции при эксплуатации может привести к коррозии бетона, арматуры, закладных деталей, а также к преждевременному износу каменных и бетонных конструкций, может вызвать разрушение и гниение деревянных элементов и как следствие — снижение несущей способности конструкций здания в целом. Поэтому при эксплуатации зданий необходимо определить участки коррозионного повреждения бетона, арматуры, характер и степень этих повреждений, а также установить степень износа каменных конструкций и т.д.

В процессе эксплуатации необходимо обеспечивать достаточную вентиляцию помещений для удаления агрессивных газов, защищать элементы зданий от увлажнения атмосферными осадками и грунтовыми водами, повышать коррозионную стойкость бетонных и железобетонных конструкций путем поверхностной и объемной обработки поверхностно-активными веществами, устраивать антикоррозионные покрытия.

32.Надежность- сложное свойство, которое, в зависимости от назначения объекта и условий его применения, характеризуется безотказностью, долговечностью, ремонтопригодностью и сохраняемостью. Главным показателем надежности несущей конструкции является безопасная ее работа под действием внешних нагрузок и различных воздействий возникающих при эксплуатации( температурных, коррозионных, сейсмических и др.)

Безопасность – свойство, показывающее возможность объекта непрерывно сохранять работоспособное состояние в течении заданного времени.

Долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояние при установленной системе технического обслуживания и ремонта.

Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений, а также поддержанию и восстановлению работоспособности проведением технического обслуживания и ремонтов. Количество ремонтопригодности определяется затратами времени, труда и средств.

Ремонтопригодность определяет доступность, контролепригодность, агрегатирование, легкосъемность, унификацию и тд.

Сохраняемость – свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение хранения и после него и ( или ) транспортирования. Наиболее эффективные методы повышения сохраняемости – консервация, применение специальных защитных покрытий и пропитывающих составов, профилактическое обслуживание хранящихся объектов, повышение транспортабельности объектов, защита от старения полимеров.

30.Плотность распределения прочности материала

33. Закономерности случайных явлений для строительных конструкций.

Событие - качественный или количественный результат опыта, осуществляемого при определенных условиях. Например, событие - попадание предела текучести стали в интервал от 240 до 260 МПа. Событие может быть случайным, достоверным или невозможным. Объективная математическая оценка возможности реализации случайного события - вероятность. Вероятность есть объективная мера возможности наступления события независимо от того, является ли оно массовым или нет. В жизни все (полуинтуитивно) применяют вероятностные оценки будущим событиям и весьма успешно.

Вероятностное поведение конструкций

Роль случайных закономерностей в поведении конструкции

Поведение конструкции на различных стадиях их функционирования носит случайный характер. Рассмотрим причины и природу этого явления.

Одним из направлений современного развития теории расчета строительных конструкций является решение проблемы оценки надежности и взаимосвязанной с ней долговечностью зданий и сооружений. Кардинальный вопрос о способности конструкции сопротивляться внешним воздействиям в течение срока её службы с обеспечением требуемых эксплуатационных качеств может быть решен обоснованно и достоверно только на основе применения вероятностных подходов, лежащих в основе фундаментальных законов природы

Строительным конструкциям, как показали исследования в нашей стране и за рубежом, свойственна случайная природа поведения на различных стадиях их функционирования. Опыт эксплуатации мостов, зданий и сооружении свидетельствует, что надежность и безотказная работа конструкций зависит от большого количества изменчивых факторов, определяющих как внешнее воздействие нагрузок при монтаже и эксплуатации, так и несущую способность конструкции по различным признакам выхода её из строя.

34. Математическое ожидание случайной величины прочности материала.

Математическое ожидание случайной величины

Математическое ожидание случайной величиныС законом распределения (35.1) определяется формулой (35.9) Если случайная величинаЗадана законом распределения (35.2), то (35.10) При условии, что ряд сходится. Математическое ожидание называется средним значением, а также центром распределения. Для математического ожидания употребляются и другие обозначения: Математическое ожидание непрерывной случайной величины, все значения которой принадлежат отрезку, определяется формулой (35.11) Если случайная величина может принимать любые значения из промежутка , то (35.12) При условии, что интеграл сходится. Математическое ОНЬЩшие случайной величины обладает следующими свойствами. 1.  Математическое ожидание случайной величины заключено между ее наименьшим и наибольшим значениями. 2.  Математическое ожидание постоянной равно этой постоянной: 3.  Постоянный множитель можно выносить за знак математического ожидания, т. е. 4.  Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: 5.  Математическое ожидание произведения двух независимых величин равно произведению их математических ожиданий: Пример 3S.3. Найти математическое ожидание дискретной случайной величины по ее закону распределения, заданному схемой По формуле (35.9) находим: Пример 35.4. Найти математическое ожидание непрерывной случайной величины, указанной в примере 35.1. По формуле (35.12) получаем

Математическое ожидание - достоверная величина, т.к. вероятность того, что приn=испытаниях мы получим среднее арифметическоеМ(X)=равна 1.

М(с)=с,М(сx) = сМ(x),гдес– неслучайное число.

Для независимых с.в. Х₁иХ₂

М(x₁+x₂)=М(x₁)+М(x₂), М(x₁x₂)=М(x₁)М(x₂), М(x²)=[М(x)]²+D(x).

К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n. Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в.

35. Биноминальное распределение случайных величин.

Биноминальный закон распределения случайной величины

 Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.

 Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:

 

где p^n - вероятность того, что при n испытаниях событие А наступит n раз;

qⁿ - вероятность того, что при n испытаниях событие А не наступит ни разу;

- вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n-m раз;

- число сочетаний (комбинаций) появления события А и Ā.

 Числовые характеристики биноминального распределения:

 М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

 D(m)=npq - дисперсия частоты появления события. А;

 - среднее квадратическое отклонение частоты.

36. Распределение случайных величин Пуассона.

Распределе́ние Пуассо́на моделирует случайную величину, равную числусобытий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью инезависимодруг от друга.

Определение 

Выберем фиксированное число и определимдискретное распределение, задаваемое следующейфункцией вероятности:

,

где

обозначаетфакториал,

—основание натурального логарифма.

Тот факт, что случайная величина имеет распределение Пуассона с параметром, записывается:.

37. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид

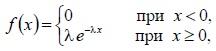
где λ – постоянная положительная величина

Функция распределения

Вероятность попадания в интервал

Математическое ожидание

Дисперсия

Среднее квадратическое отклонение

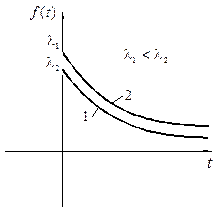
38. Нормальное распределение,также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:

где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.

Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Плотность вероятности

Функция распределения

39. Безотказность – свойство изделия непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки. Под работоспособным состоянием (кратко – работоспособно- стью) понимают состояние изделия, при котором оно способно выполнять предписанные ему функции, имея значения выходных параметров в пределах норм, оговоренных в технической документации.

40. Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта и транспортирования. Или надежность также – устойчивость качества по отношению ко всем возможным возмущениям. Надежность – количественный показатель (промежуток времени, число рабочих циклов, число километров и т.д.).

В зависимости от назначения системы и условий ее эксплуатации надежность включает свойства: 1) безотказность; 2) долговечность; 3) ремонтопригодность; 4) сохраняемость и любые их сочетания.

Безотказность – вероятность безотказной работы конструкции за определенный промежуток времени.

Долговечность – вероятный промежуток времени безотказной работы конструкции.

Ремонтопригодность – вероятность того, что неисправная система может быть восстановлена за заданное время.

Содержание теории надежности – разработка методов оценки надежности систем и создание систем, обладающих заданными показателями надежности и долговечности.

Задачи расчета на надежность состоят в определении вероятности выхода конструкции из строя в заданных условиях, нахождении по заданной экономически целесообразной надежности требуемых размеров конструкции, допустимых нагрузок или оптимального срока эксплуатации, а также оценки надежности системы по имеющимся оценкам надежности составляющих ее элементов. В задачу теории надежности строительных конструкций входит также обоснование процедур нормирования расчетных характеристик. Специфика теории надежности строительных конструкций состоит в необходимости учета случайных свойств нагрузок и воздействий на сооружения, а также учета совместного действия случайных нагрузок на систему со случайными прочностными характеристиками.

Основное понятие теории надежности – отказ – событие, состоящее в нарушении работоспособности системы. Понятие отказа близко по смыслу к понятию предельного состояния. К предельным состояниям 1-й группы относятся: общая потеря устойчивости формы, потеря устойчивости положения, любое разрушение, переход в изменяемую систему, качественное изменение конфигурации; состояния, при которых возникает необходимость прекращения эксплуатации в результате текучести материала, сдвига в соединениях, ползучести или чрезмерного раскрытия трещин. Предельные состояния 2-й группы – недопустимые деформации конструкций в результате прогиба, поворота или осадок, характеризуемых разностью вертикальных перемещений узлов, отнесенных к расстоянию между ними, креном сооружения в целом, относительным прогибом или выгибом, кривизной элемента, относительным углом закручивания, горизонтальным или вертикальным смещением элемента или сооружения в целом, углом перекоса или поворота. К предельным состояниям 2-й группы относятся также недопустимые колебания конструкции, изменение положения, образование или раскрытие трещин.

Примеры отказов - обрушения, опрокидывания, потеря устойчивости, хрупкое разрушение, большие деформации и прогибы, механический или коррозионный износ, растрескивание и т.д.

Отказы вызваны влиянием случайных факторов, поэтому они носят случайный характер. За показатель (меру) надежности системы может быть принята вероятность Р безотказной работы в течение всего срока службы Т.

Недостатки теории надежности - сложно получить опытные данные в количестве достаточном для последующей их обработки методами теории вероятностей. Сложно длительный срок проводить испытания конструкции для получения надежных выводов о ее долговременной работе

44. Корреляционный анализ

Корреляционный анализ – это совокупность методов обнаружения связи между двумя показателями в одной выборке (например, между размерами балки и её несущей способностью) либо между двумя различными выборками (например, при сравнении конструкций).

Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.

Коэффициент корреляции — это величина, которая может варьировать в пределах от +1 до -1.

Если с увеличением одного показателя увеличивается и второй, то коэффициент корреляции положителен (положительная корреляция), если же второй наоборот уменьшается, то коэффициент отрицателен (отрицательная корреляция), или если показатели полностью независимы друг от друга, коэффициент равен нулю (нулевая корреляция).

Коэффициенты стьюдента.

Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины :

x₁, x₂, x₃, ... x_n.

Величину, которая будет оценивать результаты измерений, обозначим 

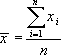
где – n число измерений.

Если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое).

Средней квадратичной ошибкой отдельного результата измерения называется величина

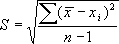
Среднеквадратичной ошибкой среднего арифметического называется величина

С уменьшением числа измерений уменьшается точность измерения.

Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом  Стьюдента t.

Опуская теоретические обоснования его введения, заметим, что

Δx = · t.

где Δx – абсолютная ошибка для данной доверительной вероятности; – среднеквадратичная ошибка среднего арифметического.

Ошибка   характеризует точность, с которой получено среднее значение измеренной величины . Результат записывается в виде:

45. Недостатки принятого полувероятностного расчёта конструкции.

Недостаток полувероятностного метода заключается в том, что он не даёт 100% надёжность конструкции. Для увеличения надёжности, в этом методе, используют коэффициенты надёжности.

Однако, всегда используется полувероятностные методы расчёта, так как, вероятностные методы расчёта очень сложные и всё равно не дают 100% надёжность конструкции. Поэтому, всё равно приходиться вводить коэффициент надёжности, так как эта конструкция имеет небольшие погрешности при её изготовлении в размерах, несущей способности и т.д.

К полувероятностным способам оценки надежности относятся методы расчета по предельным состояниям.

Различают две группы предельных состояний:

1. При наступлении предельных состояний первой группы конструкция становится полностью непригодной к эксплуатации.

2. Наступление предельных состояний второй группы вызывает затруднение нормальной эксплуатации, связанной с необходимостью снижения величины нагрузки или скорости движения из-за возникновения чрезмерных деформаций перемещений колебаний а также снижения долговечности вследствие образования и недопустимого раскрытия трещин.

Расчеты по предельным состояниям должны гарантировать невозможность наступления любого предельного состояния на всех стадиях работы изготовления хранения транспортировки и монтажа.