
shpory_matan
.docx|
14.
Объем.
Как отмечалось выше, объем цилиндроида,
т.е. тела, ограниченного поверхностью
Пример.
Вычислить объем тела, ограниченного
поверхностями
Замечание
1.
Если тело, объем которого ищется,
ограничено сверху поверхностью
Площадь плоской фигуры.
Если
составить интегральную сумму для
функции
Пример
2.
Вычислить площадь, ограниченную
линиями
|
2.
Пусть
имеем два ряда с положительными
членами:
Теорема
1.
Если члены ряда (2) не больше соответствующих
членов ряда (3), т.е.
Пусть
Пример.
Ряд
Теорема
2.
Если члены ряда (2) не меньше соответствующих
членов ряда (3), т.е.
Пример.
Ряд
Теорема
3.
Если существует конечный и отличный
от нуля предел,
|
6. Знакочередующиеся ряды.
Члены
знакочередующегося ряда имеют
чередующиеся знаки:
Теорема
Лейбница. Если в знакочередующемся
ряде
Пример.
Ряд
|
3.
Теорема.
Если в ряде с положительными членами
Доказательство.
Пусть
Пусть
Замечание 1.
Если
Если |
4.
Если
для ряда с положительными членами
Пусть
Пусть
Пример.
Замечание:
Если
Пример.
Для гармонического ряда
Пример, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
19. Понятие события. Под случайным событием будем понимать все то, что может произойти, а может и не произойти при проведении испытаний. Например, стрелок стреляет по мишени. Выстрел это испытание, попадание в определенную область мишени – это случайное событие. События обозначается заглавными латинскими буквами. Событие U называется достоверным, если оно обязательно происходит при каждом испытании. Событие V называется невозможным, если оно не происходит не при каком испытании 20. Классическое определение вероятностей. Пусть
в урне имеются 3 белых, 2 черных одинаковых
шара. Если наудачу извлекается шар,
то возможно 5 элементарных исходов
(можно вынуть любой из трех белых и
любой из двух черных шаров). Такие
исходы образуют полную группу, и они
равновозможные (равновероятные), так
как нет основания считать, что появление
какого-либо шара будет предпочтительней.
Мы рассмотрели все возможные исходы.
Мы рассматриваем возможность вынуть
белый шар, тогда интересующими нас
исходами будет появление из 3 белых
шаров. Эти исходы назовем благоприятствующими
нашим событиям. Отношение благоприятствующих
исходов к общему числу всех исходов
называется вероятностью событий A
и обозначается
|
7.
Знакопеременный
ряд
Знакопеременные ряды – если среди членов есть положительные и отрицательные.
Числа
Теорема.
Если знакопеременный ряд
Доказательство.
Пусть
Пусть
1. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов. 2. Если ряд сходится условно, то, какое бы ни выбрали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась равной А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки окажется расходящимся. сумма ряда после перестановки уменьшилась вдвое. Это говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых. |
8.
Ряд
Пример.
10.
1.
Если степенной ряд
Замечание. Полученный ряд снова можно почленно дифференцировать и продолжать сколько угодно раз. 2.
Пусть дан ряд (1). Тогда
|
9.
Степенным рядом называется функциональный
ряд вида
Теорема Абеля.
Если
степенной ряд сходится при некотором
значении
Если
ряд расходится при некотором значении
Из
теоремы
Абеля
следует, что если
Теорема. Областью сходимости степенного ряда является интервал с центром в начале координат. Определение. Интервалом сходимости степенного ряда называется такой интервал от R до R, что для всякой точки x, лежащей внутри интервала, ряд сходится абсолютно, для точек x, лежащих вне него – расходится. Число R – радиус сходимости степенного ряда. Для
определения радиуса сходимости R
применяют признаки Даламбера и Коши
для модулей
членов ряда. Для определения R
используем признак Даламбера для
модулей:
|
5.
Пусть
члены ряда
непрерывная
невозрастающая функция, что
Из
рисунка (б) следует, что сумма площадей
всех прямоугольников равна
Пусть
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
18. Вычисление тройного интеграла Предположим, что пространственная область V, ограниченная замкнутой поверхностью S, обладает следующими свойствами: 1. Всякая прямая, параллельная оси OZ, проведенная через внутреннюю точку области V , пересекает поверхность S в двух точках. 2. Вся область V проектируется на плоскость ХОУ в правильную область D. 3. Всякая часть области V, отсеченная плоскостью, параллельной и любой из координатных плоскостей, также обладает свойствами 1, 2. Область V, обладающую указанными свойствами, будем называть правильной трехмерной областью. Пример – эллипсоид, тетраэдр.
Пусть
поверхность, ограничивающая область
V
снизу, имеет уравнение:
Свойства тройного интеграла:
1.
Если область V
разбита на области
2.
Если m
и М
– наименьшее и наибольшее значение
функции
3. 4.
Если в тройном интеграле положить
|
12.
Рассмотрим
в плоскости XOY
замкнутую область D,
ограниченную линией L.
Пусть в области D
задана непрерывная функция
Теорема
1.
Если
Теорема
2.
Двойной интеграл от суммы двух функций
Теорема
3.
Постоянный множитель можно вынести
за знак двойного интеграла:
Теорема
4.
Если область D
разбита на две области
Теорема
5.
(теорема
о среднем). Теорема
6.
Если
|
17. Понятие тройного интеграла
Пусть
в пространстве задана область V,
ограниченная замкнутой поверхностью
S.
Пусть в области V
и на ее границе определена непрерывная
функция
11.
Имеется
формула
Тейлора
для функции
|
16.
Пусть
в полярной системе координат
Пусть
в области D
задана непрерывная функция
Из
теоремы существования двойных
интегралов следует, что при
Обозначим
через
Если
площадка
Теперь
пусть
|
13.
Пусть область D
такова, что всякая прямая, параллельна,
одной из координатных осей, например,
оси
Пусть
Пусть
область D
такова, что одна из функций
Теорема.
Двойной интеграл от непрерывной
функции
Замечание
1.
Пусть правильная в направлении оси
OX
область D
ограниченная линиями
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.
Пусть
задана бесконечная последовательность
чисел
Теорема 1. Если сходится ряд, полученный из данного ряда (1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, полученный из данного ряда отбрасыванием нескольких членов.
Теорема
2.
Если ряд
Теорема
3.
Если ряды
Теорема. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n. Пусть
ряд
|
23. Теоремы умножения вероятностей
Произведением
событий А и B называется событие C
состоящее осуществлением и события
A и события B. C=AB. Условной вероятностью
события A относительно события B
Пример.
В урне 6 белых и 5 черных шаров на удачу
вынимают последовательно 2 шара найти
вероятность того что второй шар черный,
если 1 извлеченный шар белый. Пусть
событие
Теорема:
Вероятность произведения двух событий
равна произведению вероятности одного
из них на условную вероятность другого
при условии, что первое событие
произошло:
1.
На пяти карточках записаны буквы О Л
О В О, карточки извлекают на удачу
извлекают по одной и выкладывают в
линию. Найти вероятность того, что
получится данное слово. Событие A.
2. Среди 17 студентов группы, в которой 9 юношей производится розыгрыш 7 билетов лотереи, причем каждый студент может выбрать только один билет. Какова вероятность того, что среди обладателей билетов будет 4 девушки.
Теорема:
Вероятность произведения двух
независимых событий равно произведению
их вероятностей
|
15. Якобиан преобразования имеет вид, где
|
24. Вероятность появления хотя бы одного события
2
стрелка стреляют по мишени вероятность
попадания
Теорема:
Вероятность появления хотя бы одного
из событий
|
21. Элементы комбинаторики
Комбинаторика
рассматривает подсчет количества
способов, выбора определенного
количества элементов по определенным
правилам. Различают размещения
перестановки и сочетания. Размещениями
называют комбинации, составленные из
m элементов взятых из общего количества
n, которое обличается либо составом
элементов, либо порядком. Число
размещений
22. Геометрическая и статическая вероятности. Классическое определение вероятности дает возможность рассматривать события, которые распадаются на конечное число равновероятных случаях. если количество равновероятных исходов большое, то используют геометрическую вероятность. Пусть имеется отрезок длиной L, внутри которого имеется отрезок длиной l. На отрезок 4 ставится точка. Считается, что вероятность попадания на отрезок l пропорциональна длине отрезка 4. Тогда вероятность попадания этой точки на отрезке l P(A)=l/L. Иногда удобно использовать отношение площадей P(A)=S^'/S. Относительная частота это отношение числа появления события A m к общему числу испытаний n (…m/n). Если число испытаний n неограниченно возрастает, то частость стремится к вероятности события |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27. Формула Байеса
Пусть
имеется полная группа гипотез
вероятности, которых
Исходя
из того, что событие А произошло,
необходимо переоценить приятности
гипотез, то есть определить условную
вероятность
|
26. Формула полной вероятности
Пример:
на конвейер поступает продукция 3
станков. Причем 50% продукции изготавливает
первый станок, 30% второй станок и 20%
третий. Для 1 станка брак составляет
2%, для 2 3% и для 3 5%. Найти вероятность
того, что наудачу взятая деталь будет
доброкачественная. Событие A взятая
деталь – доброкачественная. Вероятности
изготовления стандартной детали
Теорема.
Вероятность события А, которое может
наступить при появлении одной из
гипотез
|
27. Событие А называется независимым в данной системе испытаний, если вероятность этого события в каждом из них не зависит от исходов других испытаний. Тогда считаем, что вероятность появления события А в каждом испытании постоянна и равна p.
Определим
вероятность
|
25. Суммой или объединением A и B называется событие C, состоящее в наступлении события A, или события B или событий A и B вместе: C=A+B.
Теорема.
Вероятность
суммы конечного числа несовместных
событий равна сумме их вероятностей.
Докажем для двух событий. Пусть из
общего числа n
случаев событию A
благоприятствует k
случаев, а событию
Следствие1: Сумма вероятностей событий, образующих полную группу, равна 1.
Следствие2:
Сумма
вероятностей противоположных событий
равна 1,
|
29. Локальная теорема Лапласа. Формула Пуассона
Если
число испытаний n
велико (n
> 20), то вычисления по формуле Бернулли
громоздкие. Например,
Очевидно,
что
Пример.
Вероятность поражения цели стрелком
при одиночном выстреле
Вероятность малая, поскольку ровно 20 раз. Почти достоверное событие - около 20 раз.
Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30. Интегральная теорема Лапласа
Часто
необходимо найти вероятность того,
что число появлений события А
заключено в интервале
Следствие.
Если вероятность р
наступления события А
– постоянна
|
31. Понятие случайной величины. Закон распределения дискретной случайной величины
На
практике часто встречаются величины,
которые могут принимать некоторые
значения, но нельзя достоверно
предсказать, какое именно значение
каждая из них примет в рассмотренном
испытании.
Например,
число мальчиков, родившихся в Белгороде
завтра, может быть различным:
Непрерывной
называют случайную величину, которая
может принимать все значения из
некоторого конечного (или бесконечного)
промежутка. Пусть
Х
– дискретная случайная величина,
возможными и единственными значениями
которой являются х1,
х2,
х3,…,
хn.
Обозначим через
Если
множество xi – бесконечно, то ряд
|
32.33. Математическое ожидание дискретной случайной величины и его свойства Закон распределения полностью описывает случайную величину, однако иногда выгоднее пользоваться числами, которые описывают случайную величину суммарно – это числовые характеристики величин. Рассмотрим математическое ожидание.
Математическим
ожиданием дискретной случайной
величины называют сумму произведений
всех ее возможных значений на их
вероятности.
Пусть дискретная случайная величина
принимает значения
1.
Математическое ожидание постоянной
величины равно самой постоянной, т.е
С
имеет одно значение, равное С, с
вероятностью
2.
Случайные
величины X
и Y
называют независимыми,
если закон распределения одной из них
не зависит от того, какие значения
принимает другая. Произведение
3.
Составим
значения, которые могут принимать
4.
Теорема.
М(Х)
числа появлений событий А
в n
независимых испытаниях равно
произведению числа испытаний на
вероятность появления события в одном
испытании p.
Иначе, М(Х)
биноминального распределения равно
|
34. Дисперсия случайной дискретной величины и ее свойства. Легко указать случайные величины, имеющие одинаковые значения математических ожиданий, но различные возможные значения, например:
Теорема.
Математическое ожидание отклонения
равно нулю. Действительно,
Дисперсией
(рассеянием)
дискретных случайных величин называется
математическое ожидание квадрата
отклонения случайной величины от ее
математического ожидания:
Получаем:
Свойства дисперсии
1.
Дисперсия
постоянной величины равной нулю.
2.
Постоянный
множитель можно выносить за знак
дисперсии, возводя его в квадрат:
3.
Дисперсия
суммы двух независимых случайных
величин равна сумме дисперсий этих
величин
4.
Теорема.
Дисперсия числа появлений событий А
в n
независимых испытаниях, в каждом из
которых вероятность появления события
А
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
35.
Дискретная случайная величина может
быть задана перечислением всех ее
возможных значений и их вероятностей
– законом распределения. Но его нельзя
использовать для задания непрерывных
случайных величин. Необходим общий
способ задания случайных величин -
это функция распределения вероятностей
случайных величин. Пусть x
– действительное число. Вероятность
того, что случайная величина Х
примет значение, меньше x,
т.е.
Добавим более четкое определение непрерывной случайной величины – случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Свойства F(x)
Следствие
1.
Вероятность того, что
Следствие
2.
Вероятность того, что случайная
величина Х
примет одно определенное значение
равна 0.
Докажем.
Если
Следствие.
Если значения непрерывной случайной
величины расположены на всей числовой
оси, то
|
36. Плотность распределения вероятностей непрерывной случайной величины и ее свойства
Непрерывную
случайную величину можно задать
функцией распределения, однако можно
использовать и плотностью распределения.
Плотностью распределения вероятностей
непрерывной случайной величины Х
называют производную от функции
распределения:
Теорема.
Вероятность того, что непрерывная
случайная величина Х
примет значение, принадлежащее
интервалу
Доказательство:
Если
известна функция распределения, то
1.
2.
Вероятностный
смысл
37. Числовые характеристики непрерывных случайных величин Распространим определение числовых характеристик дискретных случайных величин на величины непрерывные.
Математическое
ожидание
Аналогично:
|
38. Нормальное распределение
Нормальным
распределением называется распределение
вероятностей непрерывных случайных
величин, которые описываются плотностью
распределения
|
39. Вероятности попадания в заданный интервал и заданного отклонения для нормальной случайной величины.
функция Лапласа. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Вычисление вероятности заданного отклонения
Часто
требуется найти вероятность того, что
отклонение нормально распределенной
случайной величины Х от математического
ожидания по модулю меньше данного
Правило
3x
сигм: если
|
40. Задачи математической статистики. Вариационный ряд Первая задача статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или экспериментов. Вторая задача – разработать методы анализа статистических данных в зависимости от целей исследования: а) оценка неизвестной вероятности события, известной функции распределения, параметров распределения, вид которого известен и т.д. б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен. Для исследования какого-либо признака из генеральной совокупности (всех объектов) извлекают выборку – случайно отображенные объекты. Вариационный ряд Рассмотрим пример. Токарь изготавливал в течение 10 дней следующее количество деталей: 5,6,5,7,7,7,8,5,6,5. Ранжируем эту выборку – разобьем на группы: 5,5,5,5 6,6 7,7,7 8 4 раза 2 раза 3 раза 1 раз. При ранжировании группы располагаются в порядке возрастания. Значение каждой группы называется вариантой. Число повторений в каждой группе называется частотой варианты. Полученную таблицу называют вариационным рядом.
В общем виде
Графическое
изображение вариационного ряда –
полигон.
Для непрерывного признака весь
интервал, в котором заключены все
наблюдаемые значения признака,
разбивают на несколько частичных
интервалов длиной h и находят для
каждого частичного интервала
Гистограммой
относительных частот называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
41. 42.Точечные оценки
Вариационный
ряд характеризует
случайную величину, но не в полной
мере, поэтому используются характеристики,
аналогичные теоретическим – М(х),
D(х)
и т.д. Эти числовые характеристики
подсчитываются на основании выборки
и называются точечными оценками (т.к.
являются числами). Точечной
оценкой
характеристики
называется некоторая функция *
результатов наблюдений, значение
которой принимают за приближение этой
характеристики:
1.
Несмещенность оценки: точечная оценка
называется несмещенной, если ее
математическое ожидание равно
оценивающему параметру:
2.
Состоятельность: точечная оценка
называется состоятельной, если она
при
3. Эффективность: точечная оценка считается эффективной, если она имеет (при заданном n) наименьшую дисперсию. Основные точечные оценки
1.
Выборочная средняя:
Выборочная
средняя
2.
Выборочная дисперсия:
3.
Начальные и центральные моменты k-го
порядка. Начальный момент k-го
порядка:
|
43. Интервальные оценки для генеральной средней
При
выборке малого объема точечная оценка
может сильно отличаться от оцениваемого
параметра, поэтому широко используют
интервальные оценки. Интервальной
называют оценку, которая определяется
двумя числами – концами интервала.
Доверительной вероятностью (надежностью)
называется вероятность ,
с которой осуществляется неравенство
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Интервальные
оценки для генеральной средней с
известным .
Пусть
известно среднее квадратическое
отклонение
генеральной совокупности с нормальным
законом распределения. Требуется
оценить неизвестное математическое
ожидание, а
по
выборочной средней
(
Тогда
по следствию интегральной теоремы
Лапласа имеем:
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Интервальная
оценка для генеральной средней с
неизвестным .
Пусть
признак Х
генеральной совокупности распределен
нормально, причем среднее квадратическое
отклонение
неизвестно. Требуется оценить
неизвестное математическое ожидание
а
по
выборочной средней
|
44. Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли
Пусть
из генеральной совокупности,
распределенной по нормальному закону
Случайная
величина
Тогда:
из
Если
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
плоскостью
,
плоскостью
 и цилиндрической поверхностью,
направляющей для которой служит
граница области D,
а образующие параллельные оси
и цилиндрической поверхностью,
направляющей для которой служит
граница области D,
а образующие параллельные оси
 ,равен
,равен
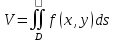
 .
Очевидно,
что
.
Очевидно,
что
 .
.
 ,
а снизу – поверхностью
,
а снизу – поверхностью
 причем проекцией обеих поверхностей
на плоскость
причем проекцией обеих поверхностей
на плоскость
 является область D,
то объем этого тела равен разности
объемов двух цилиндроидов:.
является область D,
то объем этого тела равен разности
объемов двух цилиндроидов:. .
Формула верна для любых непрерывных
функций
.
Формула верна для любых непрерывных
функций
 ,
для которых
,
для которых

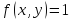 по области D,
то эта сумма равна площади
по области D,
то эта сумма равна площади
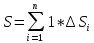 .
Переходя к пределу, получим:
.
Переходя к пределу, получим:
 .
Если область – правильная, то имеем
.
Если область – правильная, то имеем
 – формула, рассмотренная ранее.
– формула, рассмотренная ранее.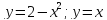 .
Координаты точек пересечения:
.
Координаты точек пересечения:

 (2) и
(2) и
 (3).
(3). и
ряд (3) сходится, то сходится и ряд (2).
и
ряд (3) сходится, то сходится и ряд (2). сумма рядов. Из
сумма рядов. Из
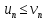 следует, что
следует, что
 Т.к. ряд (3) сходится, то
Т.к. ряд (3) сходится, то
 .
Т.к. члены рядов положительны, то
.
Т.к. члены рядов положительны, то
 Доказали, что частичные суммы
Доказали, что частичные суммы
 возрастают и ограничены, значит, они
имеют предел:
возрастают и ограничены, значит, они
имеют предел:

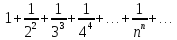 сходится,
т.к. его члены меньше соответствующих
членов ряда.
сходится,
т.к. его члены меньше соответствующих
членов ряда.
 Последний ряд сходится, т.к. начиная
со второго члена - это геометрическая
прогрессия с
Последний ряд сходится, т.к. начиная
со второго члена - это геометрическая
прогрессия с

 и ряд (3) расходится, то и ряд (2) расходится.
Из условия
и ряд (3) расходится, то и ряд (2) расходится.
Из условия
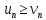 следует, что
следует, что
 (положительный ряд). Т.к. ряд (3) расходится,
то
(положительный ряд). Т.к. ряд (3) расходится,
то
 ,
тогда из
,
тогда из
 следует, что,
следует, что,
 т.е. ряд (2) расходится.
т.е. ряд (2) расходится. расходится,
т.к его члены начиная со второго, больше
соответствующих членов гармонического
ряда
расходится,
т.к его члены начиная со второго, больше
соответствующих членов гармонического
ряда
 ,
который расходится.
,
который расходится. то ряды (2) и (3) сходятся или расходятся
одновременно.
то ряды (2) и (3) сходятся или расходятся
одновременно. где
где
 - положительны.
- положительны. члены таковы, что
члены таковы, что
 и
и
 ,
то ряд (1) сходится, его сумма положительна
и не превосходит
,
то ряд (1) сходится, его сумма положительна
и не превосходит
 .
Рассмотрим сумму
.
Рассмотрим сумму
 первых членов ряда (1):
первых членов ряда (1):
 .
Из (2) следует, что
.
Из (2) следует, что
 и возрастает с увеличением m. Запишем
и возрастает с увеличением m. Запишем
 В силу (2) каждая скобка положительна.
В результате вычитаний получим число,
меньше
В силу (2) каждая скобка положительна.
В результате вычитаний получим число,
меньше
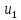 ,
т.е.
,
т.е.
 .
.
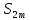 возрастает и ограниченна сверху
возрастает и ограниченна сверху
 поэтому имеет предел S:
поэтому имеет предел S:
 .
Рассмотрим нечетные суммы:
.
Рассмотрим нечетные суммы:
 сходится. Замечание. Теорема Лейбница
справедлива, если (2) выполняется,
начиная с некоторого N.
сходится. Замечание. Теорема Лейбница
справедлива, если (2) выполняется,
начиная с некоторого N.
 отношение
отношение
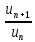 при
при
 имеет конечный придел
имеет конечный придел
 ,
т.е.
,
т.е.
 ,
то ряд сходится в случаи
,
то ряд сходится в случаи
 ряд расходится при.
ряд расходится при.
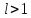 При
При
 теорема не дает ответа о сходимости
ряда.
теорема не дает ответа о сходимости
ряда.
 Рассмотрим число
Рассмотрим число
 .
По определению предела
.
По определению предела
 начиная с номера
начиная с номера
 отсюда
отсюда
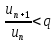 .
Запишем последнее неравенство для
.
Запишем последнее неравенство для
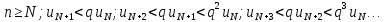 Рассмотрим
два ряда:
Рассмотрим
два ряда:
 (1) и
(1) и
 Ряд
Ряд
 – геометрическая прогрессия с
– геометрическая прогрессия с
 – сходится. Члены ряда (1), начиная с
– сходится. Члены ряда (1), начиная с
 ,
меньше членов ряда
,
меньше членов ряда
 поэтому ряд (1) сходится на основании
признака сравнения.
поэтому ряд (1) сходится на основании
признака сравнения. .
Тогда из
.
Тогда из
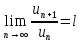 ,
,
 следует, что
следует, что
 для
для
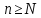 .
Но это означает, что члены ряда
возрастают и
.
Но это означает, что члены ряда
возрастают и
 не стремится к 0, поэтому ряд расходится.
не стремится к 0, поэтому ряд расходится. ,
то ряд расходится.
,
то ряд расходится. ,
но
,
но
 ,
начиная с
,
начиная с
 ,
то ряд расходится.
,
то ряд расходится. (1) величина
(1) величина
 имеет конечный предел
имеет конечный предел

 .
Рассмотрим
.
Рассмотрим
 .
Начиная с
.
Начиная с
 .
Рассмотрим два ряда:
.
Рассмотрим два ряда:
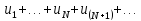 (1) и
(1) и
 Ряд
Ряд
 сходится – геометрическая прогрессия
с
сходится – геометрическая прогрессия
с
 Члены ряда (1), начиная с
Члены ряда (1), начиная с
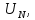 меньше членов ряда
меньше членов ряда
 ряд (1) сходится.
ряд (1) сходится.
 ,
тогда
,
тогда
 начиная с
начиная с
 или
или
 – ряд расходится, т.к.
– ряд расходится, т.к.
 не стремится к нулю.
не стремится к нулю.
 то требуется дальнейшие исследования.
то требуется дальнейшие исследования. однако ряд расходится.
однако ряд расходится. ,
но ряд сходится, т.к. члены ряда, начиная
со второго, меньше членов сходящего
ряда
,
но ряд сходится, т.к. члены ряда, начиная
со второго, меньше членов сходящего
ряда
 .
. .
События A
и B
называются несовместными, если их
совместное наступление невозможно.
События
.
События A
и B
называются несовместными, если их
совместное наступление невозможно.
События
 образуют полную группу, если они
попарно не совместны и в результате
испытания наступит одно и только одно
событие.
образуют полную группу, если они
попарно не совместны и в результате
испытания наступит одно и только одно
событие. называется абсолютно сходящимся, если
сходится ряд, составленный из абсолютных
величин его членов
называется абсолютно сходящимся, если
сходится ряд, составленный из абсолютных
величин его членов
 .
Если ряд (1) сходится, а ряд (2) расходится,
то знакопеременный ряд сходится
условно.
.
Если ряд (1) сходится, а ряд (2) расходится,
то знакопеременный ряд сходится
условно.
 - положительные и отрицательные.
- положительные и отрицательные. (1)
таков, что ряд из модулей
(1)
таков, что ряд из модулей (2)
сходится, то и данный ряд сходится.
(2)
сходится, то и данный ряд сходится. - суммы первых n
членов рядов (1) и (2).
- суммы первых n
членов рядов (1) и (2). - сумма положительных членов,
- сумма положительных членов,
 сумма модулей отрицательных членов,
тогда
сумма модулей отрицательных членов,
тогда
 и
и
 .
По условию
.
По условию
 имеет предел
имеет предел
 – положительные возрастающие величины,
меньшие
– положительные возрастающие величины,
меньшие
 ,
поэтому они имеют пределы
,
поэтому они имеют пределы
 ,
тогда и
,
тогда и
 имеет предел
имеет предел
 ,
т.е. (1) – сходится. Отметим следующие
свойства абсолютно и условно сходящихся
рядов.
,
т.е. (1) – сходится. Отметим следующие
свойства абсолютно и условно сходящихся
рядов. называется функциональным, если его
члены являются функциями от X:
называется функциональным, если его
члены являются функциями от X:
 .
Давая x
определенные числовые значения,
получим различные числовые ряды,
которые могут сходиться и расходиться.
Совокупность тех значений x,
при которых функциональный ряд
сходится, называется областью
сходимости ряда.
В области сходимости ряда его сумма
является функцией
.
Давая x
определенные числовые значения,
получим различные числовые ряды,
которые могут сходиться и расходиться.
Совокупность тех значений x,
при которых функциональный ряд
сходится, называется областью
сходимости ряда.
В области сходимости ряда его сумма
является функцией
 .
. .
Этот ряд сходится при
.
Этот ряд сходится при
 (убывающая геометрическая прогрессия).
Очевидно,
(убывающая геометрическая прогрессия).
Очевидно,
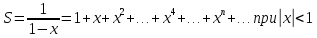 .
Пусть
.
Пусть
 – сумма первых n
членов ряда (1). Если этот ряд сходится
и его сумма равна
– сумма первых n
членов ряда (1). Если этот ряд сходится
и его сумма равна
 остаток ряда. Для всех х
в области сходимости ряда
остаток ряда. Для всех х
в области сходимости ряда
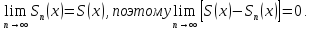
 имеет интервал сходимости
имеет интервал сходимости
 ,
то ряд
,
то ряд
 ,
полученный почленным дифференцированием
ряда (1), имеет тот же интервал сходимости
,
полученный почленным дифференцированием
ряда (1), имеет тот же интервал сходимости
 ,
т.е. внутри интервала сходимости
производная от суммы ряда равна сумме
производных от членов ряда.
,
т.е. внутри интервала сходимости
производная от суммы ряда равна сумме
производных от членов ряда. если
если
 принадлежат интервалу сходимости
принадлежат интервалу сходимости
 .
Т.е. если пределы интегрирования лежат
внутри интервала сходимости степенного
ряда, то интеграл от суммы ряда равен
сумме интегралов от членов ряда
.
Т.е. если пределы интегрирования лежат
внутри интервала сходимости степенного
ряда, то интеграл от суммы ряда равен
сумме интегралов от членов ряда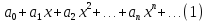 ,
где
,
где
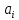 –числа
– коэффициенты ряда.
–числа
– коэффициенты ряда. ,
то он абсолютно сходится при всяком
значении x,
для которого
,
то он абсолютно сходится при всяком
значении x,
для которого
 .
. ,
то он расходится при всяком x,
для которого
,
то он расходится при всяком x,
для которого
 .
. – точка сходимости, то весь интервал
– точка сходимости, то весь интервал
 заполнен точками абсолютной сходимости,
т.е. существует число R,
такое что при всех х
таких, что
заполнен точками абсолютной сходимости,
т.е. существует число R,
такое что при всех х
таких, что
 - степенной ряд сходится, а при
- степенной ряд сходится, а при
 – расходится.
– расходится. .
.
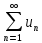 положительны и не возрастают, т.е.
положительны и не возрастают, т.е.
 и пусть
и пусть
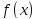 -
такая
-
такая
 .
Тогда ряд
.
Тогда ряд
 и несобственный интеграл
и несобственный интеграл
 сходятся или расходятся одновременно.
Построим графики членов ряда: Из
графика (а) следует, что площади
прямоугольников равны
сходятся или расходятся одновременно.
Построим графики членов ряда: Из
графика (а) следует, что площади
прямоугольников равны
 и т.д. и
и т.д. и
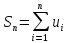 .
С другой стороны, площадь области,
ограниченной кривой
.
С другой стороны, площадь области,
ограниченной кривой
 и прямыми
и прямыми
 равна
равна
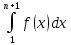 ,
поэтому
,
поэтому


 .
Предположим, что
.
Предположим, что
 остается ограниченной
остается ограниченной
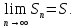
 расходится, тогда
расходится, тогда неограниченно возрастает при увеличении
n.
Тогда (из неравенства (1))
неограниченно возрастает при увеличении
n.
Тогда (из неравенства (1))
 тоже неограниченно возрастает, т.е.
ряд расходится. Пример.
Ряд Дирихле:
тоже неограниченно возрастает, т.е.
ряд расходится. Пример.
Ряд Дирихле:

 ,
а сверху –
,
а сверху –
 .
Пусть область D
– проекция области V
на плоскость ХОУ
–
ограниченна линиями:
.
Пусть область D
– проекция области V
на плоскость ХОУ
–
ограниченна линиями:
 .
Введем понятие трехкратного интеграла
от функции
.
Введем понятие трехкратного интеграла
от функции
 по области V:
по области V:
 .
В результате интегрирования по z
в квадратных скобках, получится функция
от х
и у.
Далее вычисляем двойной интеграл по
области D
. Теорема.
Тройной интеграл от
.
В результате интегрирования по z
в квадратных скобках, получится функция
от х
и у.
Далее вычисляем двойной интеграл по
области D
. Теорема.
Тройной интеграл от
 по правильной области равен трехкратному
интегралу по этой же области, т.е.
по правильной области равен трехкратному
интегралу по этой же области, т.е.
 .
. и
и
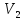 плоскостью, параллельной какой – либо
из плоскостей координат, то тройной
интеграл по области V
равен сумме тройных интегралов по
областям
плоскостью, параллельной какой – либо
из плоскостей координат, то тройной
интеграл по области V
равен сумме тройных интегралов по
областям
 .
.
 в
области V,
то
в
области V,
то
 ,
где V
– объем данной области.
,
где V
– объем данной области.
 ,
где V
– объем области.
,
где V
– объем области.
 .
. .
Разобьем область D
на n
частей:
.
Разобьем область D
на n
частей:
 называемых площадками. Через
называемых площадками. Через
 обозначим и площади площадок. В каждой
из площадок возьмем точку
обозначим и площади площадок. В каждой
из площадок возьмем точку
 .
Обозначим через
.
Обозначим через
 значения функции в выбранных точках
и составим сумму произведении вида
значения функции в выбранных точках
и составим сумму произведении вида
 .
Эта сумма называется интегральной
суммой для функции
.
Эта сумма называется интегральной
суммой для функции
 – объем цилиндра, построенного на
– объем цилиндра, построенного на
 как на основании с высотой
как на основании с высотой
 .
. непрерывна в замкнутой области D,
то существует предел последовательности
(2) интегральных сумм (1), если max
диаметр площадок
непрерывна в замкнутой области D,
то существует предел последовательности
(2) интегральных сумм (1), если max
диаметр площадок
 ,
который не зависит ни от способов
разбиения области D,
ни от выбора точек
,
который не зависит ни от способов
разбиения области D,
ни от выбора точек
 .
Этот предел называется двойным
интегралом от функции
.
Этот предел называется двойным
интегралом от функции
 по области D
и обозначается:
по области D
и обозначается:

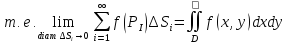 ,
D
– область интегрирования. Если
,
D
– область интегрирования. Если
 – объему тела, ограниченного поверхностью
– объему тела, ограниченного поверхностью
 ,
плоскостью
,
плоскостью
 и цилиндрической поверхностью,
образующие которой параллельны
и цилиндрической поверхностью,
образующие которой параллельны
 ,
а направляющей служит граница области
D.
,
а направляющей служит граница области
D. по области D
равен сумме двойных интегралов по
области D
от каждой из функций в отдельности.
по области D
равен сумме двойных интегралов по
области D
от каждой из функций в отдельности.

 без общих внутренних точек и функция.
без общих внутренних точек и функция.
 во всех точках области D
удовлетворяет неравенствам
во всех точках области D
удовлетворяет неравенствам
 ,
где S
– площадь области D.
,
где S
– площадь области D. (если
(если – то можно рассматривать плотность
распределения вещества в области V).
Разобьем область V
на n
областей
– то можно рассматривать плотность
распределения вещества в области V).
Разобьем область V
на n
областей
 произвольным образом, причем
произвольным образом, причем
 – это и объем этой области. В пределах
каждой частичной области
– это и объем этой области. В пределах
каждой частичной области
 выберем произвольную точку
выберем произвольную точку
 и составим интегральную сумму
и составим интегральную сумму
 .
Перейдем к пределу, т.е.
.
Перейдем к пределу, т.е.
 ,
чтобы и
,
чтобы и
 ,
тогда для непрерывной функции
,
тогда для непрерывной функции
 существует
предел интегральных сумм, который не
зависит ни от способа разбиения
области, ни от выбора точек
существует
предел интегральных сумм, который не
зависит ни от способа разбиения
области, ни от выбора точек
 Это предел
обозначается
символом
Это предел
обозначается
символом
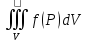 и
называется тройным интегралом, т.е.
и
называется тройным интегралом, т.е.
 .
Если считать
.
Если считать
 – объемной плотностью распределения
вещества в области V,
то тройной интеграл даст массу вещества
в области V.
– объемной плотностью распределения
вещества в области V,
то тройной интеграл даст массу вещества
в области V. ,
имеющий производные до
,
имеющий производные до
 включительно, в окрестности точки
включительно, в окрестности точки
 Если
Если
 имеет производные всех порядков в
окрестности точки
имеет производные всех порядков в
окрестности точки
 ,
то в формуле Тейлора число n
можно брать сколь угодно большим.
Допустим, что
,
то в формуле Тейлора число n
можно брать сколь угодно большим.
Допустим, что
 ,
тогда, переходя в формуле Тейлора к
пределу при
,
тогда, переходя в формуле Тейлора к
пределу при
 ,
получим справа бесконечный ряд,
Тейлора:
,
получим справа бесконечный ряд,
Тейлора:
 .
Если в формуле ряда Тейлора положить
.
Если в формуле ряда Тейлора положить
 ,
то получим ряд
Маклорена:
,
то получим ряд
Маклорена:
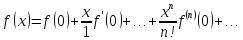 .
Для каждой элементарной функции
существуют
.
Для каждой элементарной функции
существуют
 ,
такие, что в интервале
,
такие, что в интервале
 она разлагается в ряд Тейлора
(или Маклорена).
она разлагается в ряд Тейлора
(или Маклорена). задана такая область D,
что каждый луч, проходящий через
внутреннюю точку области, пересекает
границу области не более чем в двух
точках. D
ограничена кривыми
задана такая область D,
что каждый луч, проходящий через
внутреннюю точку области, пересекает
границу области не более чем в двух
точках. D
ограничена кривыми
 .
Такую
область называют правильной.
.
Такую
область называют правильной. Разобьем D
на площадки
Разобьем D
на площадки
 и составим интегральную сумму
и составим интегральную сумму

 существует предел V
интегральной суммы:
существует предел V
интегральной суммы:
 Т.к. предел интегральной суммы не
зависит от способа разбиения D,
то разобьем D
с помощью лучей
Т.к. предел интегральной суммы не
зависит от способа разбиения D,
то разобьем D
с помощью лучей
 и
концентрических окружностей:
и
концентрических окружностей:


 площадку, ограниченную линиями
площадку, ограниченную линиями

 пересекается границей или не лежит в
D,
то их не учитываем
пересекается границей или не лежит в
D,
то их не учитываем
 .
Интегральная сумма
.
Интегральная сумма
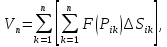 где
где
 – произвольная точка площадки
– произвольная точка площадки
 .
Найдем площадь
.
Найдем площадь
 .
Она равна разности площадей двух
секторов:
ощадь
.
Она равна разности площадей двух
секторов:
ощадь
 .
Тогда интегральная сумма:
.
Тогда интегральная сумма:


 .
Предположим, что
.
Предположим, что
 .
.
 – формула для вычисления двойного
интеграла в полярных координатах.
Если область D
является правильной в полярных
координатах, то
– формула для вычисления двойного
интеграла в полярных координатах.
Если область D
является правильной в полярных
координатах, то
 .
. и проходящая через внутреннюю точку
области D пересекает границу области
в двух точках. Предположим, что область
ограничена линиями:
и проходящая через внутреннюю точку
области D пересекает границу области
в двух точках. Предположим, что область
ограничена линиями:
 причем
причем
 и функции
и функции
 и
и
 непрерывны на отрезке
непрерывны на отрезке
 .
Такая область называется правильной
в направлении оси
.
Такая область называется правильной
в направлении оси
 .
Аналогично, определяется область,
правильная в направлении оси
.
Аналогично, определяется область,
правильная в направлении оси
 .
Область, правильную как в направлении
оси
.
Область, правильную как в направлении
оси
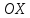 .
так и оси
.
так и оси
 ,
называют правильной.
,
называют правильной.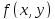 непрерывна в области D.
Рассмотрим
непрерывна в области D.
Рассмотрим
 ,
который будем называть двукратным
интегралом от
,
который будем называть двукратным
интегралом от
 по области D.
В этом выражении сначала вычисляется
определенный интеграл, стоящий в
скобках, при этом считаем, что
по области D.
В этом выражении сначала вычисляется
определенный интеграл, стоящий в
скобках, при этом считаем, что
 получаем функцию
получаем функцию
 далее вычисляем определенный интеграл
далее вычисляем определенный интеграл
 ,
который равен постоянному числу.
,
который равен постоянному числу. не может быть задана одним аналитическим
выражением на всем участке
не может быть задана одним аналитическим
выражением на всем участке

 по правильной области D
равен двукратному интегралу от этой
функции по области D:
по правильной области D
равен двукратному интегралу от этой
функции по области D:


 .
Для вычисления двойного интеграла
его надо представить в виде двукратного.
В каждом конкретном случаи надо выбрать
формулу (1) или (2) в зависимости от вида
области и подынтегральной функции
.
Для вычисления двойного интеграла
его надо представить в виде двукратного.
В каждом конкретном случаи надо выбрать
формулу (1) или (2) в зависимости от вида
области и подынтегральной функции
 .
. .
Выражение
.
Выражение
 (1) называется числовым
рядом.
Числа
(1) называется числовым
рядом.
Числа
 ,
называются членами ряда. Сумма конечного
числа n
первых членов ряда называется
n-ой
частичной
суммой ряда:
,
называются членами ряда. Сумма конечного
числа n
первых членов ряда называется
n-ой
частичной
суммой ряда:
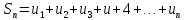 Рассмотрим частичные суммы:
Рассмотрим частичные суммы:
 .
Если существует конечный предел
.
Если существует конечный предел
 ,
то его называют
суммой ряда (1)
и говорят, что
ряд сходится.
Если
,
то его называют
суммой ряда (1)
и говорят, что
ряд сходится.
Если
 не существует, то
ряд расходится и суммы не имеет.
не существует, то
ряд расходится и суммы не имеет.
 сходится и его сумма равна
S,
то ряд
сходится и его сумма равна
S,
то ряд
 тоже сходится и его сумма =Sc.
тоже сходится и его сумма =Sc. и
и
 сходятся и их суммы равны соответственно
сходятся и их суммы равны соответственно
 и
и
 ,
то ряды
,
то ряды
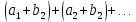 и
и
 тоже
сходятся и их суммы равны
тоже
сходятся и их суммы равны
 и
и
 соответственно.
соответственно.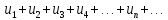 сходится, т.е.
сходится, т.е.
 – сумма ряда. Тогда
– сумма ряда. Тогда
 .
Вычтем из одного другое:
.
Вычтем из одного другое:
 Следствие.
Если
Следствие.
Если
 ,
то ряд расходится
,
то ряд расходится называется вероятность события A,
найденное в предположении, что событие
B уже произошло.
называется вероятность события A,
найденное в предположении, что событие
B уже произошло. событие B второй извлеченный шар
черный, тогда вероятность этого
события.
событие B второй извлеченный шар
черный, тогда вероятность этого
события.

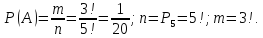



 Следовательно,
дифференциальный элемент в полярных
координатах будет равен
Следовательно,
дифференциальный элемент в полярных
координатах будет равен
 Пусть область интегрирования R
в полярных координатах определяется
следующим образом (рис 2)
Пусть область интегрирования R
в полярных координатах определяется
следующим образом (рис 2)
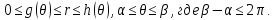 Тогда двойной интеграл в полярных
координатах описывается формулой
Тогда двойной интеграл в полярных
координатах описывается формулой
 Полученную область (рис 3) будем
называть полярным прямоугольником и
удовлетворяющую условиям
Полученную область (рис 3) будем
называть полярным прямоугольником и
удовлетворяющую условиям
 В этом случае формула замены переменных
в двойном интеграле имеет вид
В этом случае формула замены переменных
в двойном интеграле имеет вид


 соответственно. Найти вероятность
хотя бы одного попадания. Пусть событие
А это хотя бы одно попадание. Вероятность
этого события, что попал один
соответственно. Найти вероятность
хотя бы одного попадания. Пусть событие
А это хотя бы одно попадание. Вероятность
этого события, что попал один
 .
Рассмотрим событие противоположное
А:
.
Рассмотрим событие противоположное
А:
 .
Пусть в результате испытания могут
появиться n
независимых событий либо некоторые
из этих событий, либо не одного. Пусть
нам известны вероятности появления
каждого события
.
Пусть в результате испытания могут
появиться n
независимых событий либо некоторые
из этих событий, либо не одного. Пусть
нам известны вероятности появления
каждого события
 которые обозначим соответственно
обозначим. Мы хотим найти вероятность
появления хотя бы одного из этих
событий. Рассмотрим противоположное
событие, которое состоит в том, что не
произошло не одно из событий
которые обозначим соответственно
обозначим. Мы хотим найти вероятность
появления хотя бы одного из этих
событий. Рассмотрим противоположное
событие, которое состоит в том, что не
произошло не одно из событий
 .
Вероятность противоположного события
.
Вероятность противоположного события
 где
где
 вероятность
не появления
вероятность
не появления
 так как тема вероятностей противоположных
событий равна 1. Вероятность появления
хотя бы одного из событий
так как тема вероятностей противоположных
событий равна 1. Вероятность появления
хотя бы одного из событий

 равна разности между единицей и
произведением вероятностей
противоположных событий:
равна разности между единицей и
произведением вероятностей
противоположных событий: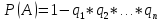 Следствие:
Если События
Следствие:
Если События
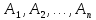 имеют одинаковую вероятность p,
то вероятность появления хотя бы
одного события
имеют одинаковую вероятность p,
то вероятность появления хотя бы
одного события

 ;
Перестановкой
называется размещение из m элементов
по n
;
Перестановкой
называется размещение из m элементов
по n
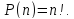 .
Сочетаниями называются комбинации
из n элементов по m, которые обличаются
хотя бы одним элементом (порядок
исследования не играет роли).
.
Сочетаниями называются комбинации
из n элементов по m, которые обличаются
хотя бы одним элементом (порядок
исследования не играет роли).
 ;
Размещениями
с повторениями называют упорядоченные
последовательности, составленные из
n
элементов по m
в каждом, где некоторые элементы могут
быть одинаковы.
;
Размещениями
с повторениями называют упорядоченные
последовательности, составленные из
n
элементов по m
в каждом, где некоторые элементы могут
быть одинаковы.
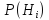 известны до опыта. Проводятся, в
результате, которого появляется
событие А. известно, что этому событию
А гипотезы предписывали определенные
условные вероятности
известны до опыта. Проводятся, в
результате, которого появляется
событие А. известно, что этому событию
А гипотезы предписывали определенные
условные вероятности
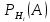 .
Определим какими стали вероятности
этих гипотез после опыта.
.
Определим какими стали вероятности
этих гипотез после опыта.
 .
.




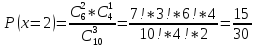

 .
вероятность того, что деталь изготовлена
первым станком равна 0,5, на втором 0,3,
на третьем 0,2.
.
вероятность того, что деталь изготовлена
первым станком равна 0,5, на втором 0,3,
на третьем 0,2.
 .
пусть событие А может произойти в
результате появления одного и только
одного. События
.
пусть событие А может произойти в
результате появления одного и только
одного. События
 из общей группы несовместных событий.
Тогда события
из общей группы несовместных событий.
Тогда события
 называются
гипотезами
называются
гипотезами
 равна сумме парных произведений
вероятностей всех гипотез на
соответствующие условные вероятности
события А
равна сумме парных произведений
вероятностей всех гипотез на
соответствующие условные вероятности
события А
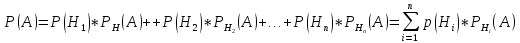 .
Доказательство:
событие А равносильно тому, что
произойдет
.
Доказательство:
событие А равносильно тому, что
произойдет
 .
.

 того, что при n
независимых испытаниях событие А,
имеющее одну и ту же вероятность р
для каждого отдельного испытания,
появится ровно k
раз, безразлично в какой последовательности.
Для каждого испытания имеется два
исхода: А
и
того, что при n
независимых испытаниях событие А,
имеющее одну и ту же вероятность р
для каждого отдельного испытания,
появится ровно k
раз, безразлично в какой последовательности.
Для каждого испытания имеется два
исхода: А
и
 .
Значит, если событие А
встречается k
раз, то
.
Значит, если событие А
встречается k
раз, то
 – (n
– k)
раз. Вероятность реализации такой
благоприятной серии:
– (n
– k)
раз. Вероятность реализации такой
благоприятной серии:
 Все благоприятные серии получаются
в результате выбора различных k
номеров из общего числа n,
т.е.
Все благоприятные серии получаются
в результате выбора различных k
номеров из общего числа n,
т.е.
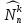 .
Напомним, что число сочетаний
.
Напомним, что число сочетаний
 .
Тогда по теореме сложения для
несовместных событий:
.
Тогда по теореме сложения для
несовместных событий:

 случаев. Тогда
случаев. Тогда
 ;
По условию события A
и B
несовместимы. Следовательно, ни один
из k
случаев, благоприятствующих A,
не благоприятствующих B.
Сумме
;
По условию события A
и B
несовместимы. Следовательно, ни один
из k
случаев, благоприятствующих A,
не благоприятствующих B.
Сумме
 благоприятствующим
благоприятствующим
 случаев из n,
поэтому
случаев из n,
поэтому
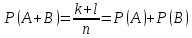 (доказательством является диаграмма
Виена).
(доказательством является диаграмма
Виена).
 .
Лаплас получил приближенную формулу:
.
Лаплас получил приближенную формулу:
 ,
где
,
где
 .
Функция
.
Функция
 табулированная, т.е. имеется таблица
значений функции.
табулированная, т.е. имеется таблица
значений функции. – функция четная.
– функция четная. .
Найти вероятность того, что из 100
выстрелов будет ровно 20 попаданий.
.
Найти вероятность того, что из 100
выстрелов будет ровно 20 попаданий. .
. (таблица 1), тогда
(таблица 1), тогда

 ,
но близка к нулю, а n
достаточно велико, причем
,
но близка к нулю, а n
достаточно велико, причем
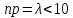 ,
то вероятность того, что в n
испытаниях событие A
наступит k
раз
,
то вероятность того, что в n
испытаниях событие A
наступит k
раз

 ,
т.е. число появлений события А
в n
испытаниях
не менее k1
и
не более
,
т.е. число появлений события А
в n
испытаниях
не менее k1
и
не более
 раз. Считаем, что вероятность появления
события А
раз. Считаем, что вероятность появления
события А .
Ответ
дает интегральная теорема Лапласа.
Вероятность того, что в n
независимых испытаниях, в каждом из
которых вероятность равна
.
Ответ
дает интегральная теорема Лапласа.
Вероятность того, что в n
независимых испытаниях, в каждом из
которых вероятность равна
 ,
событие наступит не менее k1
раз, и не более k2
раз, приблизительно равно
,
событие наступит не менее k1
раз, и не более k2
раз, приблизительно равно
 ,
где
,
где
 – функция Лапласа, которая табулирована;
– функция Лапласа, которая табулирована;
 .
Функция Лапласа
.
Функция Лапласа
 – нечетная:
– нечетная:
 ,
возрастающая, для
,
возрастающая, для
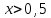 можно считать, что
можно считать, что
 .
. ,
а число испытаний достаточно велико,
то вероятность того, что в n
независимых испытаниях абсолютная
величина отклонения относительной
частоты события А
от его вероятности р
не превзойдет данного
,
а число испытаний достаточно велико,
то вероятность того, что в n
независимых испытаниях абсолютная
величина отклонения относительной
частоты события А
от его вероятности р
не превзойдет данного
 ,
находится по формуле
,
находится по формуле
 .
Т.к
.
Т.к
 ,
то
,
то
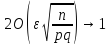 при
при
 В условиях Бернулли, как бы ни было
мало
В условиях Бернулли, как бы ни было
мало
 ,
с вероятностью, сколь угодно близкой
к 1, можно ожидать, что при
,
с вероятностью, сколь угодно близкой
к 1, можно ожидать, что при
 будет меньше
будет меньше
 (закон больших чисел в форме Бернулли).
(закон больших чисел в форме Бернулли). .
Или – дальность полета снаряда,
количество бракованных изделий в
партии и т.д. Это – случайные величины.
Случайной
величиной называется переменная,
которая может принимать те или иные
значения, причем для каждого испытания
она принимает единственное значение.
Случайные величины обозначают
заглавными буквами X,
Y,
Z,
значения случайных величин соответственно
малыми буквами.
Случайные величины делятся на дискретные
и непрерывные. Случайная величина
называется дискретной, если множество
ее значений конечно или счетное.
Например, стрельба по мишеням из орудия
до первого попадания (1,2,3,…, n,
).
Или – количество бракованных деталей
в партии из 30 изделий.
.
Или – дальность полета снаряда,
количество бракованных изделий в
партии и т.д. Это – случайные величины.
Случайной
величиной называется переменная,
которая может принимать те или иные
значения, причем для каждого испытания
она принимает единственное значение.
Случайные величины обозначают
заглавными буквами X,
Y,
Z,
значения случайных величин соответственно
малыми буквами.
Случайные величины делятся на дискретные
и непрерывные. Случайная величина
называется дискретной, если множество
ее значений конечно или счетное.
Например, стрельба по мишеням из орудия
до первого попадания (1,2,3,…, n,
).
Или – количество бракованных деталей
в партии из 30 изделий. вероятность этих значений, т.е. рi
есть вероятность того, что Х
принимает значения xi.
События Х
= хi
образует полную группу, поэтому
вероятность этих значений, т.е. рi
есть вероятность того, что Х
принимает значения xi.
События Х
= хi
образует полную группу, поэтому
 Закон распределения дискретных
случайных величин – соответствие
между всеми значениями дискретных
случайных величин и их вероятностями.
Обычно его записывают в виде таблицы:
Закон распределения дискретных
случайных величин – соответствие
между всеми значениями дискретных
случайных величин и их вероятностями.
Обычно его записывают в виде таблицы:
 - сходится.
- сходится. с вероятностями
с вероятностями
 ,
тогда
,
тогда
 .
Если дискретная случайная величина
X
принимает счетное множество возможных
значений, то
.
Если дискретная случайная величина
X
принимает счетное множество возможных
значений, то
 ,
причем М(Х)
существует, если ряд сходится абсолютно.
М(Х)
– неслучайная (постоянная) величина.
Свойства
М(Х)
,
причем М(Х)
существует, если ряд сходится абсолютно.
М(Х)
– неслучайная (постоянная) величина.
Свойства
М(Х) .
. ,
,
 .
Определим произведение постоянной
С на Х как дискретную случайную величин
.
Определим произведение постоянной
С на Х как дискретную случайную величин
 ,
возможные значения которой равны
произведениям С на возможные значения
Х. Вероятность
,
возможные значения которой равны
произведениям С на возможные значения
Х. Вероятность
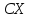 равна вероятностям Х. Например, если
равна вероятностям Х. Например, если
 имеет вероятность
имеет вероятность
 ,
то
,
то
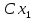 имеет также вероятность
имеет также вероятность
 .
. . М(Х) – константу можно выносить за
знак математического ожидания. Пусть
случайная дискретная величина X задана
законом распределения:
. М(Х) – константу можно выносить за
знак математического ожидания. Пусть
случайная дискретная величина X задана
законом распределения:

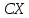 имеет закон распределения:
имеет закон распределения:








 – случайная величина XY,
возможные значения которой равны
произведениям каждого возможного
значения Х на каждое возможное значение
Y.
Вероятности XY
равны произведению соответствующих
вероятностей X
и Y.
– случайная величина XY,
возможные значения которой равны
произведениям каждого возможного
значения Х на каждое возможное значение
Y.
Вероятности XY
равны произведению соответствующих
вероятностей X
и Y. ,
где X,
Y
– независимые дискретные случайные
величины. Пусть законы распределения
вероятностей этих величин:
,
где X,
Y
– независимые дискретные случайные
величины. Пусть законы распределения
вероятностей этих величин:


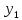
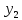




 Закон распределения:
Закон распределения:

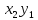


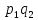

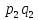
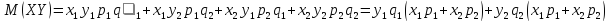
 Возможные значения случайной величины
X
+ Y
равна сумме возможных значений X
и Y
, а вероятность X+Y
равна произведению вероятностей
слагаемых.
Возможные значения случайной величины
X
+ Y
равна сумме возможных значений X
и Y
, а вероятность X+Y
равна произведению вероятностей
слагаемых. .
.

 Х
имеет возможные значения, близкие к
математическому ожиданию, а Y – далекие
от М(Y), таким образом, М(Х) полностью
не характеризует Х. Надо охарактеризовать
отклонение случайной величины от
M(X): отклонение – это величина X – M(X).
Х
имеет возможные значения, близкие к
математическому ожиданию, а Y – далекие
от М(Y), таким образом, М(Х) полностью
не характеризует Х. Надо охарактеризовать
отклонение случайной величины от
M(X): отклонение – это величина X – M(X). ,поэтому
для оценки отклонения берут квадрат
отклонения.
,поэтому
для оценки отклонения берут квадрат
отклонения. .
.

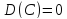
 .
. .
Если
.
Если
 ,
то величина СХ
имеет большие (по модулю) значения,
поэтому
,
то величина СХ
имеет большие (по модулю) значения,
поэтому

 .
Докажем:
.
Докажем:
 Следствие:
Следствие:
 .
. .
Докажем:
.
Докажем:
 .
. ,
равна
,
равна
 ,
где
,
где
 .
Иначе. Дисперсия биноминального
распределения равна
.
Иначе. Дисперсия биноминального
распределения равна

 обозначим через
обозначим через
 .
Если x
изменяется, то изменяется и
.
Если x
изменяется, то изменяется и
 ,
т.е.
,
т.е.
 – функция х.
Функцией
распределения
называют функцию
– функция х.
Функцией
распределения
называют функцию
 ,
определяющую вероятность того, что
случайная величина Х
в результате испытания примет значение,
меньше x,
т.е.
,
определяющую вероятность того, что
случайная величина Х
в результате испытания примет значение,
меньше x,
т.е.
 .
Геометрически
.
Геометрически
 есть вероятность того, что случайная
величина примет значение, которое
изображается точкой левее точки х.
есть вероятность того, что случайная
величина примет значение, которое
изображается точкой левее точки х. ,
т.е.
,
т.е.
 вероятность,
вероятность,
 .
. .
Пусть
.
Пусть
 .
Событие, состоящее в том, что Х
примет значение меньше
.
Событие, состоящее в том, что Х
примет значение меньше ,
можно разделить на 2
несовместных события:
,
можно разделить на 2
несовместных события: ,
с вероятностью
,
с вероятностью

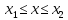 с вероятностью
с вероятностью
 По теореме сложения:
По теореме сложения: отсюда:
отсюда: или
или
 равна приращению
равна приращению
 на этом интервале:
на этом интервале:



 ,
то события
,
то события
 невозможны. Пусть
невозможны. Пусть
 ,
тогда
,
тогда
 – достоверное событие.
– достоверное событие. .
. .
Для описания распределения вероятностей
дискретной случайной величины плотность
распределения неприменима.
.
Для описания распределения вероятностей
дискретной случайной величины плотность
распределения неприменима.
 По формуле Ньютона-Лейбница:
По формуле Ньютона-Лейбница:
 Свойства f(x)
Свойства f(x) ,
т.к.
,
т.к. – неубывающая функция, поэтому,
– неубывающая функция, поэтому,

 Этот интеграл выражает вероятность
события, состоящего в том, что случайная
величина примет значение
Этот интеграл выражает вероятность
события, состоящего в том, что случайная
величина примет значение
 –
достоверное событие, поэтому
–
достоверное событие, поэтому
 .
. ,
тогда:
,
тогда:
 – вероятность того, что случайная
величина примет значение
– вероятность того, что случайная
величина примет значение
 .
. .
Пусть Х
задана плотностью распределения
.
Пусть Х
задана плотностью распределения
 .
Допустим, что все возможные значения
.
Допустим, что все возможные значения
 .
Разобьем его на n
отрезков
.
Разобьем его на n
отрезков
 и
выберем на каждом произвольную точку
и
выберем на каждом произвольную точку
 Тогда
Тогда
 .
Переходя к пределу, получим:
.
Переходя к пределу, получим:
 .
Если возможные значения случайной
величины принадлежат R,
то
.
Если возможные значения случайной
величины принадлежат R,
то
 ,
предполагаем, что этот интеграл
сходится. Дисперсия дискретной
случайной величины:
,
предполагаем, что этот интеграл
сходится. Дисперсия дискретной
случайной величины:
 .
Поступим аналогично:
.
Поступим аналогично:
 .
Если
.
Если
 ,
то
,
то
 .
Более удобная формула:
.
Более удобная формула:
 .
. – среднее квадратическое отклонение
непрерывной случайной величины.
Свойства
– среднее квадратическое отклонение
непрерывной случайной величины.
Свойства
 и
и
 сохраняются
для непрерывных случайных величин.
сохраняются
для непрерывных случайных величин. .
Нормальное распределения определяются
параметрами а
и .
Покажем, что
.
Нормальное распределения определяются
параметрами а
и .
Покажем, что
 .
. .
Введем:
.
Введем:

 .
Первое
слагаемое равно нулю, т.к. функция
нечетная, пределы интегрирования
симметричны относительно начала
координат,
.
Первое
слагаемое равно нулю, т.к. функция
нечетная, пределы интегрирования
симметричны относительно начала
координат,
 (это – интеграл Пуассона). Таким
образом,
(это – интеграл Пуассона). Таким
образом,
 .
. .
Пусть
.
Пусть
 тогда
тогда
 .
.
 ,
тогда
,
тогда


 .
Пусть
.
Пусть
 .
.
 .
. Если
Если

 то
то








 –
объем
выборки.
–
объем
выборки. – сумму частот вариант, попавших в
i-й интервал.
– сумму частот вариант, попавших в
i-й интервал. ,
где
,
где
 – относительная частота.
– относительная частота.
 .
Качество
точечной оценки определяется
характеристиками:
.
Качество
точечной оценки определяется
характеристиками: ,
т.е. совпадает с истинным значением.
,
т.е. совпадает с истинным значением.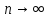 стремится по вероятности к оцениваемому
параметру.
стремится по вероятности к оцениваемому
параметру. .
.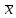 приближается к
приближается к
 ,
является несмещенной, состоятельной
и эффективной.
,
является несмещенной, состоятельной
и эффективной. .
.
 является состоятельной, но смещенной,
поэтому часто используют несмещенную
оценку – исправленную выборочную
дисперсию:
является состоятельной, но смещенной,
поэтому часто используют несмещенную
оценку – исправленную выборочную
дисперсию:

 .
Центральный момент k-го
порядка:
.
Центральный момент k-го
порядка:

 ,
т.е.
,
т.е.
 ,
где *
– найденная характеристика параметра
.
Надежность
,
где *
– найденная характеристика параметра
.
Надежность
 обычно выбирается 0,95; 0,99; 0,999 и т.д.
обычно выбирается 0,95; 0,99; 0,999 и т.д.
 .
Будем рассматривать выборочную среднюю
.
Будем рассматривать выборочную среднюю
 ,
как случайную величину
,
как случайную величину
 ,
для которой
,
для которой

 – случайная величина, т.к.
– случайная величина, т.к. меняется от выборки к выборке).
меняется от выборки к выборке). ,
где
,
где
 ,
– точность оценки. Число t
определяем по таблице значений функции
Лапласа:
,
– точность оценки. Число t
определяем по таблице значений функции
Лапласа:
 .
Получаем:
.
Получаем:
 ,
,
 – интервальная
оценка для математического ожидания
– интервальная
оценка для математического ожидания

 .
Для построения интервальной оценки
используется статистика
.
Для построения интервальной оценки
используется статистика
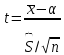 ,
имеющая распределение Стьюдента с
числом степеней свободы
,
имеющая распределение Стьюдента с
числом степеней свободы
 .
Получаем:
.
Получаем:
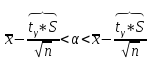 где n
– объем выборки,
где n
– объем выборки,
 –
исправленное среднее квадратическое
отклонение,
–
исправленное среднее квадратическое
отклонение,
 –
выборочная средняя,
–
выборочная средняя,
 – уровень значимости,
– уровень значимости,
 находим по распределению Стьюдента
(t
– распределение) (для двухсторонней
критической области). Точность оценки:
находим по распределению Стьюдента
(t
– распределение) (для двухсторонней
критической области). Точность оценки:
 .
Можно по таблице приложения 3 Гмурмана.
.
Можно по таблице приложения 3 Гмурмана. ,
взята выборка объема n
и вычислена исправленная выборочная
дисперсия
,
взята выборка объема n
и вычислена исправленная выборочная
дисперсия
 .
Требуется определить с надежностью
интервальные оценки для
.
Требуется определить с надежностью
интервальные оценки для

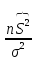 имеет распределение Пирсона
имеет распределение Пирсона степенями свободы. Имеем:
степенями свободы. Имеем:
 .
По таблице
.
По таблице
 - распределения нужно выбрать такие
- распределения нужно выбрать такие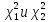 ,
чтобы площадь, заключенная под графиком
плотности распределения
,
чтобы площадь, заключенная под графиком
плотности распределения
 между
между
 ,
была равна
,
была равна
 .
Обычно:
.
Обычно:
 .
. .
Поскольку таблица содержит лишь
.
Поскольку таблица содержит лишь
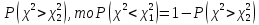 ,
то тогда из
,
то тогда из


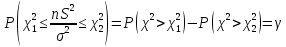 ,
т.е.
,
т.е.
 .
Эта формула используется при решении
обратной задачи – нахождение
доверительной вероятности по заданному
доверительному интервалу генеральной
дисперсии.
.
Эта формула используется при решении
обратной задачи – нахождение
доверительной вероятности по заданному
доверительному интервалу генеральной
дисперсии.
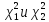 находим
из равенств:
находим
из равенств:
 Запишем неравенство из
Запишем неравенство из
 :
: и
преобразуем его:
и
преобразуем его:
 .
. ,
то доверительный интервал для
,
то доверительный интервал для
 :
:
 .
Если
.
Если
 ,
то
,
то
 ,
где
,
где
 определяется по таблице функции
Лапласа:
определяется по таблице функции
Лапласа:
