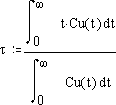Проверка адекватности модели.

 

Любая модель дает приближенное описание процесса функционирования объекта или системы. Поэтому необходима специальная процедура доказательства достоверности (адекватности) построенной модели. От решения задачи оценки адекватности зависит степень доверия к результатам, полученным методом моделирования.

Именно сложность доказательства адекватности предлагаемой модели принято считать важнейшим недостатком метода моделирования.

Фактически единственным, достоверным способом оценки в данном случае является проверка согласованности модели с накопленными знаниями о реальном объекте .

В частности, об адекватности модели можно судить по результатам полученных с ее помощью прогнозных данных.

Кроме того, при оценке адекватности проверяют:

1)     полноту отражения моделью свойств реального объекта;

2)     соответствие модели исходной информации;

3)      корректность принятых при моделировании допущений и ограничений; правильность используемых логических и математических соотношений (функций);

При необходимости в модель вносятся соответствующие коррективы.

Для того ,чтобы можно  было судить  об адекватности модели по результатам прогноза, при одних и тех же условиях замеряются некоторые экспериментальные данные Y_{iэ ,}(где i=1,2,...,n) , и при тех же условиях решаются уравнения  математической модели процесса и получают соответствующие значения  Y_im..По их расхождению и судят об адекватности модели в смысле прогнозирования. Например, для регрессионных моделей используют критерий Фишера .

На рис. представлена общая блок-схема построения математической модели процесса.

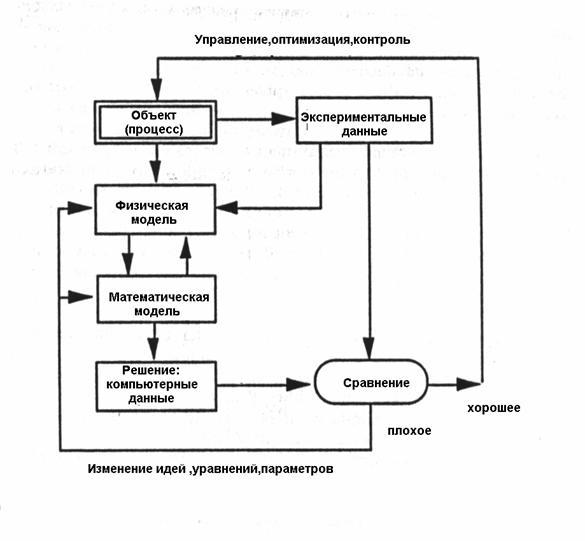
Рис.   Общая блок-схема построения математической модели процесса.

 

 

Любой процесс может быть записан в виде общего уравнения

массоэнергопереноса:

;

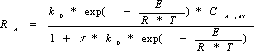где  - потенциал переноса,  а V - конвективная   составляющая ,

 G  - компенсирующая составляющая,    -дополнительные источники или стоки потенциала переноса.

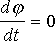      - статический процесс ,              - динамический процесс.

Для однозначного решения этого уравнения необходимо задать 2 типа условий:

1.   Начальные условия  (временные краевые условия).

2.   Граничные условия (пространственные краевые условия).

Граничные условия задают потенциал переноса на всей ограничивающей поверхности, включая границы во все моменты времени, включая начальные.

Начальные условия задают распределение потенциала переноса во всей рассматриваемой области, включая границу в начальный момент времени.

 

Построение математических моделей элементов ХТС.

 

Построение модели начинается с выбора модели для гидродинамики. Можно предложить разные подходы к изучению структуры по­тока и влияния этой структуры на ход химических процессов. Наиболее полную информацию о структуре потока можно по­лучить, зная скорость жидкости в любой точке аппарата, т. е. по­лучив поле скоростей. Но при таком подходе встречаются труднопреодолимые препятствия. Прежде всего, чрезвычайно трудна экспериментальная задача измерения скоростей во всех частях потока. В любом аппарате имеются области, где  почти невозможно измерить скорость, не нарушив структуру потока. Знание поля скоростей лишь в принципе дает возможность решения практических задач. Чаще всего это решение оказывается настолько сложным, что львиной долей информации, которая заключена в данных о поле скоростей, воспользоваться не удается.

Поле скоростей — сложная трехмерная структура, описание которой долж­но содержать функции ,по меньшей мере трех координат.  Не стационарность (например, в турбулентном потоке) добавляет четвертую — время. Математическое описание поля скоростей  получается в виде систем дифферен­циальных уравнений в частных производных; решить такую систему даже с по­мощью современных ЭВМ удается лишь в простейших случаях.

Второй возможный подход —описание потока на основе распределения вре­мени пребывания.

Разработаны две модели идеальных потоков: идеальное вытеснение и идеаль­ное смешение.  Здесь отметим од­ну особенность этих моделей: они не содержат никаких парамет­ров, отражающих специфику структуры потока. Единственный па­раметр этих моделей—среднее время пребывания.

Для определения гидродинамической обстановки в аппарате во входящий поток  добавляют пор­цию какой-либо примеси, называемой   индикато­ром, или трассером. Ин­дикатор должен быть легко количественно определим. Кроме того, его добавление не должно влиять на характер потока (в частности, его следует вводить ма­ло, чтобы существенно не изменять расход), а сам он должен двигаться вместе с потоком, ни с чем не реагируя и не сорбируясь. Так, к потоку воды можно добавить немного кислоты или краси­теля, к воздуху—немного СО2 или  гелия.

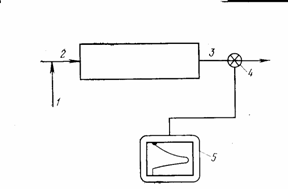
На выходе из аппарата измеряют кон­центрацию индикатора Си как функцию t. Схема установки изобра­жена на рис. . Типичный график зависимости Си от t показан на рис.  В момент t=0 на входе ,например, резким импульсом вводится индикатор (рис. 13,3,а).На выходе (рис. 13.3,6) вначале Си=0: ни одна частица индикатора не успела дойти до выхода. В момент t1 выхо­да достигает самая быстрая часть потока, появляется индикатор. Далее его концентрация нарастает до момента  t2, а затем начи­нает убывать: основная масса потока прошла, выходят те части индикатора, которые попали в зоны циркуляции или застоя.

 

 

Рис. . Схема установки для измере­ния распределения времени пребывания:

1— ввод индикатора; 2 — вход в аппа­рат; 3 — выход из аппарата; 4 — датчик концентрации индикатора; 5 — самопи­шущий прибор.

Результаты эксперимента позволяют определить величину τ:

Время пребывания определяется по формуле: 

 

 

 

 

       

 

 

             

                   t

 

 

       

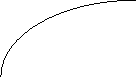
Режим идеального смешения.

                                                    

                                                             

                                                                           t  

 

     

                                                    

 

                                                            Режим идеального вытеснения.                        

      

                                                                

 

                                                                             t

                                               

По экспериментальным данным можно решить одну их двух задач:

        либо по известному объёму реактора V рассчитать расход жидкости W ,

        либо по известному объёмному расходу  W - неизвестный объём.

 

Математическое описания

химического  реактора с мешалкой непрерывного действия

на основе модели идеального  смешения.

 

Химический реактор является одним из наиболее важных элементов химико-технологической схемы .

Модель химического  реактора с мешалкой непрерывного действия  базируется на допущении об идеальном перемешивании реагирующей смеси в зоне реакции, т.е. температура и концентрации компонентов одинаковы во всех точках реактора и на выходе из реактора.

 

 

 

 

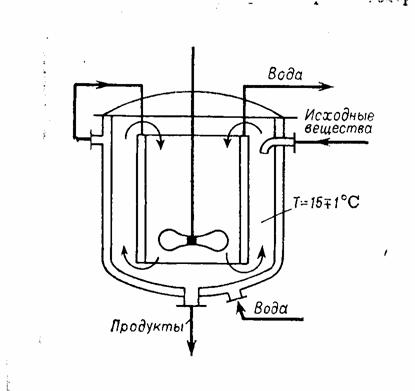
Основным  назначением математического описания такого реактора   является определение из уравнения материального баланса и теплового баланса концентрации и температуры в выходном потоке.

          С точки зрения управления очень важно поддерживать заданное мольное соотношение реагентов на входе в реактор.

          Регулирование температуры осуществляется за счёт подачи хладагента в  охлаждающую рубашку реактора  и в змеевик.

          При превышении температуры выше допустимой , происходит прекращение подачи исходного вещества.

          Введем следующие обозначения:

- объём реактора;  .   -  объемный расход реагирующей смеси.

  -  концентрация  j-го вещества в реакторе и на выходе из него..

          Уравнения материального баланса для вещества  j можно записать  следующим образом:    ,

где   -накопление вещества в реакторе,

      - конвективный приток и сток вещества.

          -количество вещества образующегося в реакторе.

Если накопление вещества в реакторе , то это статический процесс, в случае    - это  динамический процесс.

Уравнение материального баланса можно записать в следующем виде:

,где среднее расчётное время пребывание жидкости в аппарате рассчитывается по  формуле:           

Концентрации веществ  измеряются в кмоль/м³.

Уравнение теплового баланса для реактора имеет вид:

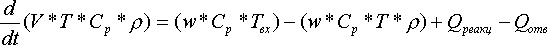
Здесь:

          -накопление тепловой энергии в реакторе,

      - количество теплоты, входящей в реактор,

          - количество теплоты, выходящей из реактора ,

    - количество теплоты ,которое образуется в ходе реакции,

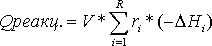
      - теплота, которая отводится из реактора с помощью хладагента.

Уравнение теплового баланса запишем в следующем виде:

,где

 

 

Построение математического описания кинетики химической реакции..

 

Рассмотрим процесс, состоящий из двух стадий химических реакций:

 Каждя стадия характеризуется константой скорости химической реакции .

  

Вводится понятие скорость протекания стадий r₁ и r₂ и скорость протекания реакции по веществам R_A, R_B, R_C, R_D. Для каждой стадии r₁ и r₂применим закон действующих масс, который гласит, что скорость стадий, пропорциональна концентрации исходных веществ в степенях, равных стехиометрическим коэффициентам.

            

Тогда , скорости химических реакций по веществу, будут иметь следующий вид:

    ;       ;       ;