алгем теория

1. Решение СЛАУ. Определители второго прядка.

Решить однородную систему линейных уравнений

Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали:

2. Определители третьего порядка. Формулы Крамера.

Определителем третьего порядка называется следующее выражение:

Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а

зеленым (справа) - со знаком минус.

Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

где - определитель матрицы системы, - определитель матрицы системы, где вместо -го столбца стоит столбец правых частей.

Замечание

Если определитель системы равен нулю, то система может быть как совместной, так и несовместной.

Замечание

1

Данный метод удобно применять для маленьких систем с громоздкими вычислениями, а так же если нужно найти одну из неизвестных. Трудность заключается в том, что необходимо считать много определителей.

Задание. Найти решение СЛАУ 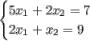при помощи метода Крамера.

Решение. Вычисляем определитель матрицы системы:

Так как , то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель получим из определителя заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:

Аналогично, определитель получается из определителя матрицы системы заменой второго столбца столбцом свободных коэффициентов:

Тогда получаем, что

Ответ. ,

3. Свойства определителей.

Свойство 1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).

Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю. Свойство 3. От перестановки двух строк определитель меняет свой знак.

Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.

Свойство 5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.

Свойство 7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: aij=bj+cj, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.

Свойство 8. Если одна из строк определителя есть линейная комбинация его других строк, то определитеь равен нулю..

Свойство 9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения.

2

4.Матрицы. Основные виды матриц.

Матрицей размера 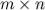называется прямоугольная таблица специального вида, состоящая из строк и столбцов, заполненная некоторыми элементами.

Количество строк и столбцов матрицы задают ее размеры.

Обозначение:

Элементы матрицы обозначаются , где - номер строки, в которой находится элемент, а - номер столбца.

Виды матриц:

Матрица размера 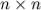называется квадратной, число 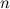называется порядком матрицы.

Пример

- квадратная матрица порядка 2 или матрица второго порядка.

Матрица называется нулевой, если все её элементы равны нулю, т.е. .

Пример

Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, - вектор-столбцом.

Пример - вектор-строка; - вектор-столбец.

Квадратная матрица называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.

Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.

Пример

Скалярной называется диагональная матрица , у которой все диагональные элементы равны между собой.

Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.

Пример

3

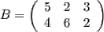
Единичной матрицей называется скалярная матрица порядка , диагональные элементы которой равны 1.

Замечание. Для сокращения записи порядок единичной матрицы можно не писать, тогда единичная матрица обозначается просто .

Пример: - единичная матрица второго порядка.

Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.

Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.

Замечание. Диагональная матрица - это пример матрицы, которая является одновременно верхне- и нижнетреугольной.

Пример - верхнетреугольная матрица.

Ступенчатой называется матрица, удовлетворяющая следующим условиям:

1.если эта матрица содержит нулевую строку (т.е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;

2.если первый ненулевой элемент некоторой строки расположен в столбце с номером , то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем .

5. Действия над матрицами

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Задание. Пусть . Найти матрицу .

Решение.

Ответ.

Суммой матриц и одного размера называется матрица такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Задание. Найти , если ,

4

Решение.

Ответ.

Операции умножение матрицы на число и сумма матриц называются линейными.

Свойства линейных операций:

Везде далее матрицы , и - матрицы одного размера.

1.Ассоциативность

2., где - нулевая матрица соответствующего размера.

3.

4.Коммутативность

5.Дистрибутивность

6.

7.

Произведением матрицы на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы 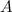на соответствующие элементы -ого столбца матрицы .

Задание. Найти , если

Решение. Так как , а , то в результате получим матрицу размера ,

т.е. матрицу вида . Найдем элементы данной матрицы:

Таким образом, получаем, что:

Все вычисления можно было сделать в более компактном виде:

Ответ.

5

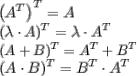
Свойства произведения матриц:

1.Ассоциативность

2.Ассоциативность по умножению

3.Дистрибутивность ,

4.Умножение на единичную матрицу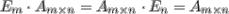

5.В общем случае умножение матриц не коммутативно, т.е.

6.

Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Задание. Найти транспонированную матрицу , если

Решение.

Свойства транспонирования матриц:

6.Обратная матрица.

Матрица называется обратной для матрицы , определитель

которой отличен от нуля , если справедливы равенства , где E – единичная матрица порядка n на n.

Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Алгебраическим дополнением элемента квадратной матрицы

называют минор (n-1)-ого порядка, который получается из матрицы А, вычеркиванием элементов ее i-ой строки и j-ого столбца, умноженный на .

6

Вычислим определитель матрицы А, разложив его по элементам третьего столбца:

Определитель отличен от нуля, так что матрица А обратима.

Найдем матрицу из алгебраических дополнений:

Поэтому

Выполним транспонирование матрицы из алгебраических дополнений:

7

Теперь находим обратную матрицу как :

7.Метод Гауса. Ранг матрицы.

Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых:

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):

8

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

От третьей строки отнимаем вторую, умноженную на 3:

Умножив третью строку на , получаем:

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью:

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

Полученной матрице соответствует система

или

Ответ.

Рангом матрицы называется ранг её системы строк или столбцов.

Обозначается

На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.

Задание. Найти ранг матрицы

9

Решение. С помощью элементарных преобразований над ее строками приведем матрицу к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:

Ко второй строке прибавим пять первых, к третьей - три третьих:

Меняем местами первую и вторую строчки:

Далее четвертую и первую строки:

Ответ.

8. Решение произвольных систем линейных уравнений.

Пусть дана система m линейных уравнений с n неизвестными:

(1)

В матричной форме система (1) имеет вид

АХ = В,