7.4. Теория теплоёмкости Дебая

Дебай рассматривал твердое тело, состоящее из Nодинаковых атомов, как сплошную упругую среду, тепловое движение в которой сводится к акустическим колебаниям всевозможных частот распространяющихся упругих волн. Основную идею Эйнштейна Дебай сохранил, дополнив ее предположением о том, что гармонические осцилляторы колеблются с различными частотами, а их энергия квантована по Планку. Тогда полная тепловая энергия кристалла изNодинаковых атомов выражается формулой:

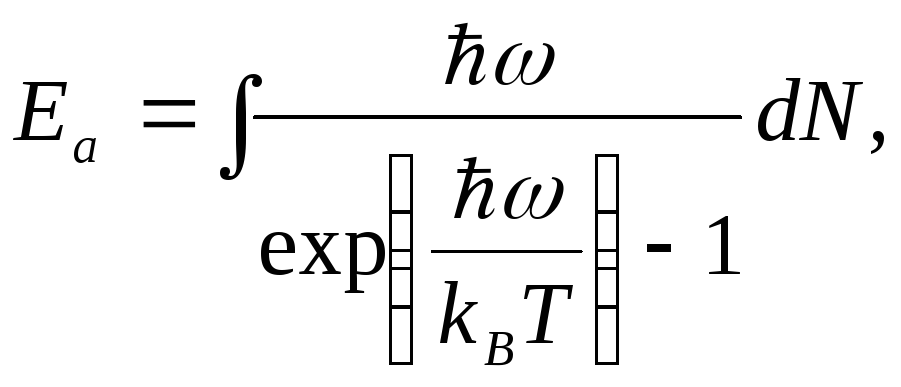(7.2)

где число нормальных колебаний в интервале волновых чисел отk доk+dk. Интегрирование проводится по зоне Бриллюэна. Для определениявыделим вk–пространстве слой толщинойdk, заключенный между сферами радиусов k иk+ dk(рис.7.4). Объем сферического слоя

Разобьем объем этого слоя на ячейки так, чтобы на объем каждой приходилось одно разрешенное значение k. Число допустимых значений волнового числаkв зоне Бриллюэна равно числу элементарных ячеекNв кристалле ( в нашем случае – числу атомов). При этом разрешенные значенияkравномерно распределены вk- пространстве с плотностью , где – объем кристалла. Тогда вk- пространстве на одно разрешенное значениеkприходится ячейка объемом

В сферическом слое объемом число таких ячеек в одной акустической ветви равно

В модели Дебая предполагается, что скорость звука одинакова для всех длин волн и не зависит от направления поляризации, т.е. для всех трех акустических ветвей справедлив линейный закон дисперсии

Тогда , и, следовательно, в интервале междуичисло нормальных колебаний равно

.

Отношение представляет собой плотность мод колебаний решетки одной из поляризаций, т.е. число нормальных мод колебаний, соответствующих единичному интервалу частоты кристалла единичного объема. Функциюназывают спектральной функцией распределения частот.

В твердом теле возможны три типа акустических колебаний – одно продольное со скоростью звука и два поперечных со скоростями звука, поэтому спектральная функция распределения в интервалев силу того, что плотность всех мод равна сумме плотностей отдельных мод, определяется выражением

(7.3)

где ,- усредненная по кристаллографическим направлениям и типам колебаний скорость звука.

С учетом выражения (7.3), формулу для энергии перепишем в виде

. (7.4)

В выражении (7.4) Дебай заменил интегрирование по первой зоне Бриллюэна интегрированием по сфере радиуса , выбираемой таким образом, чтобы эта сфера содержала ровноNразрешенных значений волновых векторов. Это означает, что ее радиусопределяется выражением:

где - объемk- пространства, приходящийся на один разрешенный волновой вектор. Тогда

(7.5)

Если , то, что по порядку величины совпадает с размерами зоны Бриллюэна, а минимальная длина волнысм имеет порядок постоянной кристаллической решеткиа. В решетке не могут распространяться волны с длиной, и максимальная, т.е. дебаевская , частота колебаний, по которой проводится интегрирование в выражении (7.4), в этой модели равна.

При сделанных Дебаем предположениях спектральная функция распределения для всех частот описывается выражением

, (7.6)

что в сумме дает В выражении (7.6)не зависит от частоты и является постоянной.

Н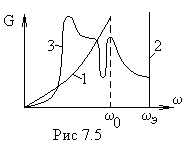а рис.7.5 приведено сравнение спектральных функцийв дебаевском и эйнштейновском приближениях, где кривая 1 – приближение Дебая, кривая 2 – приближение Эйнштейна, кривая 3 истинный спектр колебаний решетки.

Формула (7.4) для любых температур при известной функции распределения (7.6) имеет вид

(7.7)

При вычислении интеграла в выражении (7.7) удобно ввести новые переменные:

(7.8)

Тогда энергия

(7.9)

Подставив (7.5) и (7.8) в формулу (7.9), получаем

(7.10)

Это интерполяционная формула Дебая. В этой формуле энергия, а, следовательно, и теплоемкость при всех температурах выражается через один параметр , называемый характеристической температурой твердого тела или температурой Дебая. Ее физический смысл состоит в том, что величинаесть максимальный квант энергии, способный возбудить колебания решетки. Расчет по формуле (7.8) длядаетК. Температура Дебая зависит от свойств вещества. Для большинства твердых тел она составляет 100- 400К.называется функцией Дебая. Явно вычислить ее нельзя, но аналитические выражения для энергии и теплоемкости модно получит в предельных случаях низких и высоких температур.

В случае высоких температур и. Знаменатель (7.10) разложим в ряд

, тогда выражение (10) принимает вид

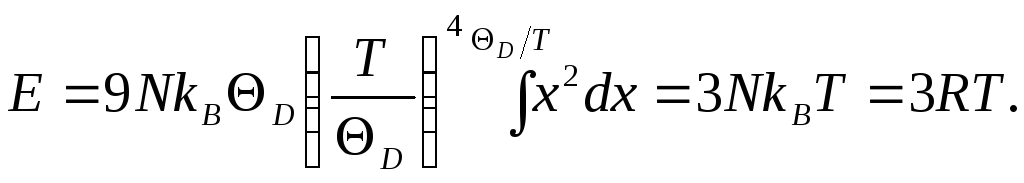
Теплоемкость

не зависит от температуры и изменяется по закону Дюлонга и Пти.

При низких температурах иx>>1. В (7.10) пределы интегрирования от нуля доможно заменить пределами от нуля до бесконечности, тогда, и энергия акустических колебаний

Эта формула является точной при низких температурах, где она правильно описывает зависимость энергии от температуры законом . Теплоемкость при низких температурах описывается кубическим законом:

.

Эта формула хорошо согласуется с экспериментом в узком интервале температур вблизи абсолютного нуля. При более высоких температурах () такого хорошего согласия не наблюдается. Это связано с тем, что при выводе формулы (7.10) для энергии были сделаны достаточно большие упрощения. В частности, задача решалась в гармоническом приближении, когда спектр колебаний можно разделить на независимые моды, что при реальных условиях не может иметь места. Спектральная функция распределениябыла выбрана такой, что существенно отличается от истинной функции распределения (кривые 1 и 3 на рис.7.5), ничем не обоснован резкий обрыв функции на частоте.

В случае решеток с базисом необходимо учитывать вклад в энергию кристалла оптических колебаний решетки. Частота оптических колебаний слабо зависит от волнового вектора, поэтому к ним лучше применима модель Эйнштейна, в которой всем модам приписывается одна частота . В этом приближении каждаяi–тая оптическая ветвь вносит в тепловую энергию вклад

Множитель равен полному числу состояний в каждой ветви спектра,N- число элементарных ячеек,r– число атомов, приходящихся на элементарную ячейку. В общем случае имеется (3r– 3) оптических ветвей, поэтому в удельной теплоемкости, обусловленной акустическими колебаниями, появится дополнительное слагаемое

которое при температуре много большей температуры Эйнштейна, когда возбуждены все моды оптических колебаний, дает постоянный, не зависящий от температуры вклад в теплоемкость. При Т<<вклад оптических колебаний в теплоемкость экспоненциально исчезает и при очень низких температурах, близких к абсолютному нулю, оптические колебания вообще можно не учитывать, так как они не возбуждаются и не дают вклада в тепловую энергию решетки.