1.3. Вынужденные электрические колебания. Резонанс в последовательном контуре

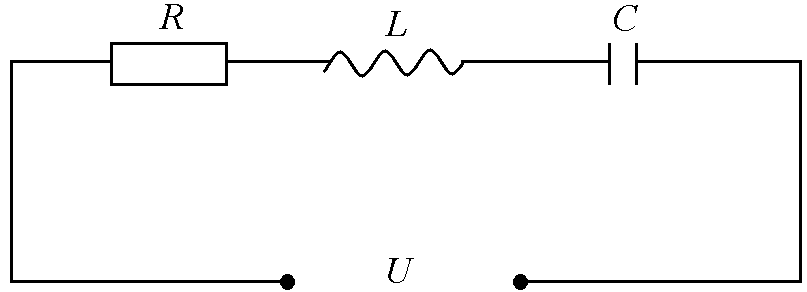
_{Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС или подать на контур переменное напряжение (рис.5).}

Рис. 5

_{Цепь, в которой последовательно с ЭДС включены сопротивление R, индуктивность L и конденсатор С, называется последовательным колебательным контуром. Рассмотрим процессы в этом контуре.}

_{По второму правилу Кирхгофа}

_{или . Разделив на L, получаем уравнение вынужденных колебаний}

₍₂₎

_{Частное решение этого уравнения}

₍₃₎

_{где 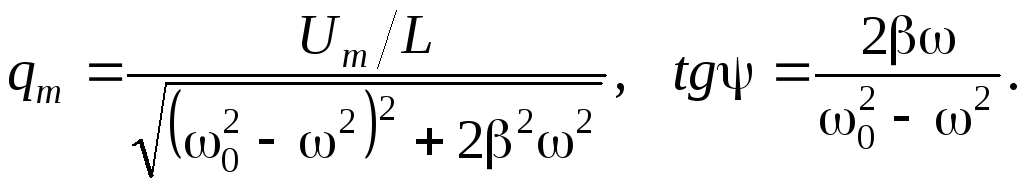Подставим и :}

_{Общее решение получится, если к частному решению (3) прибавить общее решение однородного дифференциального уравнения, которое было получено в предыдущем параграфе. Оно содержит множитель , который очень быстро убывает, и при прошествии достаточно большого времени им можно пренебречь. Таким образом, установившиеся вынужденные электромагнитные колебания в контуре описываются уравнением (3).}

_{Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (3) по времени:}

_{где - сдвиг фаз между током и приложенным напряжением. Тогда}

_{Из этого выражения следует, что ток отстает по фазе от напряжения ()при . И опережает напряжение () при . Для силы тока можно записать}

_{. (4)}

_{Представим соотношение (2) в виде:. Произведение - падение напряжения на активном сопротивлении; - падение напряжения на конденсаторе; – напряжение на индуктивности; тогда можно записать}

_{. (5)}

_{Таким образом, сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.}

_{Согласно (4) - напряжение на активном сопротивлении совпадает по фазе с током в контуре.}

_{Для напряжения на конденсаторе, подставив (3), имеем – напряжение на ёмкости отстаёт от силы тока на π/2.}

_{Напряжение на индуктивности}

_,

_{где , – напряжение на индуктивности опережает ток на π/2.}

_{Фазовые соотношения можно представить наглядно с помощью векторной диаграммы. Действительно, гармонические колебания можно задать с помощью вектора, длина которого равна амплитуде колебаний , а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 6).}

Рис. 6

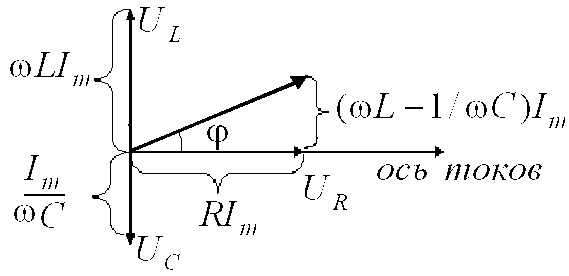
_{совпадает по фазе с током, – отстаёт на π/2), – опережает на π/2. Векторы , , в сумме дают , причём U определяется выражением (5).}

_{При определенной частоте внешнего воздействия в контуре наступает резонанс. Резонансная частота для напряжения на конденсаторе и для заряда q равна:}

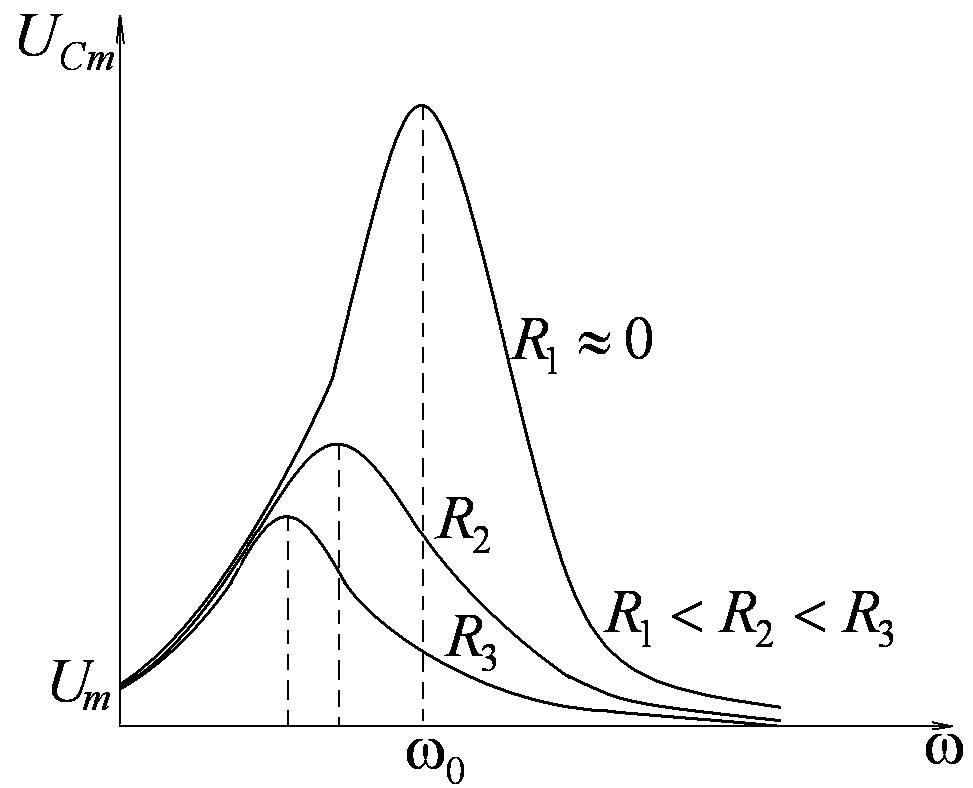
_{Резонансные кривые для имеют вид, представленный на рис.7. Все резонансные частоты . При ω→0 резонансные кривые сходятся в одной точке – это напряжение на конденсаторе при подключении его к источнику постоянного напряжения . Максимум при резонансе тем острее и выше, чем меньше затухание β=R/2L, то есть чем меньше R и больше L. Ход резонансной кривой аналогичен резонансной кривой при механических колебаниях.}

Рис. 7

_{Резонансные кривые для тока приведены на рис. 8.}

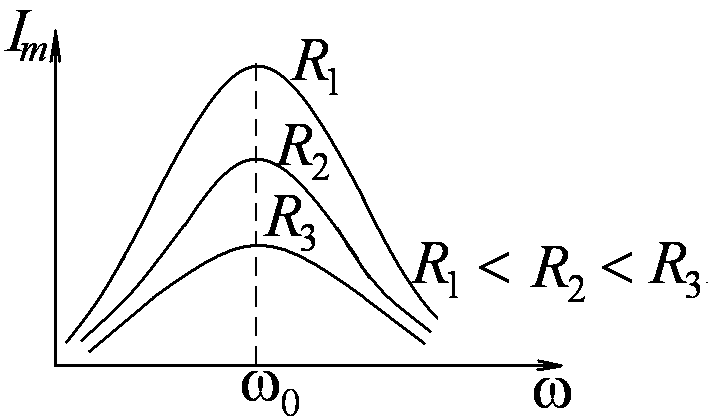
_{Амплитуда силы тока имеет максимальные значения, когда , то есть резонансная частота для силы тока совпадает с собственной частотой колебаний контура:}

Рис. 8

_{При ω→0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.}

_{При малом затухании () резонансную частоту для напряжения можно считать равной . Тогда отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения равно:}

_{– то есть добротность контура показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.}

_{Итак, при резонансе причём поэтому}

– амплитуды напряжений на ёмкости и индуктивности равны между собой, но противоположны по фазе. Поэтому напряжения на ёмкости и индуктивности компенсируют друг друга, и цепь ведёт себя как цепь только с активным сопротивлением. Вся энергия, приложенная к контуру идёт, на Ленц-Джоулево тепло. Ток в цепи достигает максимального значения. Это резонанс напряжений – индуктивного и емкостного.