
- •2.Постоянный электрический ток
- •2.1.Электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока
- •2.2. Электродвижущая сила источника тока
- •2.4. Закон ома для неоднородного участка цепи
- •2.5.Разветвленные цепи. Правила кирхгофа
- •2.6. Мощность тока
- •2.7. Закон джоуля – ленца. Закон видемана-франца
- •3. Магнитостатика
- •3.1. Вектор магнитной индукции
- •3.2.Закон био-савара-лапласа. Магнитное поле движущегося заряда
- •3.3. Магнитное поле прямолинейного проводника с током
- •3.4. Магнитное поле и магнитный дипольный момент кругового тока
- •3.5. Магнитное поле соленоида
- •3.6. Циркуляция магнитного поля. Теорема о циркуляции (закон полного тока). Ротор вектора магнитной индукции
- •3.7. Магнитное взаимодействие постоянных токов. Закон ампера
- •3.8. Сила лоренца. Движение зарядов в электрических и магнитных полях
- •3.9. Работа по перемещению контура с током в магнитном поле
- •3.10. Поток магнитного поля. Дивергенция вектора магнитной индукции
- •3.12. Граничные условия на поверхности раздела двух магнетиков
- •3.13. Классификация магнетиков. Диамагнетики, парамагнетики и ферромагнетики
- •3.14. Эффект холла и его применение
- •4.Электромагнитная индукция
- •4.1. Феноменология электромагнитной индукции. Физика электромагнитной индукции. Правило ленца. Уравнение электромагнитной индукции. Вихревое электрическое поле
- •4.2. Самоиндукция. Индуктивность соленоида
- •4.3. Токи фуко
- •4.4.Ток при замыкании и размыкании цепи
- •4.5.Взаимная индукция
- •4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе
- •4.7. Закон сохранения энергии в неферромагнитной среде
- •5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
- •5.1.Теория максвелла – теория единого электромагнитного поля
- •5.2. Первое уравнение максвелла
- •5.3. Ток смещения. Второе уравнение максвелла
- •5.4.Третье и четвертое уравнение максвелла
- •5.5. Полная система уравнений максвелла электромагнитного поля
- •5.6. Уравнения максвелла– лоренца
3.7. Магнитное взаимодействие постоянных токов. Закон ампера
Ампер
исследовал действие магнитного поля
на проводники с током и показал, что
сила F,
действующая на прямолинейный проводник
с током, находящийся в однородном
магнитном поле, прямо пропорциональна
силе тока I
в проводнике, его длине
![]() ,
магнитной индукции
,
магнитной индукции![]() и синусу угла
и синусу угла![]() между направлениями тока в проводнике
и вектором
между направлениями тока в проводнике
и вектором![]() :
:
![]() .
.
В случае неоднородного магнитного поля и проводника произвольной формы перейдем к бесконечно малым приращениям, имеем:
![]() .
.
![]() -коэффициент
пропорциональности, зависящий от выбора
единицы измерения. В СИ
-коэффициент
пропорциональности, зависящий от выбора
единицы измерения. В СИ
![]() .
.
Будем
считать, что элемент проводника
![]() перпендикулярен вектору
перпендикулярен вектору![]() ,
тогда
,
тогда![]() -магнитная индукция
-магнитная индукция![]() численно равна силе, действующей со
стороны поля на единицу длины проводника,
по которому течет электрический ток
единичной силы и который расположен
перпендикулярно к направлению магнитного
поля. Т.е. магнитная индукция
численно равна силе, действующей со
стороны поля на единицу длины проводника,
по которому течет электрический ток
единичной силы и который расположен
перпендикулярно к направлению магнитного
поля. Т.е. магнитная индукция![]() является силовой характеристикой поля.
является силовой характеристикой поля.
Направление
силы
![]() определяется по правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входили линии магнитной
индукции, а четыре вытянутых пальца
расположить по направлению электрического
тока в проводнике, то отставленный
большой палец укажет направление силы,
действующей на проводник со стороны
поля.
определяется по правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входили линии магнитной
индукции, а четыре вытянутых пальца
расположить по направлению электрического
тока в проводнике, то отставленный
большой палец укажет направление силы,
действующей на проводник со стороны
поля.
Если
![]() не
перпендикулярен
не
перпендикулярен![]() ,
то вектор
,
то вектор![]() совпадает по направлению с векторным
произведением
совпадает по направлению с векторным
произведением![]() -
вектор
-
вектор![]() направлен перпендикулярно к плоскости,
образованной векторами
направлен перпендикулярно к плоскости,
образованной векторами![]() и
и![]() таким образом, чтобы из конца вектора
таким образом, чтобы из конца вектора![]() вращение от вектора
вращение от вектора![]() к вектору
к вектору![]() по кратчайшему пути происходило против
часовой стрелки.
по кратчайшему пути происходило против
часовой стрелки.
Закон Ампера в векторной форме имеет вид:
![]() .
.
Силы электромагнитного взаимодействия не являются центральными и всегда перпендикулярны к линиям магнитной индукции.
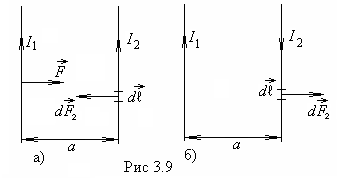 Рассмотрим
два длинных прямолинейных проводника,
которые расположены параллельно друг
к другу. Расстояние между проводниками
а.
При пропускании тока по проводникам
между ними возникает сила взаимодействия.
Рассмотрим некоторые частные случаи.
Рассмотрим
два длинных прямолинейных проводника,
которые расположены параллельно друг
к другу. Расстояние между проводниками
а.
При пропускании тока по проводникам
между ними возникает сила взаимодействия.
Рассмотрим некоторые частные случаи.
1.Пусть
токи
![]() и
и![]() в проводниках направлены в одну сторону
(рис.3.9а). В этом случае проводники
притягиваются друг к другу. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элемент
в проводниках направлены в одну сторону
(рис.3.9а). В этом случае проводники
притягиваются друг к другу. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элемент![]() второго проводника с током
второго проводника с током![]() действует сила
действует сила![]() :
:
![]() .
.
Если
а
<<
![]() ,
то проводник можно считать бесконечно
длинным, тогда
,
то проводник можно считать бесконечно
длинным, тогда
![]() ,
при этом
,
при этом
![]() ,
,![]() ,
имеем
,
имеем![]() .
.
Для
![]() выражение примет такой же вид. Оно
симметрично для обоих проводников,
поэтому
выражение примет такой же вид. Оно
симметрично для обоих проводников,
поэтому
![]() ,
тогда
,
тогда
![]() .
.
2. Если токи противоположны по направлению, то проводники отталкиваются (рис.9б).
Е диницы
измерения в системе СИ: магнитная
индукция -B=[Тл]
– тесла; напряженность магнитного поля
H=[
диницы
измерения в системе СИ: магнитная
индукция -B=[Тл]
– тесла; напряженность магнитного поля
H=[![]() ]
- ампер на метр.
]
- ампер на метр.
Рассмотрим
контур с током, находящийся в магнитном
поле. Сила Ампера, действующая на контур,
равна
![]() ,
интегрирование проводится по контуру
с током. Если поле однородно, вектор
,
интегрирование проводится по контуру
с током. Если поле однородно, вектор![]() можно
вынести за знак интеграла. Интеграл
можно
вынести за знак интеграла. Интеграл![]() представляет собой замкнутую цепочку
элементарных векторов
представляет собой замкнутую цепочку
элементарных векторов![]() ,
поэтому он равен нулю. Поэтому
результирующая амперова сила равна
нулю в однородном магнитном поле. Если
же поле неоднородно, результирующая
сила отлична от нуля . Рассмотрим плоский
контур, размеры которого малы. Такой
контур называют элементарным. Его
магнитный момент
,
поэтому он равен нулю. Поэтому
результирующая амперова сила равна
нулю в однородном магнитном поле. Если
же поле неоднородно, результирующая
сила отлична от нуля . Рассмотрим плоский
контур, размеры которого малы. Такой
контур называют элементарным. Его
магнитный момент![]() ,
где
,
где![]() -
ток в контуре,
-
ток в контуре,![]() -
его площадь,
-
его площадь,![]() - единичный вектор нормали к поверхности
контура, связанный с направлением тока
правилом правого винта. Сила Ампера,
действующая на такой контур в неоднородном
магнитном поле, равна
- единичный вектор нормали к поверхности
контура, связанный с направлением тока
правилом правого винта. Сила Ампера,
действующая на такой контур в неоднородном
магнитном поле, равна![]() ,
где
,
где![]() - производная магнитной индукции на
направление магнитного момента. Из этой
формулы следует:
- производная магнитной индукции на
направление магнитного момента. Из этой
формулы следует:
в
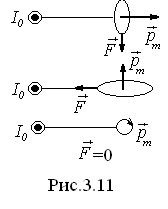 однородном магнитном поле
однородном магнитном поле ,
т.к.
,
т.к.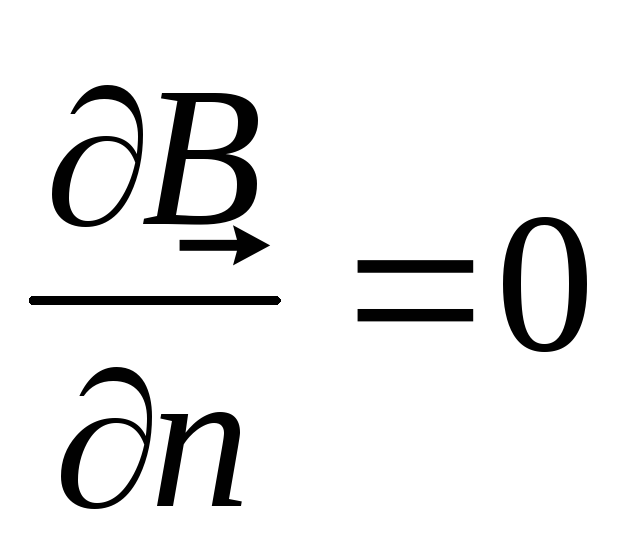 ;
;направление вектора
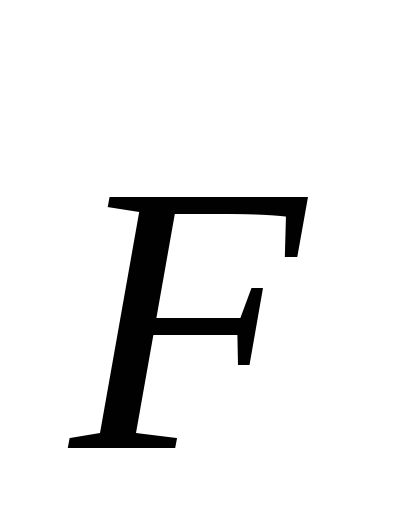 в общем случае не совпадает ни с
вектором
в общем случае не совпадает ни с
вектором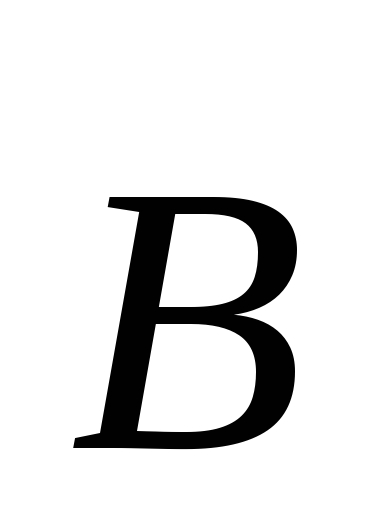 ,
ни с вектором
,
ни с вектором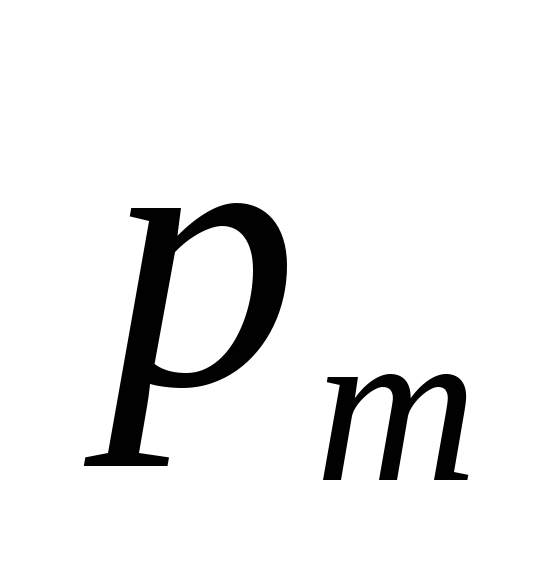 ;
вектор
;
вектор совпадает лишь с направлением
элементарного перемещения
совпадает лишь с направлением
элементарного перемещения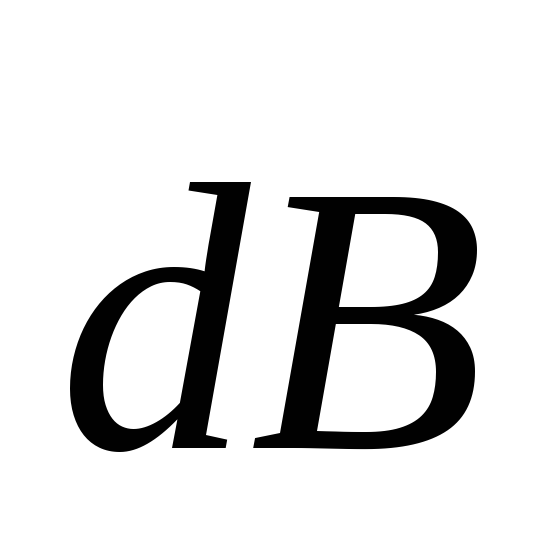 ,
взятого в направлении вектора
,
взятого в направлении вектора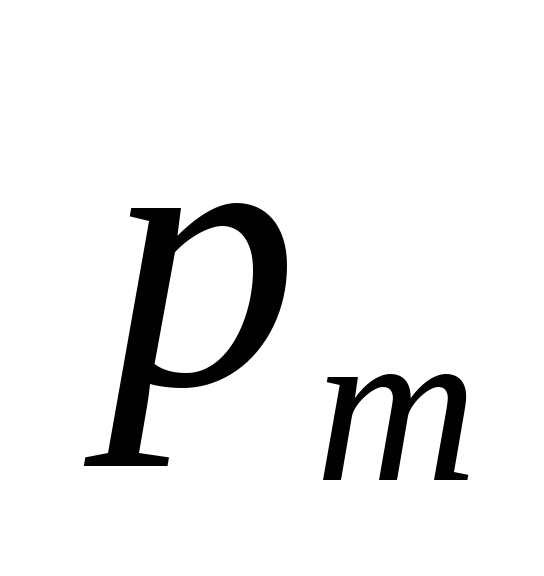 в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ
равна
в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ
равна
![]() .
.
Найдем
момент сил Ампера, действующий на контур
с током в магнитном поле. В однородном
поле результирующая сил, действующих
на контур, равна нулю, следовательно,
суммарный момент этих сил не зависит
от точки О, относительно
которой определяют моменты этих сил. В
этом случае говорят просто о моменте
амперовых сил. Результирующий момент
этих сил
![]() .
Таким образом, результирующий момент
амперовых сил , действующих на контур
с током в однородном магнитном поле,
перпендикулярен магнитному моменту
контура и вектору магнитной индукции.
.
Таким образом, результирующий момент
амперовых сил , действующих на контур
с током в однородном магнитном поле,
перпендикулярен магнитному моменту
контура и вектору магнитной индукции.
