
- •2.Постоянный электрический ток
- •2.1.Электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока
- •2.2. Электродвижущая сила источника тока
- •2.4. Закон ома для неоднородного участка цепи
- •2.5.Разветвленные цепи. Правила кирхгофа
- •2.6. Мощность тока
- •2.7. Закон джоуля – ленца. Закон видемана-франца
- •3. Магнитостатика
- •3.1. Вектор магнитной индукции
- •3.2.Закон био-савара-лапласа. Магнитное поле движущегося заряда
- •3.3. Магнитное поле прямолинейного проводника с током
- •3.4. Магнитное поле и магнитный дипольный момент кругового тока
- •3.5. Магнитное поле соленоида
- •3.6. Циркуляция магнитного поля. Теорема о циркуляции (закон полного тока). Ротор вектора магнитной индукции
- •3.7. Магнитное взаимодействие постоянных токов. Закон ампера
- •3.8. Сила лоренца. Движение зарядов в электрических и магнитных полях
- •3.9. Работа по перемещению контура с током в магнитном поле
- •3.10. Поток магнитного поля. Дивергенция вектора магнитной индукции
- •3.12. Граничные условия на поверхности раздела двух магнетиков
- •3.13. Классификация магнетиков. Диамагнетики, парамагнетики и ферромагнетики
- •3.14. Эффект холла и его применение
- •4.Электромагнитная индукция
- •4.1. Феноменология электромагнитной индукции. Физика электромагнитной индукции. Правило ленца. Уравнение электромагнитной индукции. Вихревое электрическое поле
- •4.2. Самоиндукция. Индуктивность соленоида
- •4.3. Токи фуко
- •4.4.Ток при замыкании и размыкании цепи
- •4.5.Взаимная индукция
- •4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе
- •4.7. Закон сохранения энергии в неферромагнитной среде
- •5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
- •5.1.Теория максвелла – теория единого электромагнитного поля
- •5.2. Первое уравнение максвелла
- •5.3. Ток смещения. Второе уравнение максвелла
- •5.4.Третье и четвертое уравнение максвелла
- •5.5. Полная система уравнений максвелла электромагнитного поля
- •5.6. Уравнения максвелла– лоренца
3.3. Магнитное поле прямолинейного проводника с током
Рассмотрим
прямолинейный проводник
![]() (рис.3.2) , который является частью замкнутой
электрической цепи. По закону
Био-Савара-Лапласа вектор магнитной
индукции
(рис.3.2) , который является частью замкнутой
электрической цепи. По закону
Био-Савара-Лапласа вектор магнитной
индукции![]() поля, создаваемого в точкеА
элементом
поля, создаваемого в точкеА
элементом
![]() проводника с токомI,
имеет значение
проводника с токомI,
имеет значение
![]() ,
где
,
где![]() - угол между векторами
- угол между векторами![]() и
и![]() .
Для всех участков
.
Для всех участков![]() этого проводника векторы
этого проводника векторы![]() и
и![]() лежат в плоскости чертежа, поэтому в
точкеА
все векторы
лежат в плоскости чертежа, поэтому в
точкеА
все векторы
![]() ,
создаваемые каждым участком
,
создаваемые каждым участком![]() ,
направлены перпендикулярно к плоскости
чертежа (к нам). Вектор
,
направлены перпендикулярно к плоскости
чертежа (к нам). Вектор![]() определяется по принципу суперпозиции
полей:
определяется по принципу суперпозиции
полей:
![]() ,
,
его модуль равен:
![]() .
.
Обозначим
расстояние от точки А
до проводника
![]() .
Рассмотрим участок проводника
.
Рассмотрим участок проводника![]() .
Из точкиА
проведем дугу СD
радиуса
.
Из точкиА
проведем дугу СD
радиуса
![]() ,
,![]() – мал, поэтому
– мал, поэтому![]() и
и![]() .
Из чертежа видно, что
.
Из чертежа видно, что![]() ;
;![]() ,
но
,
но![]() (CD=
(CD=![]() )
Поэтому имеем:
)
Поэтому имеем:
![]() .
.
Для
![]() получаем:
получаем:
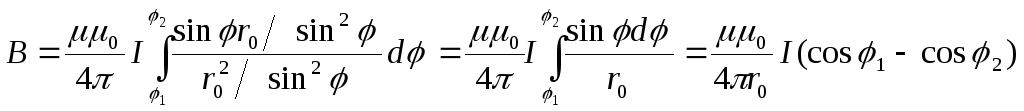 ,
,
где
![]() и
и![]() -
значения угла для крайних точек проводникаMN.
-
значения угла для крайних точек проводникаMN.
Если
проводник бесконечно длинный, то
![]() ,
,![]() .
Тогда
.
Тогда
![]()
индукция в каждой точке магнитного поля бесконечно длинного прямолинейного проводника с током обратно пропорциональна кратчайшему расстоянию от этой точки до проводника.
3.4. Магнитное поле и магнитный дипольный момент кругового тока
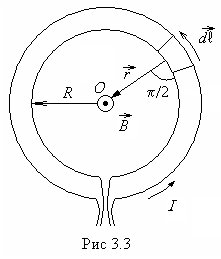 Рассмотрим
круговой виток радиуса R,
по которому течет ток I
(рис. 3.3).
По закону Био- Савара- Лапласа индукция
Рассмотрим
круговой виток радиуса R,
по которому течет ток I
(рис. 3.3).
По закону Био- Савара- Лапласа индукция
![]() поля, создаваемого в точкеО
элементом
поля, создаваемого в точкеО
элементом
![]() витка с током равна:
витка с током равна:
![]() ,
,
причём
![]() ,
поэтому
,
поэтому![]() ,
и
,
и![]() .
С учётом сказанного получаем:
.
С учётом сказанного получаем:
![]() .
.
Все
векторы
![]() направлены перпендикулярно к плоскости
чертежа к нам, поэтому индукция
направлены перпендикулярно к плоскости
чертежа к нам, поэтому индукция
![]() ,
,
напряженность
![]() .
.
Пусть
S
– площадь, охватываемая круговым витком,
![]() .
Тогда магнитная индукция в произвольной
точке оси кругового витка с током:
.
Тогда магнитная индукция в произвольной
точке оси кругового витка с током:
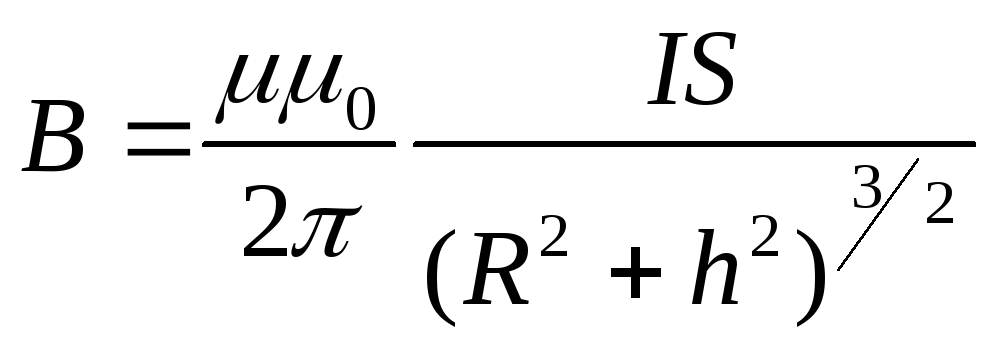 ,
,
где
![]() – расстояние от точки до поверхности
витка. Известно, что
– расстояние от точки до поверхности
витка. Известно, что![]() -
магнитный момент витка. Его направление
совпадает с вектором
-
магнитный момент витка. Его направление
совпадает с вектором![]() в любой точке на оси витка, поэтому
в любой точке на оси витка, поэтому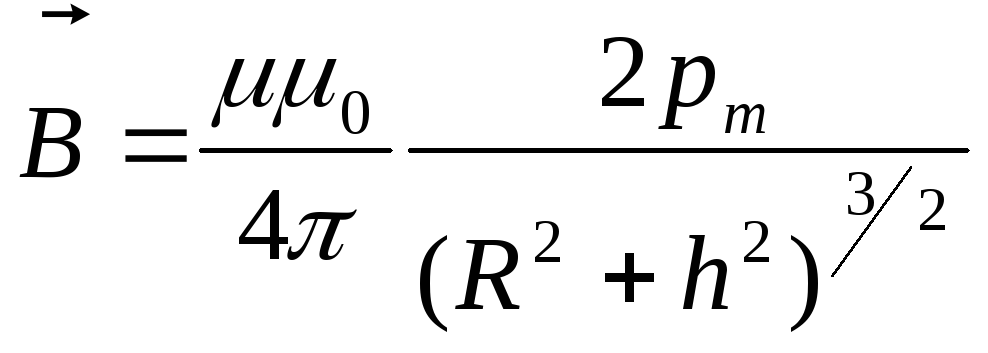 ,
и
,
и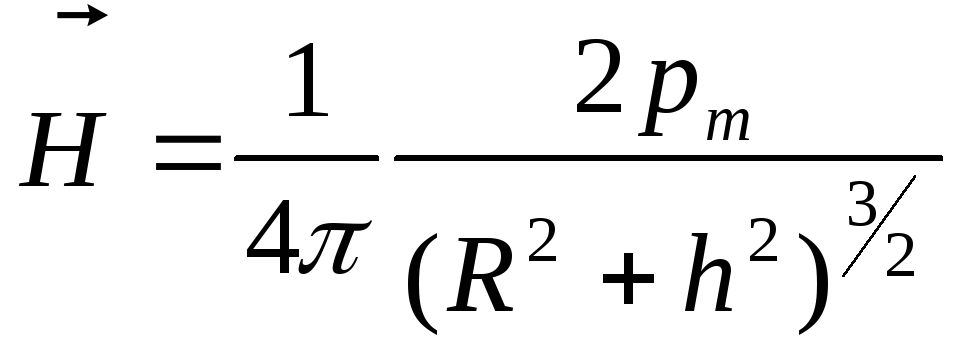 .
.
Выражение
для
![]() по виду аналогично выражению для
электрического смещения в точках поля,
лежащих на оси электрического диполя
достаточно далеко от него:
по виду аналогично выражению для
электрического смещения в точках поля,
лежащих на оси электрического диполя
достаточно далеко от него:
![]() .
.
Поэтому магнитное поле кольцевого тока часто рассматривают как магнитное поле некоторого условного «магнитного диполя», положительным (северным) полюсом считают ту сторону плоскости витка, из которой магнитные силовые линии выходят, а отрицательным (южным) – ту, в которую входят.
Для контура тока, имеющего произвольную форму:
![]() ,
,
где
![]() - единичный вектор внешней нормали к
элементу
- единичный вектор внешней нормали к
элементу![]() поверхностиS,
ограниченной контуром. В случае плоского
контура поверхность S
– плоская и все векторы
поверхностиS,
ограниченной контуром. В случае плоского
контура поверхность S
– плоская и все векторы
![]() совпадают.
совпадают.
3.5. Магнитное поле соленоида
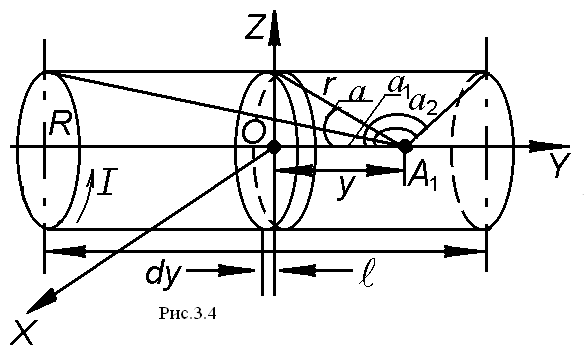
Соленоид - это цилиндрическая катушка с большим числом витков провода. Витки соленоида образуют винтовую линию. Если витки расположены вплотную, то соленоид можно рассматривать как систему последовательно соединенных круговых токов. Эти витки (токи) имеют одинаковый радиус и общую ось (рис.3.4).
Рассмотрим
сечение соленоида вдоль его оси.
Кружками с точкой будем обозначать
токи, идущие из-за плоскости чертежа к
нам, а кружочком с крестиком - токи,
идущие за плоскость чертежа, от нас. L
– длина соленоида, n
– число витков,
приходящихся на единицу длины соленоида;
- R
- радиус витка. Рассмотрим точку А,
лежащую на оси
![]() соленоида. Ясно, что магнитная индукция
соленоида. Ясно, что магнитная индукция![]() в этой точке направлена вдоль оси
в этой точке направлена вдоль оси![]() и равна алгебраической сумме индукций
магнитных полей, создаваемых в этой
точке всеми витками. Проведем из точкиА
радиус – вектор
и равна алгебраической сумме индукций
магнитных полей, создаваемых в этой
точке всеми витками. Проведем из точкиА
радиус – вектор
![]() к какому-либо витку. Этот радиус-вектор
образует с осью
к какому-либо витку. Этот радиус-вектор
образует с осью![]() уголα.
Ток, текущий по этому витку, создает в
точке А
магнитное поле с индукцией
уголα.
Ток, текущий по этому витку, создает в
точке А
магнитное поле с индукцией
![]()
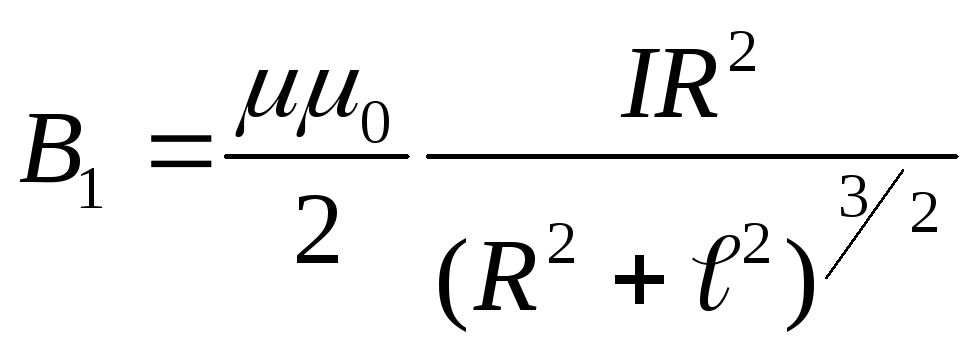 .
.
 Рассмотрим
малый участок
Рассмотрим
малый участок
![]() соленоида, он имеет
соленоида, он имеет![]() витков. Эти витки создают в точкеА
магнитное поле, индукцию которого
витков. Эти витки создают в точкеА
магнитное поле, индукцию которого
![]() .
.
Ясно,
что расстояние по оси от точки А
до участка
![]() равно
равно![]() ;
тогда
;
тогда![]() .Очевидно,
.Очевидно,![]() ,
тогда
,
тогда
![]() ,
,
и
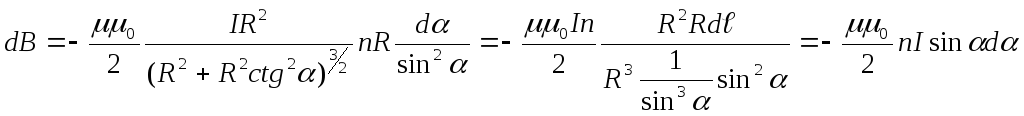 .
.
Магнитная индукция полей, создаваемых всеми витками, в точке А равна
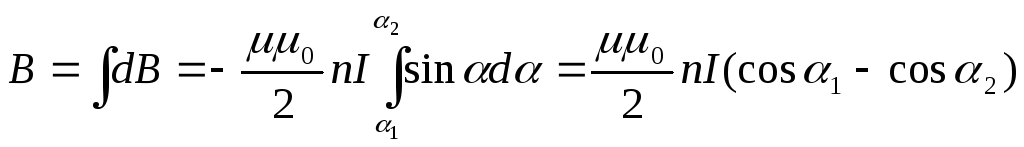 .
.
Напряженность
магнитного поля в точке А
![]() .
.
Из
рис.3. 4 находим:
![]() ;
;![]() .
.
Таким образом, магнитная индукция зависит от положения точки А на оси соленоида. Она
максимальна в середине соленоида:
![]() .
.
Если
L>>
R,
то соленоид можно считать бесконечно
длинным, в этом случае
![]() ,
,![]() ,
,![]() ,
,![]() ;
тогда
;
тогда
![]() ;
;
![]() .
.
На
одном из концов длинного соленоида
![]() ,
,![]() или
или![]() ;
;![]() ,
,![]() ,
,![]() .
.
