3. Магнитостатика

3.1. Вектор магнитной индукции

Подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле, так и в пространстве, окружающем токи, возникает поле, называемое магнитным.

Пространство, в котором на проводник с током или движущийся электрический заряд, а также на тела, обладающие магнитным моментом, действует сила, называется магнитным полем.

Магнитное поле образуется электрическими токами, постоянными магнитами, переменным электрическим полем, и телами, обладающими магнитным моментом. На неподвижный электрический заряд постоянное магнитное поле не действует.

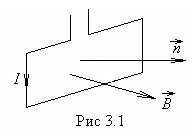
Для изучения свойств магнитного поля пользуются замкнутым плоским контуром с током (рамкой), подвешенным на тонкой нити (рис.3.1). Размеры этого контура должны быть малы по сравнению с расстоянием до тех проводников, по которым текут токи, образующие магнитное поле. Это позволяет считать поле, измеряемое контуром, однородным. Магнитное поле оказывает на рамку с током ориентирующее действие, значит, поле имеет направление.

Проведём нормаль к плоскости рамки. За положительное направление нормали примем такое, чтобы ток в рамке, если смотреть из конца вектора, казался идущим против часовой стрелки. Другими словами, за положительное направление нормали принимают направление поступательного движения буравчика, рукоятка которого вращается в направлении тока, текущего по рамке. Тот факт, что рамка испытывает ориентирующее действие поля (т.е. поворачивается), говорит о том, что на рамку в магнитном поле действует момент пары сил (крутящий момент). Опыт показывает, что величина этого момента максимальна, когда нормаль рамки перпендикулярна к направлению поля. Под действием момента сил рамка поворачивается до тех пор, пока момент сил не станет равным нулю. Это положение устойчивого равновесия. В этом случае нормаль к рамке совпадает с направлением поля.

Магнитное поле характеризуют вектором магнитной индукции . За направлениев данной точке принимают направление положительной нормали к рамке с током в состоянии устойчивого равновесия в этой точке поля. О величине магнитной индукции судят по величине крутящего момента, действующего на рамку при её повороте в магнитном поле:

Далее, из опыта известно, что величина момента пропорциональна току в рамке I и площади рамки S, т.е.

N~ IS.

Вектор, совпадающий по направлению с положительной нормалью к рамке и равный произведению тока в рамке на площадь рамки, называется магнитным моментом рамки:

где _- единичный вектор положительной нормали к рамке.

Следовательно, учитывая вышесказанное, получаем N ~ , где угол между направлением поля и нормалик поверхности рамки (момент силы максимален при/2 и минимален при  

Ясно, что вектор перпендикулярен к плоскости вращения, проходящей через векторыи,тогда. В системе СИ это выражение можно переписать в виде:

Таким образом, располагая пробной рамкой с известным магнитным моментом , можно определять величину и направление магнитного поля (индукции):

Магнитное поле можно представить графически с помощью линий магнитной индукции. Это линии, касательные к которым в каждой точке поля совпадают по направлению с вектором в этой точке поля. Линии магнитной индукции всегда замкнутые, они охватывают проводники с током, а также выходят из северного полюса постоянного магнита и входят в южный.

Для магнитного поля справедлив принцип суперпозиции: поле, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей, порождаемых каждым зарядом в отдельности: