
- •2.Постоянный электрический ток
- •2.1.Электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока
- •2.2. Электродвижущая сила источника тока
- •2.4. Закон ома для неоднородного участка цепи
- •2.5.Разветвленные цепи. Правила кирхгофа
- •2.6. Мощность тока
- •2.7. Закон джоуля – ленца. Закон видемана-франца
- •3. Магнитостатика
- •3.1. Вектор магнитной индукции
- •3.2.Закон био-савара-лапласа. Магнитное поле движущегося заряда
- •3.3. Магнитное поле прямолинейного проводника с током
- •3.4. Магнитное поле и магнитный дипольный момент кругового тока
- •3.5. Магнитное поле соленоида
- •3.6. Циркуляция магнитного поля. Теорема о циркуляции (закон полного тока). Ротор вектора магнитной индукции
- •3.7. Магнитное взаимодействие постоянных токов. Закон ампера
- •3.8. Сила лоренца. Движение зарядов в электрических и магнитных полях
- •3.9. Работа по перемещению контура с током в магнитном поле
- •3.10. Поток магнитного поля. Дивергенция вектора магнитной индукции
- •3.12. Граничные условия на поверхности раздела двух магнетиков
- •3.13. Классификация магнетиков. Диамагнетики, парамагнетики и ферромагнетики
- •3.14. Эффект холла и его применение
- •4.Электромагнитная индукция
- •4.1. Феноменология электромагнитной индукции. Физика электромагнитной индукции. Правило ленца. Уравнение электромагнитной индукции. Вихревое электрическое поле
- •4.2. Самоиндукция. Индуктивность соленоида
- •4.3. Токи фуко
- •4.4.Ток при замыкании и размыкании цепи
- •4.5.Взаимная индукция
- •4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе
- •4.7. Закон сохранения энергии в неферромагнитной среде
- •5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
- •5.1.Теория максвелла – теория единого электромагнитного поля
- •5.2. Первое уравнение максвелла
- •5.3. Ток смещения. Второе уравнение максвелла
- •5.4.Третье и четвертое уравнение максвелла
- •5.5. Полная система уравнений максвелла электромагнитного поля
- •5.6. Уравнения максвелла– лоренца
4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе
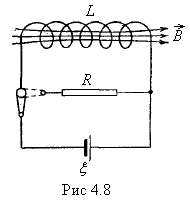 Рассмотрим
цепь, состоящую из соленоида, замкнутого
на источник тока (рис.4.8), находящуюся в
неферромагнитной среде. В соленоиде
течет ток
Рассмотрим
цепь, состоящую из соленоида, замкнутого
на источник тока (рис.4.8), находящуюся в
неферромагнитной среде. В соленоиде
течет ток
![]() ,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление
,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление![]() ,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
время
,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
время![]() равна
равна
![]() .
.
Если
индуктивность соленоида остается
постоянной,
![]() ,
то
,
то![]() ,
и
,
и
![]() .
(4.3)
.
(4.3)
Эта работа идет на нагревание проводников. Вследствие совершения этой работы происходит исчезновение магнитного поля, и так как никаких изменений в окружающей цепь среде не происходит, следует заключить, что работа совершается за счет энергии магнитного поля, а выражения (4.3) как раз и определяет эту работу. Вся работа, произведенная током при убывании магнитного поля до нуля равна
![]() ,
,
и
энергия магнитного поля
![]() .
.
Объемной
плотностью энергии
![]() магнитного поля называется энергия
этого поля, отнесенная к его объему:
магнитного поля называется энергия
этого поля, отнесенная к его объему:
![]() .
.
Однако
![]() (
поле соленоида однородно), согласно
закону полного тока в случае поля
соленоида получаем
(
поле соленоида однородно), согласно
закону полного тока в случае поля
соленоида получаем![]() ,
где
,
где![]() - длина соленоида,
- длина соленоида,![]() - число витков соленоида, тогда
- число витков соленоида, тогда
![]() .
.
Энергия
![]() ,
локализованная во всем объеме магнитного
поля равна:
,
локализованная во всем объеме магнитного
поля равна:
![]() .
.
Если поле в данной точке пространства создано несколькими контурами с током, то энергия результирующего магнитного поля равна:
![]() ,
,
где
![]() -
сила тока в
-
сила тока в![]() -том
контуре,
-том
контуре,![]() -
потокосцепление
-
потокосцепление![]() -
того контура, равное сумме
потокосцепления самоиндукции (магнитного
потока самоиндукции)
-
того контура, равное сумме
потокосцепления самоиндукции (магнитного
потока самоиндукции)![]() -того
контура и магнитного потока взаимоиндукции
-того
контура и магнитного потока взаимоиндукции
![]() -того
контура с остальными ,
-того
контура с остальными ,![]() .
Поэтому энергия магнитного поля равна
.
Поэтому энергия магнитного поля равна
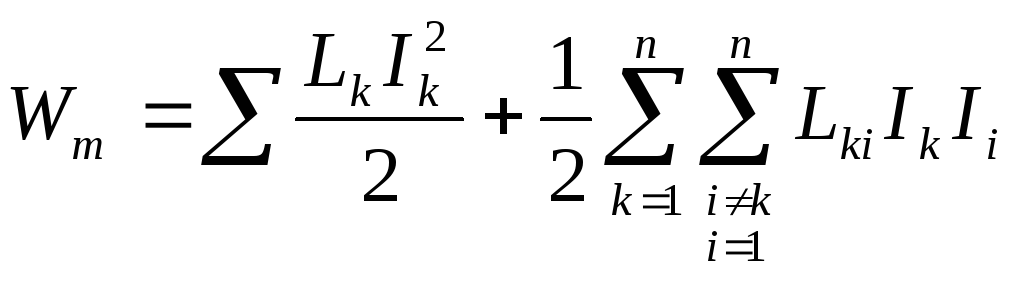 ,
,
![]() –взаимная индуктивность
–взаимная индуктивность
![]() -того
иi-
того контуров с токами
-того
иi-
того контуров с токами
![]() и
и![]() .
.
4.7. Закон сохранения энергии в неферромагнитной среде
Энергия магнитного поля, создаваемого какой-либо системой тел (проводящих контуров с токами) изменяется, если контуры с токами перемещаются, или, если изменяются токи в них.
При этом совершают работу внешние силы, приложенные к телам системы, источники электрической энергии, включенные в цепи токов.
Если температура системы постоянна, и плотность среды не меняется, то закон сохранения энергии можно записать в виде:
![]() ,
,
здесь
![]() - работа внешних сил в рассматриваемом
процессе,
- работа внешних сил в рассматриваемом
процессе,![]() - работа источников электрической
энергии,
- работа источников электрической
энергии,![]() - изменение энергии магнитного поля,
- изменение энергии магнитного поля,![]() - изменение кинетической энергии тел
системы,
- изменение кинетической энергии тел
системы,![]() - теплота Джоуля-Ленца.
- теплота Джоуля-Ленца.
Если
тела системы перемещаются очень медленно
(квазистатически), то можно пренебречь
изменением кинетической энергии
системы,
![]() =0,
и можно считать
=0,
и можно считать![]() ,
где
,
где![]() -
работа сил, действующих на тела системы
в магнитном поле. Это пондемоторные
силы. Тогда закон сохранения энергии
примет вид:
-
работа сил, действующих на тела системы
в магнитном поле. Это пондемоторные
силы. Тогда закон сохранения энергии
примет вид:
![]() .
.
Если система содержит n проводящих контуров с токами, работа источников электрической энергии за малый промежуток времени dt равна:
![]() ,
,
где
![]() – алгебраическая сумма ЭДС всех
источников электрической энергии,
включенных в
– алгебраическая сумма ЭДС всех
источников электрической энергии,
включенных в![]() -тый
контур,
-тый
контур,![]() – сила тока в этом контуре.
– сила тока в этом контуре.
Рассмотрим некоторые примеры.
Неподвижный контур с током.
а) Если
ток в контуре остается постоянным, то
энергия магнитного поля
![]() не изменяется,
не изменяется,![]() ,
а пондемоторные силы не совершают
работы:
,
а пондемоторные силы не совершают
работы:![]() ,
поэтому
,
поэтому![]()
- вся работа источника электрической энергии преобразуется в контуре в тепло Джоуля-Ленца.
б)
Пусть ток в контуре растет от 0 до
![]() .
Работа пондемоторных сил равна нулю и
работа источника электрической энергии
в контуре расходуется на изменение
знергии магнитного поля и на выделение
тепла Джоуля-Ленца:
.
Работа пондемоторных сил равна нулю и
работа источника электрической энергии
в контуре расходуется на изменение
знергии магнитного поля и на выделение
тепла Джоуля-Ленца:![]() ,
или
,
или![]() ,
где
,
где![]() -
ЭДС источника,R
- сопротивление, L
– индуктивность контура, I
-сила тока в нем.
-
ЭДС источника,R
- сопротивление, L
– индуктивность контура, I
-сила тока в нем.
Работа пондемоторных сил при очень медленной деформации контура с током. Закон сохранения энергии имеет вид:
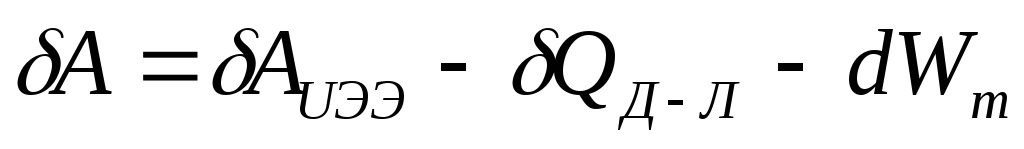 .
Сила токаI
в контуре изменяется под влиянием ЭДС
самоиндукции
.
Сила токаI
в контуре изменяется под влиянием ЭДС
самоиндукции
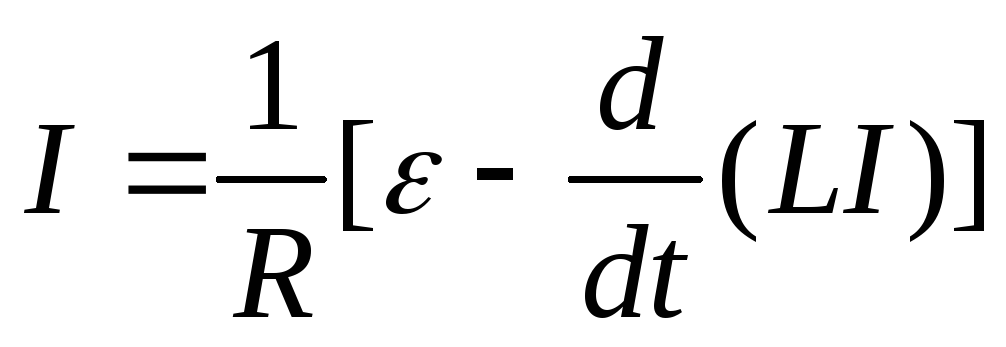 ,
где
,
где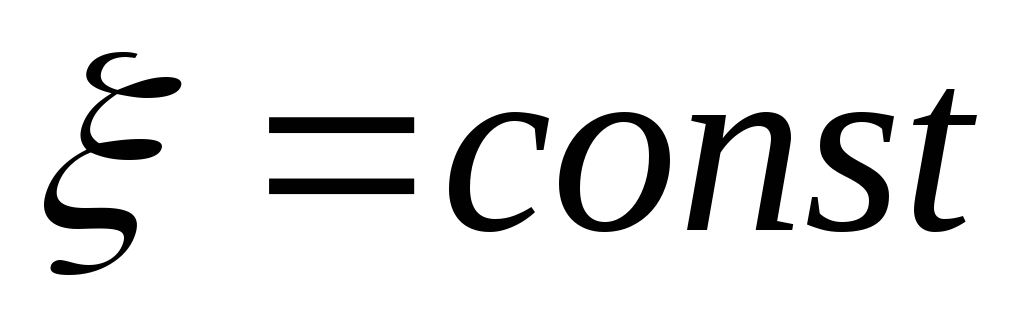 – ЭДС источника постоянного тока в
контуре, тогда работа источников
электрической энергии
– ЭДС источника постоянного тока в
контуре, тогда работа источников
электрической энергии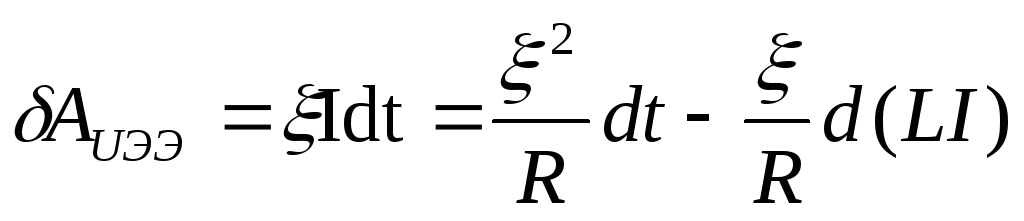
При
очень медленной деформации контура ЭДС
самоиндукции мала по сравнению с
![]() ,
поэтому теплота, выделяемая по закону
Джоуля-_Ленца, равна
,
поэтому теплота, выделяемая по закону
Джоуля-_Ленца, равна![]() ,
и
,
и![]() .
.
Таким
образом, элементарная работа пондемоторных
сил
![]() .
Полная работа пондемоторных сил
.
Полная работа пондемоторных сил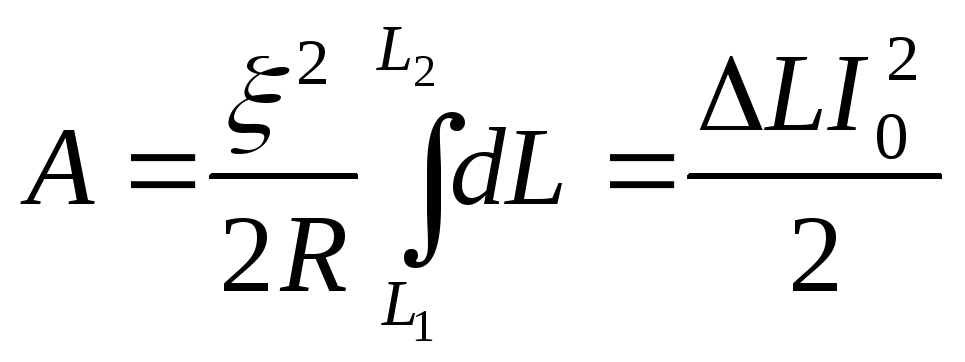 ,
где
,
где![]() – изменение индуктивности контура при
его деформации,
– изменение индуктивности контура при
его деформации,![]() – постоянный ток в контуре до и после
его деформации.
– постоянный ток в контуре до и после
его деформации.
Лекция 9
