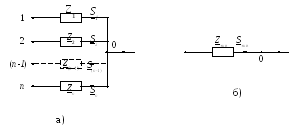- •Оглавление
- •Глава 1. Введение в электроэнергетику. Цели и задачи курса. Основные понятия. Номинальные напряжения
- •Физическая природа электричества
- •Свойства электроэнергии
- •Цель и задачи курса
- •Электрическая сеть, как часть электрической системы
- •Номинальные напряжения
- •Область использования номинальных напряжений
- •Глава 2. Классификация электрических сетей
- •Глава 3. Основные сведения о конструкциях линий электропередач
- •3.1. Воздушные линии электропередас (влэп)
- •3.2. Кабельные линии электропередач (клэп)
- •Глава 4. Схемы замещения и параметры элементов электрических сетей
- •4.1. Активное сопротивление
- •4.2. Индуктивное сопротивление
- •4.3. Активная проводимость
- •4.4. Реактивная (емкостная проводимость)
- •4.5. Схема замещения лэп
- •Глава 5. Параметры схемы замещения трансформаторов
- •5.1. Общие сведения
- •5.2. Двухобмоточный трансформатор
- •5.3 Трехобмоточный трансформатор
- •5.4. Двухобмоточный трансформатор с расщепленной обмоткой низкого напряжения
- •5.5. Автотрансформатор
- •100 % / 100 % / Α %.
- •Глава 6. Характеристики основных электроприемников
- •6.1. Характеристики основных электроприемников
- •6.2. Графики нагрузки электроприемников
- •Глава 7. Потери мощности и электроэнергии в элементах сети
- •7.1. Потери мощности в элементах сети
- •7.2. Расчет потерь мощности в линиях электропередач
- •7.3. Расчет потерь мощности в лэп с равномерно распределенной нагрузкой
- •7.4. Расчет потерь мощности в трансформаторах
- •7.5. Приведенные и расчетные нагрузки потребителей
- •7.6. Расчет потерь электроэнергии
- •Мероприятия по снижению потерь мощности
- •Глава 8. Векторные диаграммы лэп
- •8.1. Векторная диаграмма лэп 35 кВ с одной нагрузкой
- •8.2. Векторная диаграмма лэп 35 кВ с несколькими нагрузками
- •8.3. Векторная диаграмма лэп 110 кВ с одной нагрузкой
- •Глава 9. Расчет режимов электрических сетей
- •9.1. Задача расчета режимов. Основные допущения
- •9.2. Метод расчета режима при заданном напряжении в конце лэп
- •9.3. Последовательность расчета
- •9.4. Расчет режима при заданном напряжении в начале лэп (на источнике питания)
- •9.5. Расчет сетей разных номинальных напряжений
- •Глава 10. Расчет местных сетей (сетей напряжением ) по потере напряжения
- •10.1. Допустимые потери напряжения в линиях местных сетей
- •10.2. Допущения, положенные в основу расчета местных сетей
- •10.3. Определение наибольшей потери напряжения
- •В неразветвленной сети наибольшая потеря напряжения – это потеря напряжения от ип до конечной точки сети. В разветвленной сети наибольшая потеря напряжения определяется следующим образом:
- •10.4. Частные случаи расчета местных сетей
- •Потеря напряжения в лэп с равномерно распределенной нагрузкой
- •Глава 11. Расчет сечений проводов по допустимой потере напряжения
- •11.1. Общие положения методов
- •11.2. Расчет сечений проводов из условия постоянства сечений на участках
- •11.3. Расчет сечений проводов из условия минимального расхода проводникового материала
- •11.4. Расчет сечений проводов из условия минимума потерь мощности в сети
- •11.5. Этапы расчета при разных условиях
- •11.6. Сравнительная характеристика методов
- •Глава 12. Расчет режимов простых замкнутых сетей
- •12.1. Расчет линий с двухстронним питанием
- •12.2. Частные случаи расчета простых замкнутых сетей
- •Глава 13. Расчет режимов сложнозамкнутых сетей. Методы преобразования сети.
- •13.1. Суть метода преобразования
- •13.2. Прием 1. Замена площади сечения проводов участка сети эквивалентной
- •13.3. Прием 2. Замена параллельных линий при отсутствии на них нагрузок эквивалентной линей
- •13.4. Прием 3. Замена источников напряжения, присоединенных к одной точке сети, одним эквивалентным
- •13.5. Прием 4. Преобразование треугольника сопротивлений в эквивалентную звезду
- •13.6. Прием 5. Перенос нагрузок в другие точки сети
- •Глава 14. Баланс мощностей в энергосистеме
- •Глава 15. Реактивная мощность в энергосистеме. Потребители реактивной мощности. Выработка реактивной мощности генераторами эс
- •15.1. Общие положения
- •15.2. Регулирующий эффект нагрузки
- •15.3. Потребители реактивной мощности
- •15.4. Генерация реактивной мощности генераторами эс
- •Глава 16. Реактивная мощность в энергосистеме. Компенсация реактивной мощности.
- •16.1. Общие положения
- •16.2. Синхронные компенсаторы
- •16.3. Батареи конденсаторов
- •16.4 Поперечная компенсация
- •16.5. Продольная компенсация
- •16.6. Статические источники реактивной мощности
- •Глава 17. Методы регулирования напряжения. Устройства регулирования напряжения
- •17.1. Общие положения
- •17.2. Регулирование напряжения в центрах питания
- •17.3. Метод встречного регулирования
- •17.4. Регулирование напряжения на электростанциях
- •17.5. Регулирование напряжения на понижающих подстанциях
- •17.6. Устройство рпн двухобмоточного трансформатора
- •17.7. Устройство рпн автотрансформатора
- •Глава 18. Методы регулирования напряжения. Устройства регулирования напряжения (продолжение)
- •18.1. Выбор ответвлений двухобмоточного трансформатора
- •18.2. Выбор ответвлений трехобмоточного трансформатора и автотрансформатора
- •Глава 19. Методы регулирования напряжения. Устройства регулирования напряжения (продолжение)
- •19.1. Регулирование напряжения при помощи линейных регуляторов
- •19.2. Регулирование напряжения при помощи устройств продольной компенсации
- •19.3. Регулирование напряжения при помощи устройств поперечной компенсации
- •Глава 20. Экономичность режимов электрических систем
- •20.1. Общие сведения
- •20.2. Оптимальное распределение активной мощности между тепловыми электростанциями
- •20.3. Оптимальное распределение мощности в замкнутых сетях
- •20.4. Принудительное перераспределение мощности
- •20.5. Настройка сети
- •20.5. Размыкание пути протекания уравнительного тока, то есть размыкание контуров сети
- •20.6. Экономичный режим работы трансформаторов
13.3. Прием 2. Замена параллельных линий при отсутствии на них нагрузок эквивалентной линей
Прямая
задача.
Известны мощности
![]() параллельных линий и их сопротивления
параллельных линий и их сопротивления![]() (см. рис. 13.1 а). Необходимо найти значения
(см. рис. 13.1 а). Необходимо найти значения![]() и
и![]() в преобразованной схеме (см. рис. 13.1 б).
в преобразованной схеме (см. рис. 13.1 б).
Условие эквивалентности схем – одинаковое напряжение в точке 0 в преобразованной и исходной схемах.
Если напряжение в точках 1 – n одинаково, то мы можем записать:
![]() и
и
![]()
|
|
|
Рисунок 13.1 – Пояснения к приему 2: а) исходная схема; б) преобразованная схема |
Эквивалентная проводимость схемы рассчитывается по формуле:
![]()
![]()
Обратная
задача.
Известны мощность
![]() и сопротивление
и сопротивление![]() в преобразованной схеме (см. рис. 13.1 б).
Найти мощности
в преобразованной схеме (см. рис. 13.1 б).
Найти мощности![]() в исходной схеме (см. рис. 13.1 а).
в исходной схеме (см. рис. 13.1 а).
Так как напряжение в точке 0 одинаково, то одинаково падение напряжения на сопротивлениях в преобразованной и исходной схемах:
![]()
![]()
или
![]()
Из
полученного равенства можно найти
значения можностей
![]() :
:
![]()
![]()
![]() …
…![]()
13.4. Прием 3. Замена источников напряжения, присоединенных к одной точке сети, одним эквивалентным
Прямая
задача.
Известны значения токов
![]() параллельных линий, их сопротивления
параллельных линий, их сопротивления![]() и значения фазных ЭДС
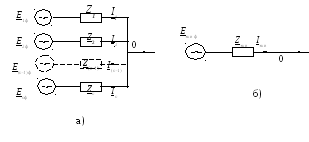
и значения фазных ЭДС![]() (см. рис. 13.2 а). Необходимо найти значения
(см. рис. 13.2 а). Необходимо найти значения![]() и
и![]() в преобразованной схеме (см. рис. 13.2 б).
в преобразованной схеме (см. рис. 13.2 б).
Условие эквивалентности схем – одинаковое напряжение в точке 0 в преобразованной и исходной схемах.
|
|
|
Рисунок 13.2 – Пояснения к приему 3: а) исходная схема; б) преобразованная схема |
Значение токов в ветвях исходной схемы рассчитываются по выражениям:
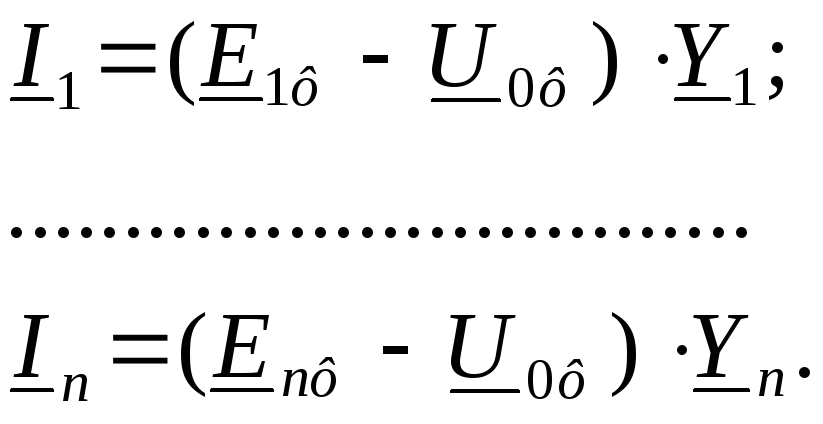 (13.1)
(13.1)
Значение тока в эквивалентной сети равно:
![]() (13.2)
(13.2)
Подставим выражение (13.1) в (13.2):
![]()
Так
как
![]() ,
то полученное выражение можно записать
так:
,
то полученное выражение можно записать
так:
![]() .
.
Раскроем скобки и выполним преобразования. В результате получим следующее выражение:
![]() или
или
![]()
Откуда величина эквивалентной фазной ЭДС будет равна:
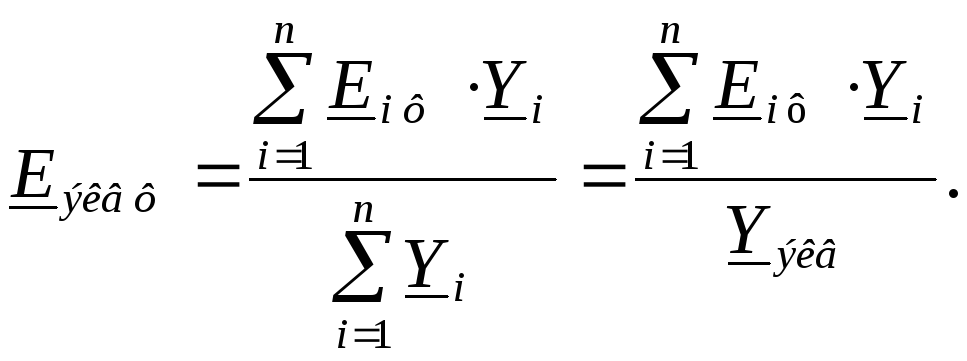
Обратная
задача.
Известны значения
![]() и
и![]() в преобразованной схеме (см. рис. 13.2 б)
Необходимо найти значения токов
в преобразованной схеме (см. рис. 13.2 б)
Необходимо найти значения токов![]() в исходной схеме (см. рис. 13.2 а).
в исходной схеме (см. рис. 13.2 а).
Величина падения напряжения на сопротивлениях в исходной схеме определяется как:
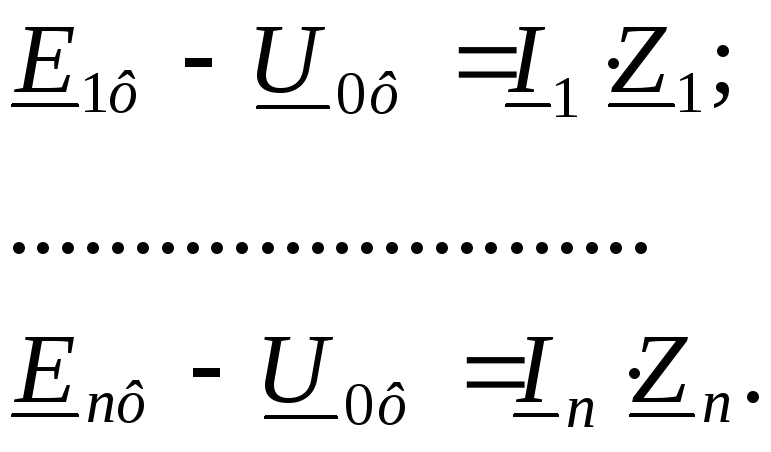
Аналогичное выражение можно записать для преобразованной схемы:
![]()
Из полученных выражений найдем значение напряжения в точке 0:
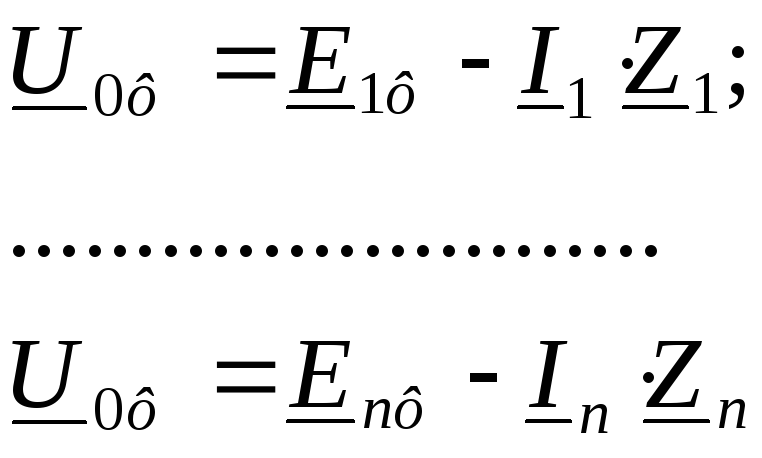 (13.3)
(13.3)
и
![]() (13.4)
(13.4)
Приравняем поочередно выражения из (13.3) к выражению (13.4):
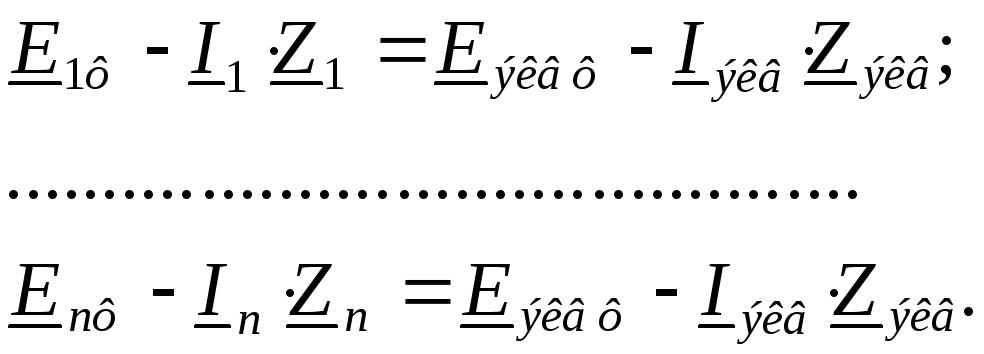
Из этих равенств можно определить искомые значения токов:
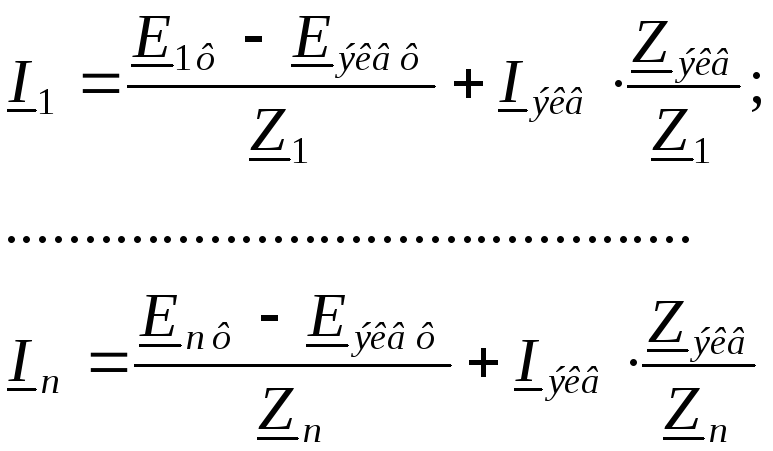
Чтобы
определить значения мощностей в ветвях,
нужно сопряженные комплексы токов
умножить на значение напряжения в точке
0 и на
![]() :
:
![]()
13.5. Прием 4. Преобразование треугольника сопротивлений в эквивалентную звезду
Прямая
задача.
Известны значения мощностей в ветвях
треугольника
![]() ,
их сопротивления
,
их сопротивления![]() .
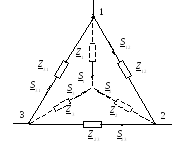
(см. рис. 13.3). Необходимо найти значения
мощностей
.
(см. рис. 13.3). Необходимо найти значения
мощностей![]() в лучах звезды и их сопротивления
в лучах звезды и их сопротивления![]() .
.
|
|
|
Рисунок 13.3 – Пояснения к приему 4 |
Условие эквивалентности схем – режим за точками 1, 2 и 3 остается неизменным до и после преобразования.
Сопротивления лучей звезды рассчитываются по формулам:
![]()
![]()
![]()
Мощности в лучах звезды определяются по I закону Кирхгофа, составленного для узлов 1, 2, 3. При принятых направлениях мощностей получим:
![]()
![]()
![]()
Обратная
задача.
Известны значения мощностей
![]() в лучах звезды и их сопротивления
в лучах звезды и их сопротивления![]() (см. рис. 13.3). Необходимо найти значения
мощностей в ветвях треугольника
(см. рис. 13.3). Необходимо найти значения
мощностей в ветвях треугольника![]() ,
их сопротивления
,
их сопротивления![]() .
.
Сопротивления сторон треугольника рассчитываются по формулам:
![]()
![]()
![]()
Мощности в ветвях треугольника рассчитываются по II закону Кирхгофа, составленного для замкнутых контуров. При принятом направлении обхода контуров по часовой стрелке, имеем следующие уравнения:
![]()
![]()
![]()
Решая полученные уравнения, определяем значения мощностей в треугольнике:
![]()
![]()
![]()
Прямым может быть преобразование звезды в треугольник. Тогда обратная задача – преобразование треугольника в звезду.