
Производные и дифференциалы
10. Частные приращения и частные производные
Пусть функция
![]() определена в некоторой (открытой)
областиD точек
определена в некоторой (открытой)
областиD точек![]() мерного пространства, и
мерного пространства, и![]() – точка в этой области, т.е.
– точка в этой области, т.е.
![]() D.
D.
Частным приращением функции многих переменных по какой-либо переменной называется то приращение, которое получит функция, если мы дадим приращение этой переменной, считая, что все остальные переменные имеют постоянные значения.
Например,
частное приращение функции
![]() по переменной
по переменной![]() будет
будет
![]() .
.
Частной
производной по независимой переменной
![]() в точке
в точке
![]() от функции
от функции
![]() называется предел (если существует)
отношения частного приращения
называется предел (если существует)
отношения частного приращения![]() функции к приращению
функции к приращению![]() переменной
переменной![]() при стремлении
при стремлении![]() к нулю:
к нулю:
 .
.
Частную производную обозначают одним из символов:
![]() ;
;![]() .
.
Замечание.
Индекс
![]() внизу в этих обозначениях лишь указывает,
по какой из переменных берется производная,
и не связана с тем, в какой точке
внизу в этих обозначениях лишь указывает,
по какой из переменных берется производная,
и не связана с тем, в какой точке![]() эта производная вычисляется.
эта производная вычисляется.
Вычисление частных производных не представляет ничего нового по сравнению с вычислением обыкновенной производной, необходимо только помнить, что при дифференцировании функции по какой-либо переменной все остальные переменные принимаются за постоянные. Покажем это на примерах.
Пример
1. Найти
частные производные функции
![]() .
.
Решение.
При вычислении частной производной
функции
![]() по аргументу
по аргументу![]() рассматриваем функцию
рассматриваем функцию![]() как функцию только одной переменной
как функцию только одной переменной![]() ,
т.е. считаем, что
,
т.е. считаем, что![]() имеет фиксированное значение. При
фиксированном
имеет фиксированное значение. При
фиксированном![]() функция
функция![]() является степенной функцией аргумента
является степенной функцией аргумента![]() .
По формуле дифференцирования степенной
функции получаем:
.
По формуле дифференцирования степенной
функции получаем:
![]()
![]()
Аналогично,
при вычислении частной производной
![]() считаем, что фиксировано значение
считаем, что фиксировано значение![]() ,
и рассматриваем функцию
,
и рассматриваем функцию![]() как показательную функцию аргумента
как показательную функцию аргумента![]() .
В итоге получаем:
.
В итоге получаем:
![]()
Пример
2. Найти
частные производные
![]() и
и![]() функции
функции![]() .
.
Решение.
При вычислении частной производной по
![]() заданную функцию
заданную функцию![]() мы будем рассматривать как функцию
одной переменной
мы будем рассматривать как функцию
одной переменной![]() ,
а выражения, содержащие
,
а выражения, содержащие![]() ,
будут постоянными множителями, т.е.
,
будут постоянными множителями, т.е.![]() выступает в роли постоянного коэффициента
выступает в роли постоянного коэффициента![]() при степенной функции
при степенной функции![]() (
(![]() ). Дифференцируя
это выражение по
). Дифференцируя
это выражение по
![]() ,
получим:
,
получим:![]()
![]() .
.
Теперь,
наоборот, функцию
![]() рассматриваем как функцию одной
переменной
рассматриваем как функцию одной
переменной![]() ,
в то время как выражения, содержащие
,
в то время как выражения, содержащие![]() ,
выступают в роли коэффициента
,
выступают в роли коэффициента![]() (
(![]() ).Дифференцируя
).Дифференцируя
![]() по правилам дифференцирования
тригонометрических функций, получаем:
по правилам дифференцирования
тригонометрических функций, получаем:
![]()
Пример
3. Вычислить
частные производные функции
![]() в точке
в точке![]() .
.
Решение.
Находим сначала частные производные
данной функции в произвольной точке
![]() её области определения. При вычислении
частной производной по
её области определения. При вычислении
частной производной по![]() считаем, что
считаем, что![]() являются постоянными.
являются постоянными.
![]()
при
дифференцировании по
![]() постоянными будут
постоянными будут![]() :
:
![]()
а
при вычислении частных производных по
![]() и по
и по![]() ,
аналогично, постоянными будут,
соответственно,
,
аналогично, постоянными будут,
соответственно,![]() и
и![]() ,
т.е.:
,
т.е.:
![]()
Теперь
вычислим значения этих производных в
точке
![]() ,
подставляя в их выражения конкретные
значения переменных. В итоге получаем:
,
подставляя в их выражения конкретные
значения переменных. В итоге получаем:

11. Частные и полный дифференциалы функции
Если теперь к частному
приращению
![]() применить теорему Лагранжа о конечных
приращениях по переменной
применить теорему Лагранжа о конечных
приращениях по переменной![]() ,
то, считая
,
то, считая![]() непрерывной, получим следующие
соотношения:
непрерывной, получим следующие
соотношения:

где
![]() ,
,
![]() – бесконечно малая величина.
– бесконечно малая величина.
Частным
дифференциалом функции
![]() по переменной
по переменной![]() называется главная линейная часть
частного приращения
называется главная линейная часть
частного приращения![]() ,
равная произведению частной производной
по этой переменной на приращение этой
переменной, и обозначается
,
равная произведению частной производной
по этой переменной на приращение этой
переменной, и обозначается
![]()
Очевидно, частный дифференциал отличается от частного приращения на бесконечно малую высшего порядка.
Полным приращением функции многих переменных называется то её приращение, которое она получит, когда мы всем независимым переменным дадим приращение, т.е.
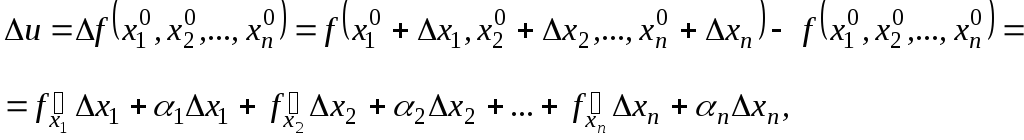
где
все
![]() ,
зависят от
,
зависят от![]() и вместе с ними стремятся к нулю.
и вместе с ними стремятся к нулю.
Под
дифференциалами
независимых переменных
![]() условились подразумеватьпроизвольные
приращения
условились подразумеватьпроизвольные
приращения
![]() и обозначать их
и обозначать их![]() .
Таким образом, выражение частного
дифференциала примет вид:
.
Таким образом, выражение частного
дифференциала примет вид:
![]()
Например,
частный дифференциал
![]() по
по![]() определяется так:
определяется так:
![]() .
.
Полным
дифференциалом
![]() функции многих переменных
функции многих переменных![]() называется главная линейная часть
полного приращения
называется главная линейная часть
полного приращения![]() ,
равная
,
равная![]() ,
т.е.сумме
всех её частных дифференциалов:
,
т.е.сумме
всех её частных дифференциалов:
![]()
Если
функция ![]() имеет непрерывные частные производные
имеет непрерывные частные производные
![]()
в
точке
![]() ,
то онадифференцируема
в данной точке.
,
то онадифференцируема
в данной точке.
При достаточно малом
![]() для дифференцируемой функции
для дифференцируемой функции![]() имеют место приближенные равенства
имеют место приближенные равенства
![]() ,
,
![]() ,
,
с помощью которых можно производить приближенные вычисления.
Пример
4. Найти
полный дифференциал функции
![]() трёх переменных
трёх переменных![]() .
.
Решение. Прежде всего, находим частные производные:
![]()

![]()
Заметив, что они непрерывны при всех
значениях
![]() ,
находим:
,
находим:

![]()
![]()
Для дифференциалов функций
многих переменных верны все теоремы о
свойствах дифференциалов, доказанные
для случая функций одной переменной,
например: если
![]() и
и![]() – непрерывные функции переменных
– непрерывные функции переменных![]() ,
имеющие непрерывные частные производные
по всем переменным, а
,
имеющие непрерывные частные производные
по всем переменным, а![]() и
и![]() – произвольные постоянные, то:
– произвольные постоянные, то:
 (6)
(6)
