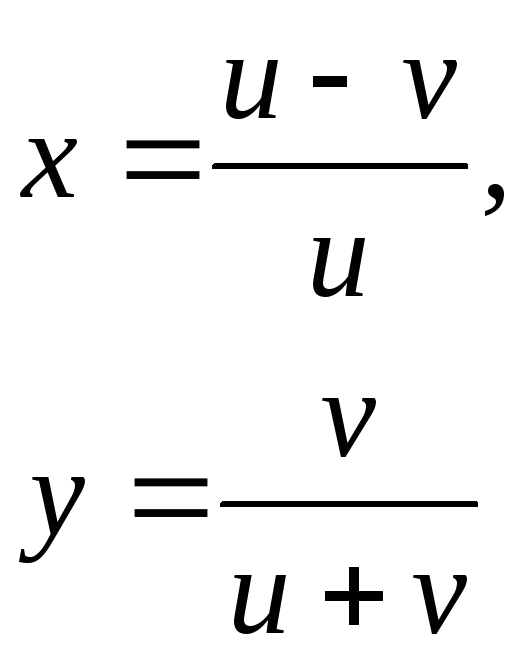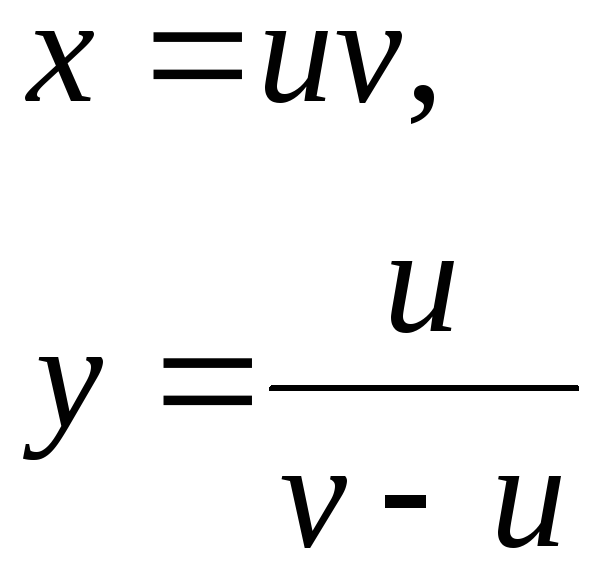- •Функции многих переменных типовые задания для самостоятельнОй работы
- •2. Найти частные производные и полные дифференциалы первого и второго порядков от функции
- •3. Найти указанные производные сложной функции и записать ее полный дифференциал
- •4. Найти частные производные и полные дифференциалы первого и второго порядка функции , заданной неявно
- •5. Вычислить градиент и производную функции по направлению вектора в точке . Записать уравнения касательной плоскости и нормали к поверхности, заданной уравнением , в точке
- •6. Исследовать функцию на экстремум
- •7. Исследовать функцию на условный экстремум при данных уравнениях связи
- •8. Найти наибольшее и наименьшее значения функции в области d, заданной системой неравенств
Функции многих переменных типовые задания для самостоятельнОй работы
-
Для функции z =ƒ(x‚y) указать область ее определения и область ее значений. Построить линии уровня поверхности, определенной этой функцией.
-
z = x2 - y2
-

-
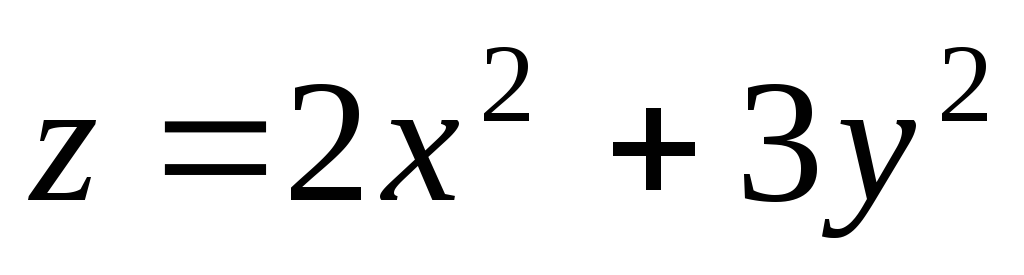
-
z = x - y2
-
z = x2 + y
-
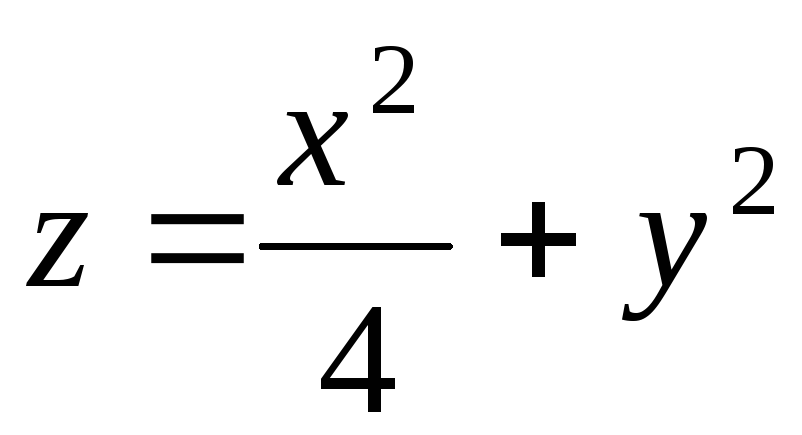
-
z = x2 - 3y2 + 5
-
z = x2 + 2x + y2 - 2y
-
z = 16x2 + 25y2
-
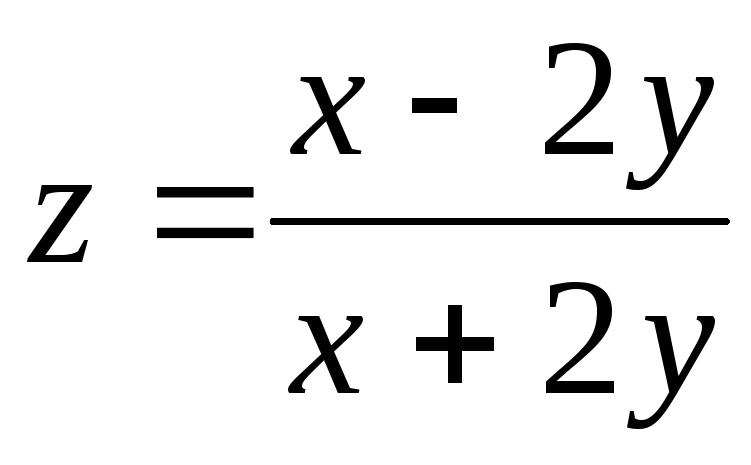
-
z = 25x2 - 16y2
-
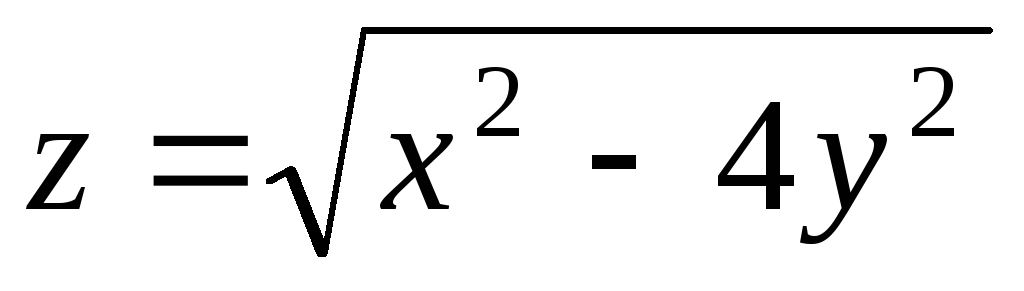
-
z = x - 3y - 8
-
z = x - 9y2
-
z = 2x2 – y
-
z = 16x2 – 25y2
-
z = x2 – 2x + y2 + 2y
-
z = 5x – 3y + 2
-
z = x2 + 4x – y2
-
z = 4x2 + 16x – y2 – 8y
-
z = x + y2
-

-
z = 49x2 + 9y2
-
z = x2 – y2 – 4y
-
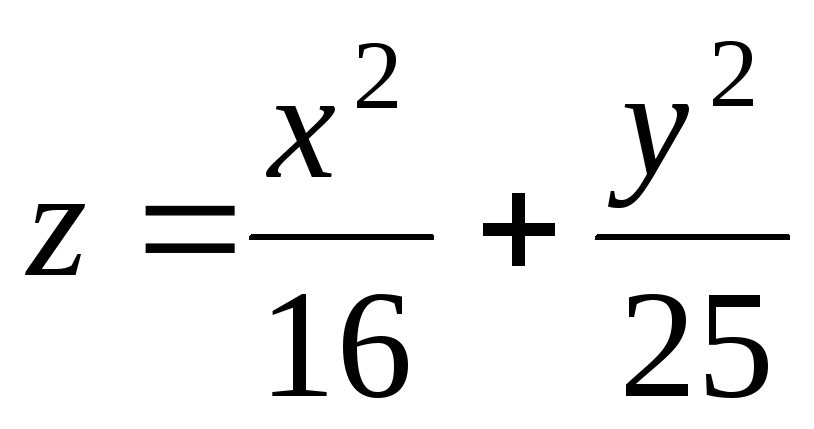
-
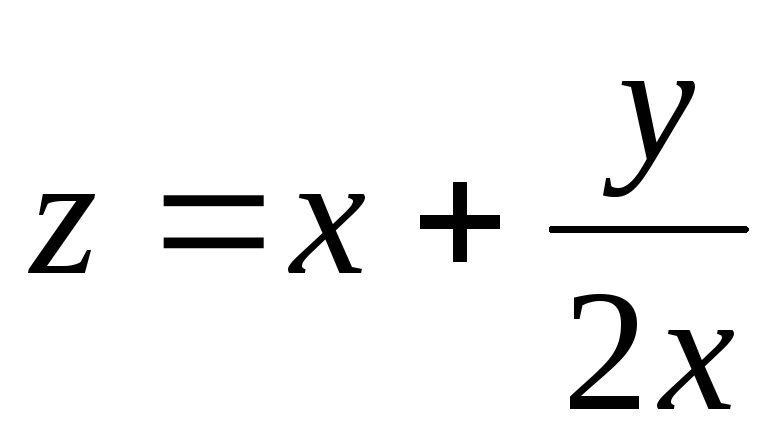
-
z = 4x2 – y2 – 8y
-
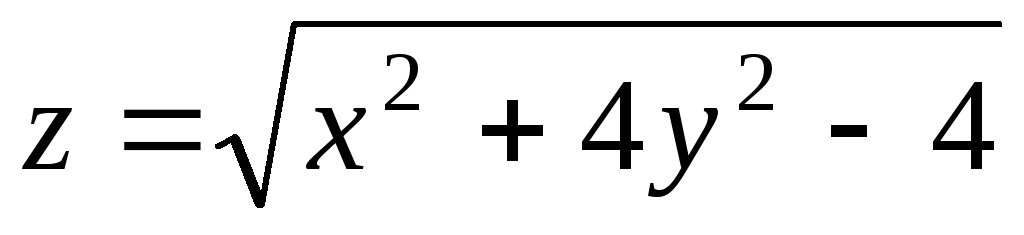
-
z = x2 + 2x – 4y2
-
z = 2x2 – 4y2 + 5
2. Найти частные производные и полные дифференциалы первого и второго порядков от функции
-
1.
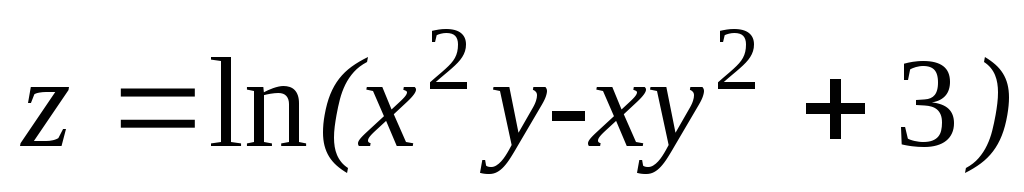
2.
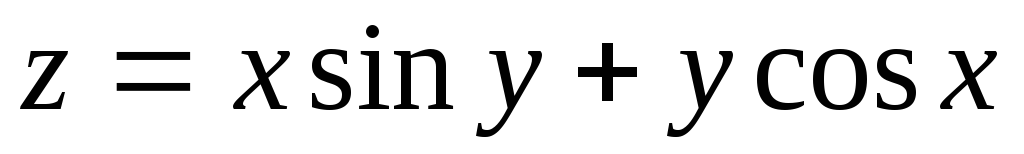
3.
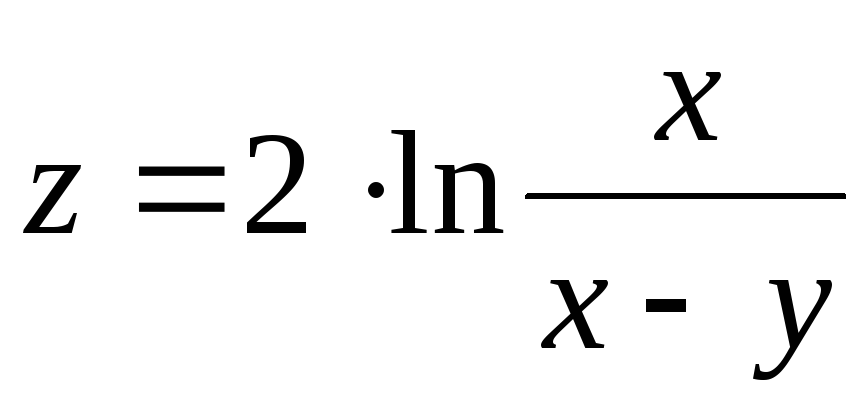
4.

5.
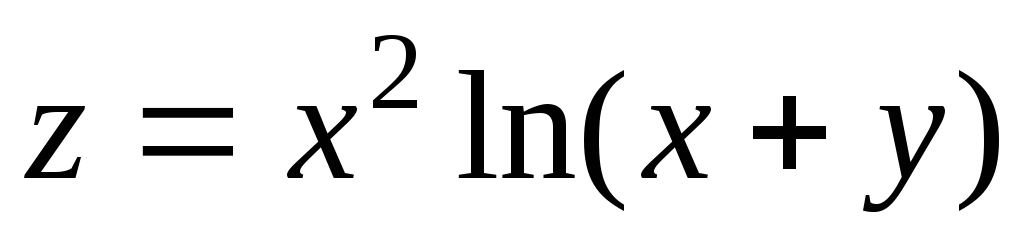
6.
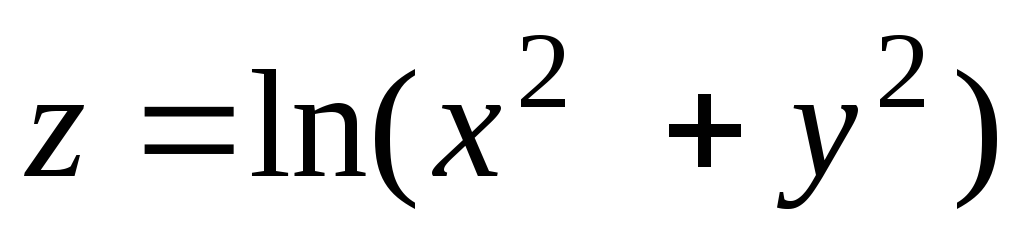
7.

8.
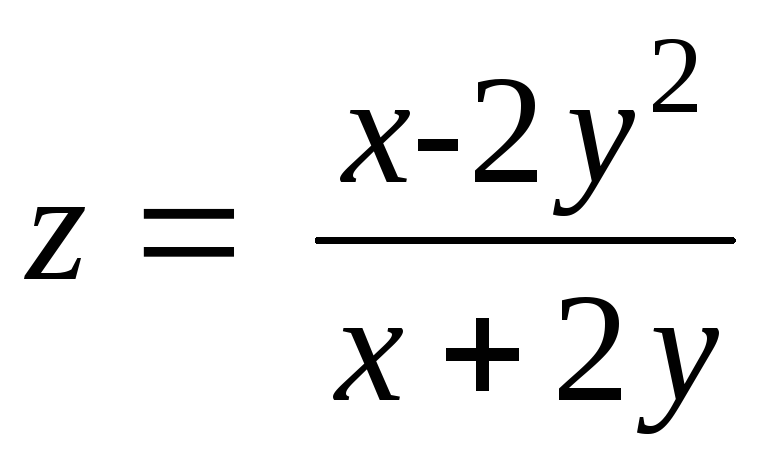
9.
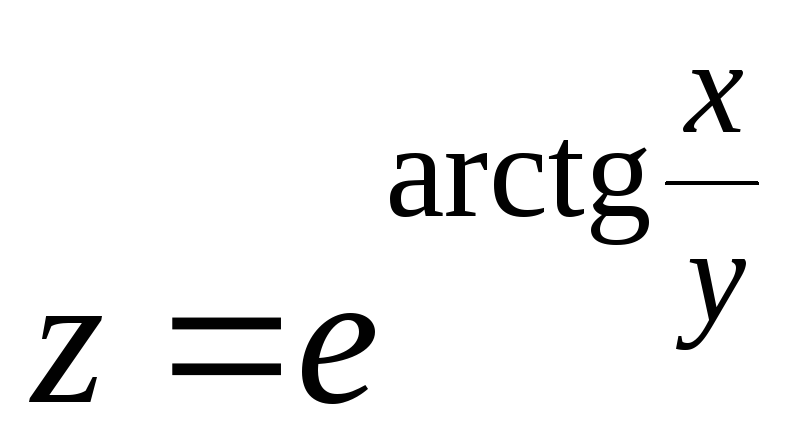
10.
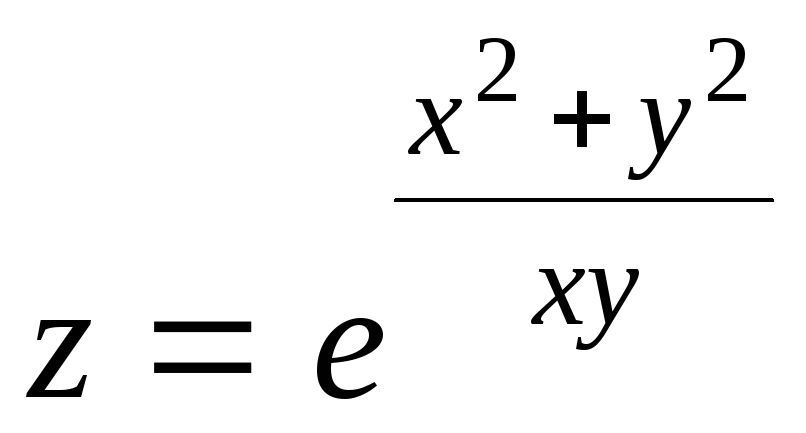
11.
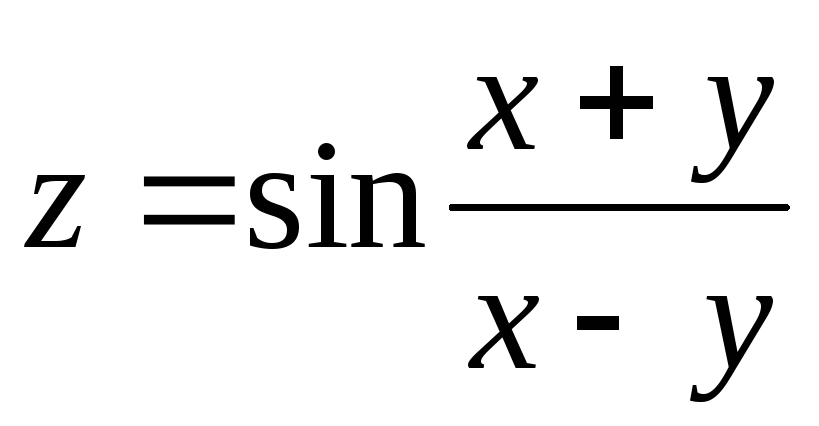
12.

13.
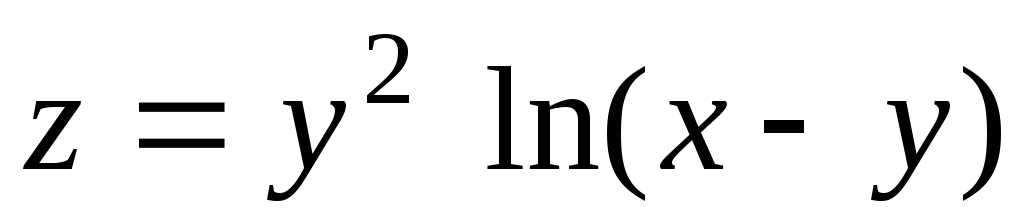
14.

15.
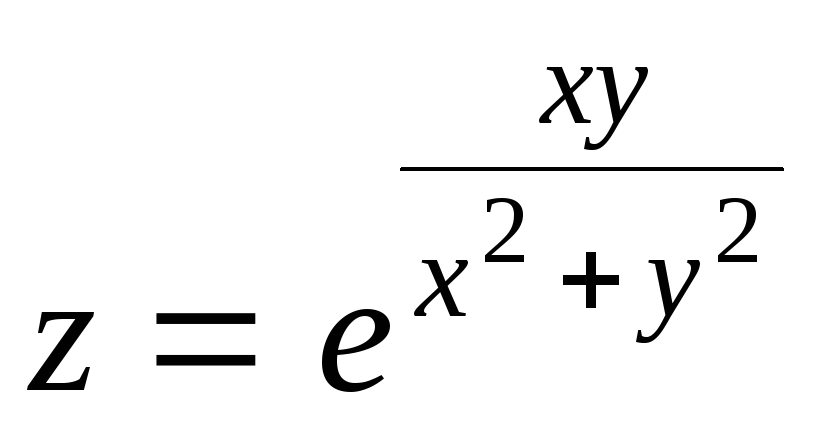
16.
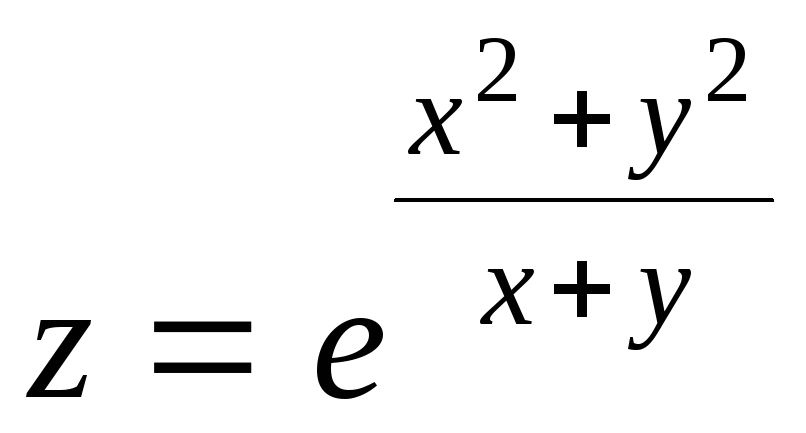
17.
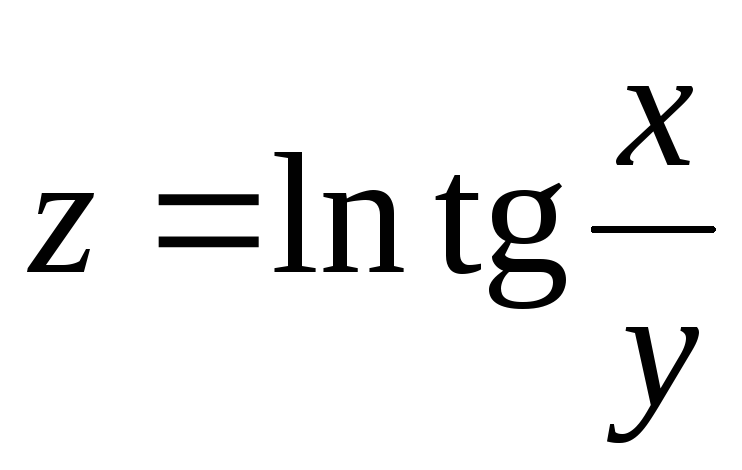
18.
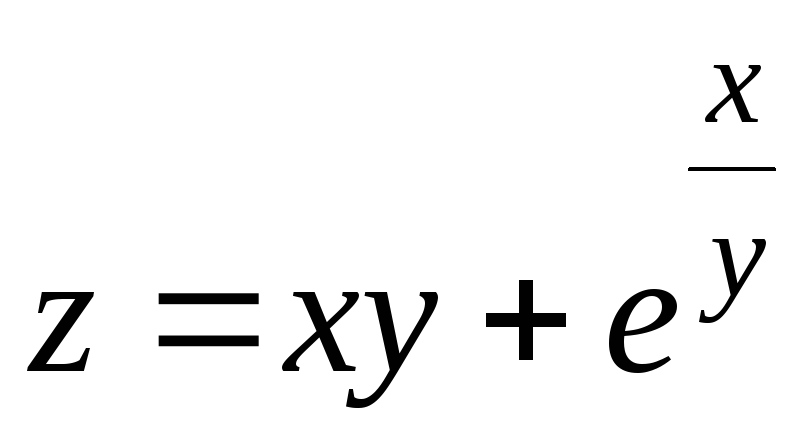
19.
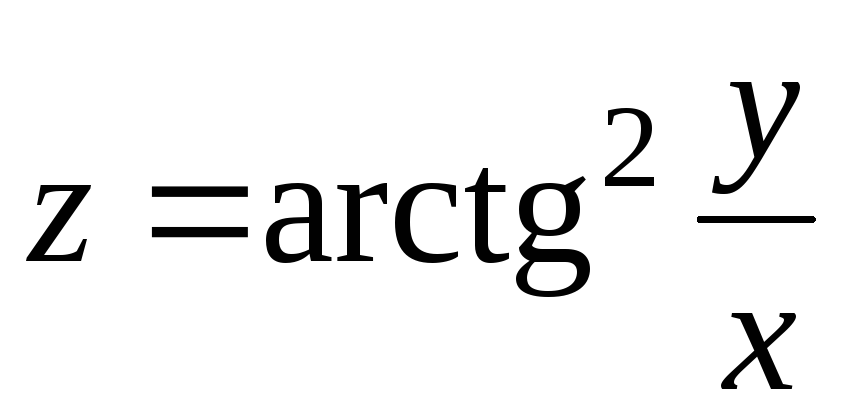
20.
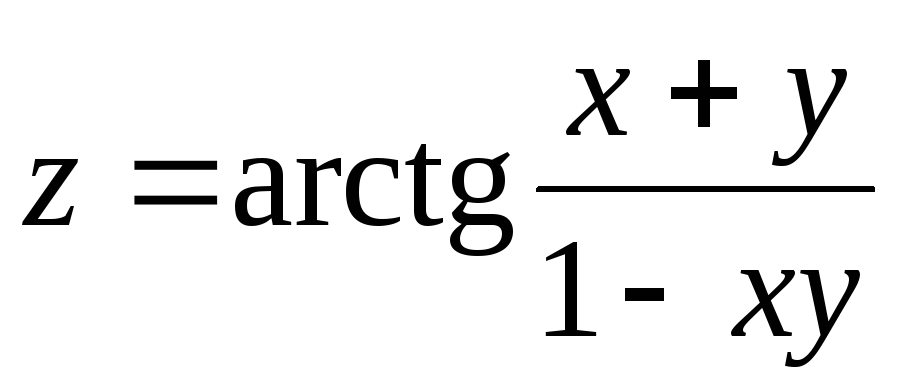
21.
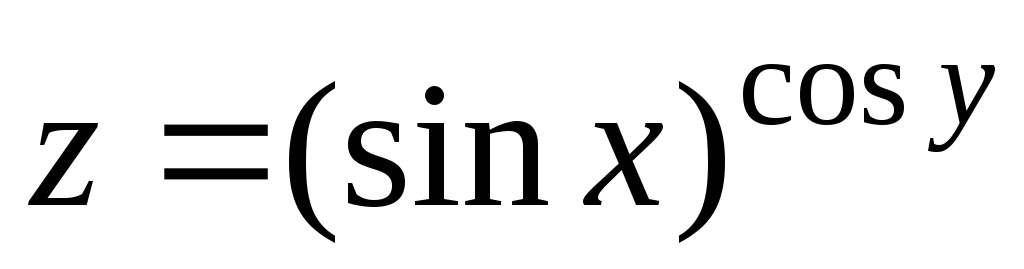
22.
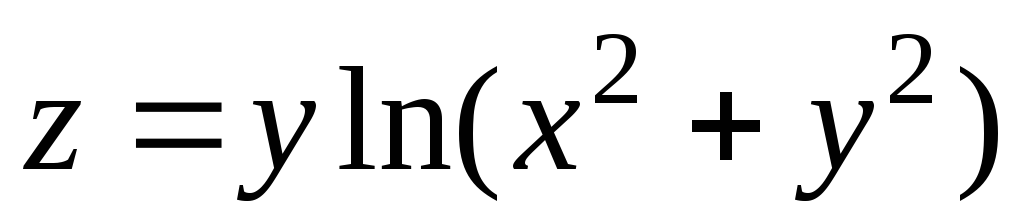
23.

24.

25.
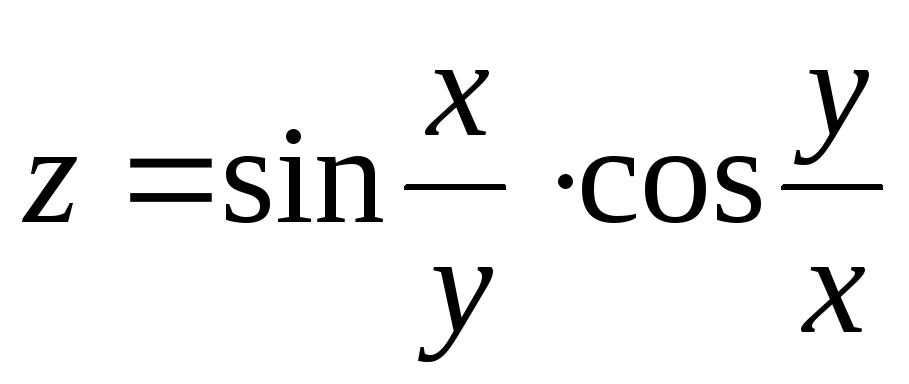
26.
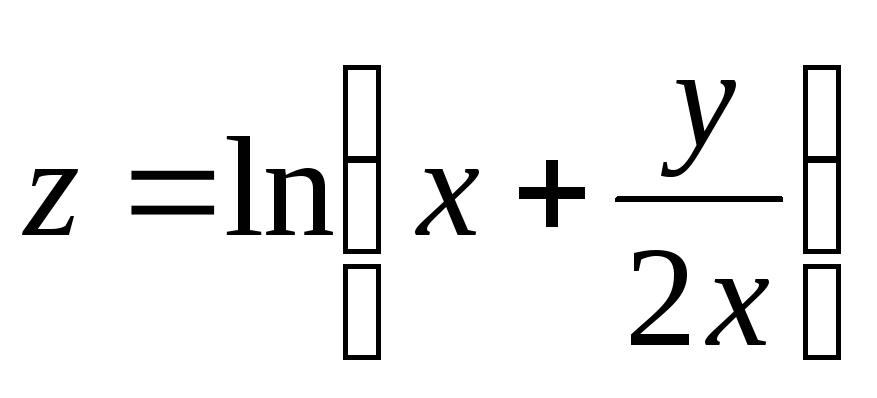
27.

28.

29.
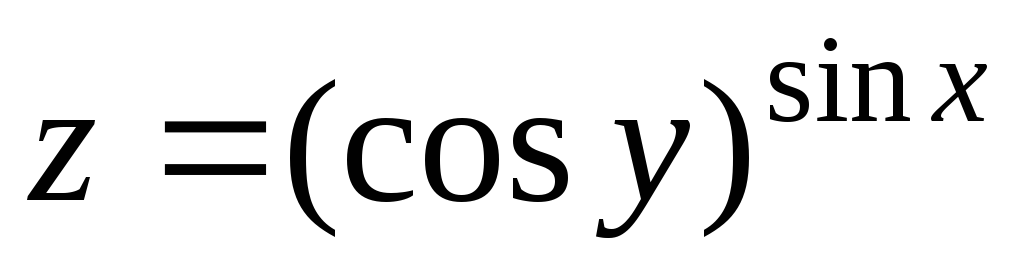
30.
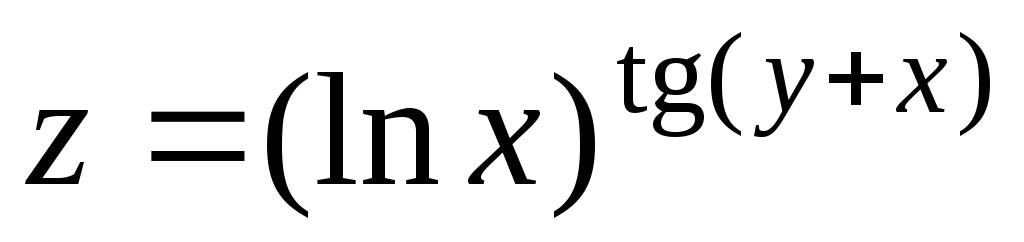
3. Найти указанные производные сложной функции и записать ее полный дифференциал
|
|
|
|
Найти |
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
|
10. |
|
|
|
|
11. |
|
|
|
|
12. |
|
|
|
|
13. |
|
|
|
|
14. |
|
|
|
|
15. |
|
|
|
|
16. |
|
|
|
|
17. |
|
|
|
|
18. |
|
|
|
|
19. |
|
|
|
|
20. |
|
|
|
|
21. |
|
|
|
|
22. |
|
|
|
|
23. |
|
|
|
|
24. |
|
|
|
|
25. |
|
|
|
|
26. |
|
|
|
|
27. |
|
|
|
|
28. |
|
|
|
|
29. |
|
|
|
|
30. |
|
|
|